Стоячі хвилі

Особливим випадком інтерференції є стоячі хвилі, тобто хвилі, що утворюються при накладенні двох біжучих хвиль, що розповсюджуються назустріч одна одній з однаковими частотами і амплітудами, а у разі поперечних хвиль – і однаковою поляризацией.

Нехай дві плоскі хвилі розповсюджуються назустріч одна одній уздовж осі х в середовищі без загасання, причому обидві хвилі характеризуються однаковими амплітудами і частотами. Крім того, початок координат виберемо в точці, в якій обидві хвилі мають однакову початкову фазу, а відлік часу почнемо з моменту, коли початкові фази обох хвиль дорівнюють нулю. Тоді відповідно рівняння хвилі, що розповсюджується уздовж позитивного напряму осі х, і хвилі, що розповсюджується їй назустріч, матимуть вигляд

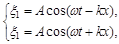
Склавши ці рівняння і врахувавши, що 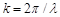, отримаємо рівняння стоячої хвилі:

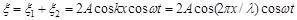з якого витікає, що в кожній точці цієї хвилі відбуваються коливання тієї ж самої частоти 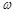з амплітудою 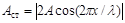, яка залежить від координати х точки, що розглядається.

В точках середовища, де

амплітуда результуючого коливання досягає свого максимального значення, якедорівнює .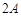

В точках середовища, де

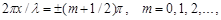
амплітуда результуючого коливання дорівнює нулю.

Зазначимо, що точки, в яких амплітуда коливань максимальна 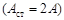, називаються пучностями стоячої хвилі, а точки, в яких амплітуда коливань дорівнює нулю 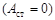, називаються вузлами стоячої хвилі. Точки середовища, що знаходяться в вузлах, не коливаються.

Координати пучностей та координати вузлів неважко отримати з двох останніх виразів:

З цих виразів витікає, що відстань пучність – пучність дорівнює 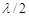, а відстань пучність – вузол дорівнює .

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Інтерференція хвиль	\|	ЗАБЕЗПЕЧЕННЯ ЖД.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.013 сек.