• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Інтерференція хвиль

Лекція 19

1. Інтерференція хвиль. Умови виникнення максимумів та мінімумів інтерференції. Оптична довжина шляху, оптична різниця ходу

Узгоджене протікання в часі і просторі декількох коливальних або хвильових процесів пов'язують з поняттям когерентності.

Когерентні хвилі – це хвилі, у яких різниця їх фаз залишається постійною в часі. Такими хвилями можуть бути лише хвилі, що мають однакову частоту, тобто цій умові задовольняють монохроматичні хвилі, тобто хвилі, які необмежені в просторі і мають лише одну визначену і строго постійну частоту.

Зазначимо, що жодне реальне джерело не дає строго монохроматичного світла. Тому хвилі, що випромінюються будь-яким незалежним джерелом світла, завжди некогерентні.

Розглянемо накладення двох когерентних хвиль.

Явище накладення в просторі двох (або декількох) когерентних хвиль в різних точках цього простору, при якому відбувається посилення або ослаблення результуючої хвилі – залежно від співвідношення між фазами цих хвиль називається інтерференцією хвиль.

Розглянемо накладення двох когерентних сферичних хвиль 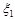і 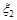, тобто хвиль, хвильові поверхні яких мають вид концентричних сфер, які збуджуються точковими джерелами і 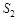(рис. 19.1), що коливаються з однаковими амплітудою 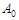і частотою 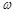і постійною різницею фаз:

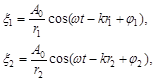
де і 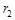– відстані від джерел хвиль до точки В , що розглядається; 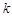– хвильове число; 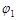і 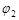– початкові фази обох сферичних хвиль, що накладаються.

Рис. 19.1

Квадрат амплітуди результуючої хвилі в точці В дорівнює:

.

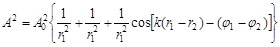Оскільки для когерентних джерел різниця початкових фаз 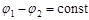, результат накладення двох хвиль в різних точках залежить від величини 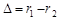, яка називається різницею ходу хвиль.

В точках, де

(*)

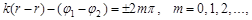спостерігається інтерференційний максимум: амплітуда результуючого коливання .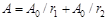

В точках, де

(**)

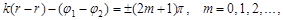спостерігається інтерференційний мінімум: амплітуда результуючого коливання .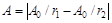

Величина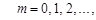називається відповідно порядком інтерференційного максимума або мінімума.

Умови (*) і (**) зводяться до того, що

.

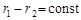Це рівнянням гіперболи з фокусами в точках і 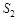. Отже, геометричне місце точок, в яких спостерігається посилення або послаблення результуючого коливання, є сімейством гіпербол (рис. 19.1), що відповідають умові 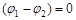. Між двома інтерференційними максимумами (на рис. 19.1 суцільні лінії) знаходяться інтерференційні мінімуми (на рис. 19.1 штрихові лінії).

Читайте також:

1. Адаптивні хвилькові перетворення : Хвилькові пакети.
2. АЧТ-це тіло, поглинальна здатність якого (для всіх довжин хвиль) тотожне 1.
3. Геометрична та хвильова оптика.
4. Групова швидкість і дисперсія хвиль
5. Довжиною хвилі є відстань, на яку поширюється хвильовий процес за час одного періоду коливань.
6. Економічні цикли та їх фази. Теорія «довгих хвиль» в економіці.
7. Електромагнітні хвилі. Шкала електромагнітних хвиль
8. Енергія електромагнітних хвиль. Вектор Умова-Пойнтінга
9. Зв'язок в мікрохвильовому діапазоні
10. Зв'язок між зоровим сприйняттям довгих хвиль і суб’єктивним відчуттям світла
11. Землетруси – це раптове звільнення потенціальної енергії земних надр, яка у вигляді ударних хвиль та пружних коливань (сейсмічні хвилі) розповсюджується в землі у всіх напрямках
12. Інтерференція світла

Переглядів: 4053