Наведемо декілька рикладів побудови моделей.

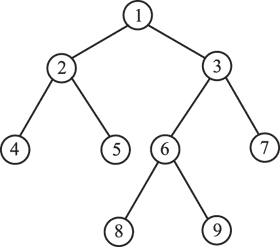
Рис. 15.2. Ієрархічна модель

Рис.15.1

Модель і моделювання – універсальні поняття , атрибути одного із найбільш потужних методів познання в будь-якій професійный галузі.

Не існує загальної теорії побудови моделей. Побудова моделі – системна задача, що потребує аналіза і сінтеза початкових даних, гіпотез, теорій, знань спеціалістів. Системний підхід не тільки дозволяє побудувати модель реальної системи, але й використати її для оцінки системи, наприклад, для оцінки ефективності управління та функціонування.

Яскравими прикладами системного підходу (широкого охоплення фактів та їх детального аналізу) насичені праці В.І. Вернадського, який першим встановив єдність органічної та неорганічної природи і необхідність вивчення біосфери як єдиного комплексу.

Сьогодні проблеми взаємодії людини і біосфери вкрай актуальні. Математики та ІТ-спеціалісти у вивченні цих процесів відіграють не меншу роль, ніж в еволюції фізики та техніки. Організація таких досліджень надзвичайно складна, оскільки потребує участі спеціалістів різних галузей, які говорять на різних "професійних мовах". Система формальних моделей може стати єдиним інтерпретатором, здатним створити "загальну мову", сформулювати вимоги до інформації і, врешті-решт, бути архітектором тих систем, що стануть скелетом міждисциплінарного характеру.

Означений підхід носить загальний характер. Тріумф молекулярної біології в останні роки, успіхи у дослідженні генетичного коду, моделювання окремих функцій людського організму, роботизація, пошуки в галузі штучного інтелекту, макро- і мікроекономічні системи — усе це досягнення галузевих наук методами системного підходу та інформаційних технологій.

Поки що йшлося про природничі науки. А як виглядають справи в гуманітарних і соціальних науках, де вольовий людський фактор має суттєвий вплив і погано піддається формалізації?

Плутанина і суперечності, характерні для широкого спектра неприродничих наук, дають всі підстави стверджувати, що процеси в цих науках також повинні розглядатись як "складні системи" з відповідними інформаційними моделями.

Хід будь-якого суспільного процесу залежить тією чи іншою мірою від людей, від їх поведінки і рішень. Але дії людей, врешті-решт, не такі вже довільні, ніж це може здаватися, і мотивація цих дій лежить у матеріальній єдності життя. Видатний фізик-теоретик Е. Шредінгер у своїй книжці "Що таке життя з точки зору фізики" дійшов висновку, що найбільшу ймовірність реалізації має той процес, який є найбільш економічним з погляду енергетики. Такими процесами є стабільні процеси. Саме тому прагнення зберегти стабільність свого колективу, фірми, свого класу, національної спільноти є однією з найпотужніших пружин, що підтримують функціонування механізму суспільної еволюції.

Це класичні системи зі зворотними зв'язками і визначеною цільовою функцією. Незважаючи на великі труднощі врахування "вольового фактору", такі системи, як і суто фізичні, піддаються моделюванню з різними траєкторіями перебігу процесу залежно від цього самого вольового впливу. Для цього вже існують і розвиваються математична теорія ігор, теорія розпізнавання, системна динаміка та ін. Враховуючи світові тенденції до інтеграції та глобалізації, можна припустити, що в майбутньому суспільні системи будуть тільки ускладнюватись, і їх "математизація" є єдиною альтернативою більш-менш оптимального розвитку.

У цьому коротенькому огляді зроблено акцент лише на одній думці: на людство звалилася така злива інформації, а об'єкти досліджень стали настільки складними, що одного життя людини вже не вистачає для засвоєння накопичених пращурами знань, а тим більше для їх поглиблення. Потрібен невмирущий "машинний" розум у вигляді баз даних, баз знань, моделей об'єктів і процесів. Поки що це не абсолют, а лише тенденція, але тенденція з усіх без винятку сферах людської діяльності, і тільки той досягне успіху, хто "впишеться" в цю тенденцію.

Модель – це відображення фізичної системи (объекта) на математичну систему, наприклад, математичний аппарат рівнянь. Будь-яка модель створюється і досліджується при певних припущеннях, гипотезах.

Приклад.Розглянемо фізичну систему: тіло масою m, на яке діє сила F, скочується нахиленою площиною з прискоренням а. Досліджуя такі системи, Н’ютон одержав математичне відношення: F=ma. Це математична модель фізичної системи. При опису цієї системи (побудові цієї моделі) були зробленні наступні припущення: 1) поверхня ідеальна (тобто коеф іцієнт тертя дорівнює нулю); 2) тіло знаходиться у вакумі ( тобто опір повітря дорівнює нулю); 3) маса тіла незмінна; 4) тіло рухається з однаковим постійним прискоренням в будь- якій точці.

Класифікацію моделей проводять по різним критеріям. Ми будемо використовувати найбільш просту і практичну класифікацію.

Модель називається статичною, якщо серед параметрів, що приймають учать в її описі, немає часового параметру.

Модель динамічна, якщо серед її параметрів є часовий параметр, тобто вона відображає систему (процеси в системі) в часі.

Приклад. Модель 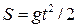- динамічна модель шляху при вільному падіння тіла.

Модель дискретна, якщо вона описує поведінку системи в дискретні моменти часу.

Приклад. Якщо розглядати рух тільки в моменти , то модель 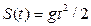чи часова послідовність S₀=0, S₁=g/2, S₂=2g, S₃=9g/2, :, S₁₀=50g може служити дискретною моделлю, вільно падаючого тіла.

Модель неперервна, якщо вона описує поведінку системи для всіх моментів часу з деякого проміжку часу.

Приклад. Модель 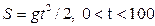неперервна в проміжку часу (0; 100).

Модель імітаційна, якщо вона призначена для випробовування або вивчення можливих напрямків розвитку та поведінки об’єкта через варіювання деяких чи всіх параметрів моделі.

Імітаційне моделювання – один з найбільш потужних інструментів аналізу, якими володіють люди, відповідальний за розробку і функціонування складних процесів і систем.

Всі імітаційні моделі являють собою моделі типу, так званого, «чорного ящика». Це означає, що вони забезпечують видачу вихідного сигналу системи в тому разі, коли на її підсистеми поступає вхідний сигнал. Тому для одержання результатів необхідно здійснити «прогон» імітаційних моделей, а не «вирішувати» їх. Імітаційні моделі не здатні формувати своє рішення у тому вигляді, в якому це має місце в аналітичних моделях, а можуть лише служити як засіб для аналізу поведінки системи в умовах, які задаються експериментом. Таким чином, імітаційне моделювання – не теорія, а методологія вирішення проблем.

Модель детермінована, якщо кожному набору параметрів відповідає цілком визначений і однозначний набір вихідних параметрів; в протилежному випадку – модель не детермінована, стохастатична.

Модель функціональна, якщо її можна представити у вигляді системи деяких функціональних відношень. Наприклад , .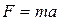

Модель логічна, якщо вона представлена логічними функціями. Наприклад, однорозрядний суматор може бути відображений такими рівняннями: Σ = xy v xy, с = xy

Модель алгоритмічна, якщо вона описана алгоритмом чи комплексом алгоритмів, що визначають її функціонування.

Модель структурна, якщо вона представлена наприклад, структурою даних і відношеннями між ними.

Модель ієрархічна (деревоподібна), якщо представлена якоюсь ієрархічною структурою (деревом). (Рис .15.2)

Модель мережева, якщо вона представлена мереженою структурою, наприклад локальною мережею з’єднання, комп’ютерів.

Модель натурна, якщо вона є матеріальною копією об’єкта моделювання, наприклад глобус, як модель земної кулі.

Тип моделі залежать від інформативної сутності моделюючої системи, від зв’язків і відношень між її підсистемами і елементів, а не від фізичної природи. Границі між моделями різного типу досить умовні. Скоріше можемо говорити про різні режими використання моделей – функціональний, імітаційний, стахостатичний і т.д.

Основні властивості будь-якої моделі:

· цілеспрямованість – модель завжди відображує якусь систему, тобто має певну ціль;

· спрощеність – модель відображає тільки суттєві сторони об’єкта і, крім того, повинна бути простою для дослідження і відтворення;

· адекватність – модель повинна успішно описувати моделюючу систему в рамках цільової орієнтації;

· інформативність – модель повинна містити достатню інформацію про систему (в рамках гіпотез, що прийняті при створенні моделі) і повинна надавати можливість одержувати нову інформацію;

· повнота – в моделі повинні бути передбачені всі основні зв’язки і відношення, необхідні для забезпечення цілі моделювання.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
	\|

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.