Показники вирощування сільськогосподарських культур

Показник (із розрахунку на 1 га)	Озима пшениця	Цукрові буряки	Наявний ресурс
Затрати праці, людино-днів
Затрати праці механізаторів, людино-днів
Урожайність, тонн	3,5		—
Прибуток, тис. грн	0,7		—

Критерієм оптимальності є максимізація прибутку.

Нехай:

х₁ – шукана площа посіву озимої пшениці, га;

х₂– шукана площа посіву цукрових буряків, га.

Задача лінійного програмування:

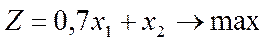(8)

за умов:

x₁ + x₂ ≤ 20; (9)

5x₁ + 25x₂ ≤ 270; (10)

2x₁ + 8x₂ ≤ 80; (11)

x₂ ≥ 5; (12)

x₁ ≥ 0, x₂ ≥ 0. (13)

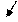
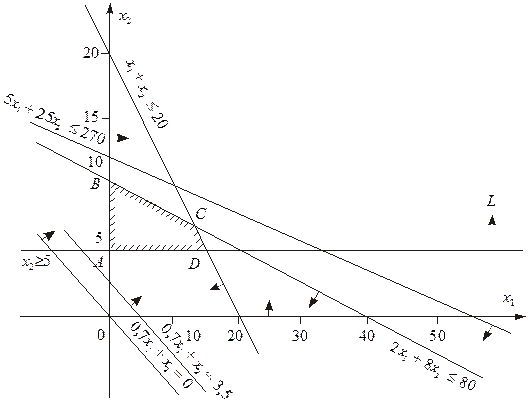
Рис. 2. Область допустимих розв’язків задачі

4. Основні властивості розв’язків задачі лінійного програмування

Властивість 1. Множина всіх планів задачі лінійного програмування опукла.

Властивість 2. Якщо ЗЛП має оптимальний план, то екстремального значення цільова функція набуває в одній із вершин її багатогранника розв’язків. Якщо ж цільова функція набуває екстремального значення більш як в одній вершині цього багатогранника, то вона досягає його і в будь-якій точці, що є лінійною комбінацією таких вершин.

Властивість 3. Якщо відомо, що система векторів A₁,A₂,…,A_k (k ≤ n) у розкладі A₁x₁ +A₂x₂ + … + A_nx_n = A₀, X ≥ 0 лінійно незалежна і така, що A₁x₁ + A₂x₂ + … + A_kx_k = A₀, де всі x_j≥0, то точка X=(x₁,x₂,…,x_k,0,…,0) є кутовою точкою багатогранника розв’язків.

Властивість 4. Якщо X=(x₁,x₂,…,x_n) – кутова точка багатогранника розв’язків, то вектори в розкладі A₁x₁+A₂x₂+…+A_nx_n=A₀, X ≥ 0, що відповідають додатним x_j, є лінійно незалежними.

Отже, якщо цільова функція ЗЛП обмежена на багатограннику розв’язків, то:

1) існує така кутова точка багатогранника розв’язків, в якій цільова функція ЗЛП досягає свого оптимального значення;

2) кожний опорний план відповідає кутовій точці багатогранника розв’язків.

Тому для розв’язання задачі лінійного програмування необхідно досліджувати лише кутові точки багатогранника (опорні плани), не включаючи до розгляду внутрішні точки множини допустимих планів.

5. Графічний метод розв’язування ЗЛП

Задача. Знайти екстремум (максимум, мінімум) функції:

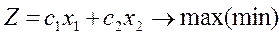(14)

за умов:

(15)

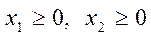. (16)

- система (15) за умов (16) сумісна і багатокутник її розв’язків обмежений.

Розв’язати ЗЛП графічно означає знайти таку вершину багатокутника розв’язків, у результаті підстановки координат якої в (14) лінійна цільова функція набуває найбільшого (найменшого) значення.

Алгоритм графічного методу розв’язування ЗЛП:

1. Будуємо прямі, рівняння яких дістаємо заміною в обмеженнях задачі (15) знаків нерівностей на знаки рівностей.

2. Визначаємо півплощини, що відповідають кожному обмеженню задачі.

3. Знаходимо багатокутник розв’язків ЗЛП.

4. Будуємо вектор 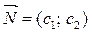, що задає напрям зростання значення цільової функції задачі.

5. Будуємо пряму с₁х₁+с₂х₂=const, перпендикулярну до вектора .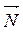

6. Рухаючи пряму с₁х₁+ с₂х₂ = const в напрямку вектора (для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину багатокутника розв’язків, де цільова функція набирає екстремального значення.

7. Визначаємо координати точки, в якій цільова функція набирає максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці.

Рис. 3 Рис. 4

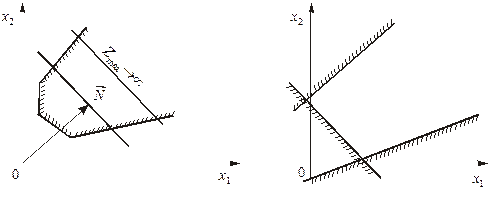
Рис. 5 Рис. 6

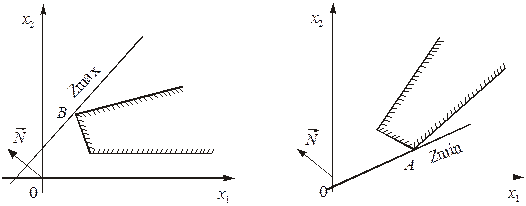
Рис. 7 Рис. 8

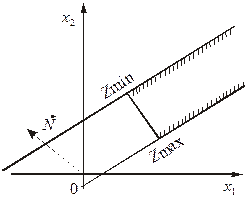
Рис. 9
Читайте також:
IV група- показники надійності підприємства
VI . Екзаменаційні питання з історії української культури
Абсолютні показники фінансової стійкості
Абсолютні показники фінансової стійкості та її типи
Абсолютні та відності показники результатів діяльності підприємства.
Агротехніка вирощування сіянців модрини
Агротехніка вирощування сіянців ялини
АДМІНІСТРАТИВНО-ПРАВОВЕ РЕГУЛЮВАННЯ У ГАЛУЗІ КУЛЬТУРИ
Амстердам, Дельфт — осередки культури Нідерландів
Аналітичні показники динаміки та прийоми їх обчислення
Аналітичні показники ряду динаміки.
Аналітичні показники ряду динаміки.

Переглядів: 738

<== попередня сторінка | наступна сторінка ==>

Форми запису задач лінійного програмування | Розв’язати графічним методом задачу лінійного програмування

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.