• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Форми запису задач лінійного програмування

Основні завдання сучасної вітчизняної соціології

У соціальній діяльності функції соціології взаємодіють, пронизуючи всі її сфери. Беручи до уваги їх розмаїття при вивченні й прогнозуванні суспільних процесів, можна окреслити найважливіші напрями досліджень сучасної вітчизняної соціології:

– вироблення спільно з іншими суспільствознавчими науками сучасної концепції побудови суспільства;

– цілісний соціологічний аналіз процесів перетворення суспільства у найширшому контексті (історичне минуле, сучасність, найближчі й віддалені перспективи);

– вивчення соціальної структури українського суспільства у її різноманітних вимірах (йдеться про реальну соціальну структуру, процеси стратифікації, формування за умов ринкових відносин нових соціальних груп і верств суспільства);

– вивчення національних проблем, процесів формування національної свідомості, відносин між різними націями і народностями;

– оптимізація соціальної політики в умовах переходу до ринкової економіки;

– вивчення мотивації трудової діяльності людей, її ціннісних орієнтацій та інтересів як важливих чинників політичних і економічних перетворень;

– аналіз проблем, пов´язаних з розвитком демократії, свободи слова, політичного плюралізму, зародження масових громадянських рухів;

– вивчення проблем формування громадської думки різних верств населення.

– за допомогою знака суми «S»:

за умов:

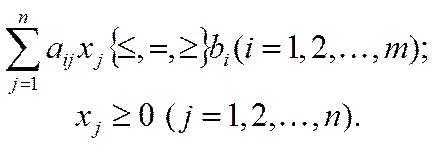(4)

– векторно-матричний вигляд:

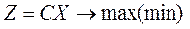
за умов: АХ А₀; (5)

Х ≥ 0,

де – матриця коефіцієнтів при змінних;

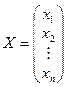– вектор змінних;

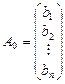– вектор вільних членів;

С = (с₁,с₂,…,с_п) – вектор коефіцієнтів при змінних у цільовій функції.

– векторна форма:

за умов:

A₁x₁ + A₂x₂ + … + A_nx_n 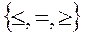A₀; (6)

X ≥0,

де

– вектори коефіцієнтів при змінних.

3. Геометрична інтерпретація задачі лінійного програмування

Розглянемо на площині х₁Оx₂ сумісну систему лінійних нерівностей:

(7)

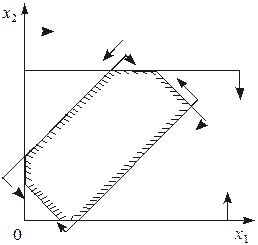Рис. 1.

Сукупність цих точок (розв’язків) називають багатокутником розв’язків, або областю допустимих планів (розв’язків) ЗЛП. Це може бути точка (єдиний розв’язок), відрізок, промінь, багатокутник, необмежена багатокутна область.

Якщо в системі обмежень (7) буде три змінних, то кожна нерівність геометрично визначатиме півпростір тривимірного простору, граничними площинами якого будуть
a_i1x₁ + a_i2x₂ + a_i3x₃ = b_i (i = 1, 2, ...,т), а умови
невід’ємності – півпростори з граничними площинами х_j = 0 (j = 1, 2, 3), де і – номер обмеження, а j – номер змінної.

Якщо система обмежень сумісна, то ці півпростори як опуклі множини, перетинаючись, утворять у тривимірному просторі спільну частину, що називається багатогранником розв’язків.

Якщо система обмежень сумісна, то за аналогією з тривимірним простором вона утворює спільну частину в n–вимірному просторі – опуклий багатогранник допустимих розв’язків.

Отже, геометрично ЗЛП являє собою відшукання координат такої точки багатогранника розв’яз­ків, при підстановці яких у цільову лінійну функцію остання набирає максимального (мінімального) значення, причому допустимими розв’язками є усі точки багатогранника розв’язків.

Цільову функцію

в п–вимірному просторі основних змінних можна геометрично інтерпретувати як сім’ю паралельних гіперплощин, положення кожної з яких визначається значенням параметра Z.

Приклад. Нехай фермер прийняв рішення вирощувати озиму пшеницю і цукрові буряки на площі 20 га, відвівши під цукрові буряки не менше як 5 га. Техніко-економічні показники вирощування цих культур маємо у табл. 1:

Таблиця 1

Читайте також:

1. А/. Форми здійснення народовладдя та види виборчих систем.
2. Автоматизовані форми та системи обліку.
3. Аграрні реформи та розвиток сільського госпо- дарства в 60-х роках XIX ст. — на початку XX ст.
4. Акредитив та його форми
5. Активні форми участі територіальної громади у вирішенні питань ММС
6. Алгоритм розв’язання задачі
7. Алгоритм розв’язання розподільної задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі
11. Алгоритм розв’язування задачі
12. Алгоритм розв’язування задачі

Переглядів: 1670