• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Проектувальний розрахунок

У розрахунковій формулі на стійкість

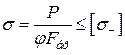, або ,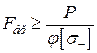

є дві невідомі величини — коефіцієнт φ та шукана площа брутто F_бр поперечного перерізу. Тому при доборі перерізів слід користуватися методом послідовних наближень, варіюючи значення коефіцієнта φ. Як пра­вило, в першій спробі беруть φ₁ = 0,5 ... 0,4. Вибираючи будь-яке з цих зна­чень φ₁, визначають потрібну площу F_бр та добирають переріз. Вибраний переріз перевіряють та визначають фактичне значення . Якщо знач­но відрізняється від φ₁ то й напруження відрізняється від допустимого. Тоді слід повторити розрахунок, тобто зробити другу спробу, взявши се­реднє за модулем значення між φ₁ та :

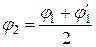. (4.18)

У результаті другої спроби визначають φ₂. Якщо потрібна третя спроба, то

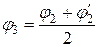
і т. д. Як правило, при доборі перерізів потрібно не більше ніж дві-три спроби.

Приклад. Доберемо за сортаментом двотавровий поперечний переріз стрижня завдовжки 5 м, що зазнає дії центрального стискального навантаження 320 кН. Оби­два кінці стрижня затиснуті. Матеріал – Ст3. Основне допустиме напруження [σ_–] =160 МПа.

Визначимо розрахункову зведену довжину стрижня:

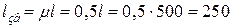см.

Добираємо поперечний переріз за методом послідовних наближень.

Перша спроба: вибираємо φ₁ = 0,5; потрібна площа поперечного перерізу

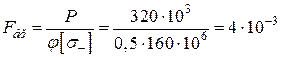м² = 40 см².

За сортаментом вибираємо двотавр № 27 з площею F = 40,2 см² та мінімальним раді­усом інерції i_тіп = i_ст = 2,54 см. Гнучкість стрижня

.

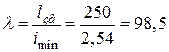За табл. 4.2 при лінійній інтерполяції

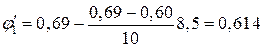»φ₁ = 0,4.

Перейдемо до другого наближення, взявши 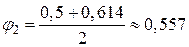. Потрібна пло­ща поперечного перерізу стрижня

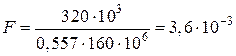м² = 36 см².

За сортаментом вибираємо двотавр № 24а з площею F = 37,5 см² та мінімальним ра­діусом інерції i_тіп = i_ст = 2,63 см. Гнучкість стрижня

.

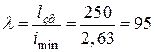За таблиці Е.1 (додаток Е) знаходимо коефіцієнт :

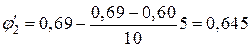»φ₂ = 0,557.

Переходимо до третього наближення, взявши

.

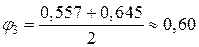Обчислюємо потрібну площу:

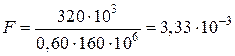м² = 33,3 см².

За сортаментом вибираємо двотавр № 24 з площею F = 34,8 см² та мінімальним раді­усом інерції i_тіп = i_ст = 2,37 см. Гнучкість стрижня

.

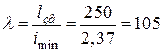Для λ=105 коефіцієнт

.

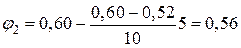Обчислимо напруження:

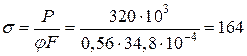МПа.

Перенапруження становить

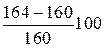% ≈ 2,5%.

Остаточно вибираємо для стрижня двотавр № 24.

Читайте також:

1. Автоматичний розрахунок суми проведення.
2. Аеродинамічний розрахунок
3. Аеродинамічний розрахунок ротора вітроустановки
4. Аналітичний розрахунок завантаження горловин
5. Аналітичний розрахунок сумарного завантаження типових перетинань
6. Види норм праці, їх розрахунок
7. Вплив характеру кола на криву струму при несинусоїдній напрузі /розрахунок найпростіших кіл
8. Гідравлічний розрахунок
9. Гідравлічний розрахунок малих мостів
10. Гідравлічний розрахунок сифонів
11. Графічний розрахунок режиму роботи ПСН
12. Графоаналітичний розрахунок витрат тепла і повітря на сушіння.

Переглядів: 640