• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник

Модифікація лінійних моделей

1. Метод штучного базису.

2. Двоїстий симплекс-метод.

3. Метод Гоморі.

1. Метод штучного базису

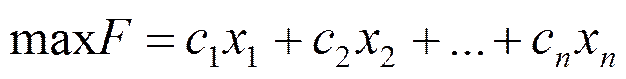(1)

(2)

(3)

Для отримання одиничної матриці необхідно до кожного рівняння в системі обмежень задачі додати одну змінну . Ці змінні називають штучними.

- (2) не містить жодного одиничного вектора:

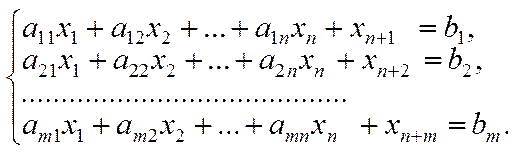(4)

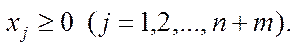
Задачу з системою обмежень (4) називають розширеною, або М-задачею.

У результаті процедур симплексних перетворень виключалися з базису штучні змінні – їх вводять у цільову функцію з від’ємними коефіцієнтами:

()

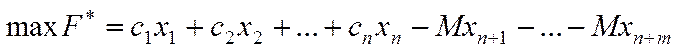
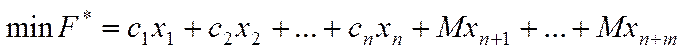- процедура симплексного методу одразу вилучає відповідні змінні з базису і забезпечує знаходження плану, в якому всі штучні змінні .

- якщо в оптимальному плані розширеної задачі існує хоча б одне значення 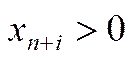, то це означає, що початкова задача не має розв’язку, тобто система обмежень несумісна.

- у таблиці оцінкові рядки поділені на дві частини-рядки: (m+2)-му рядку записують коефіцієнти з М,

(m+1)-му — ті, які не містять М.

Вектор, який підлягає включенню до базису, визначають за (m+2) рядком.

Ітераційний процес по (m+2) рядку проводять до повного виключення всіх штучних змінних з базису, потім процес визначення оптимального плану продовжують за (m+1) рядком.

Теорема 1. Якщо в оптимальному плані 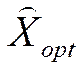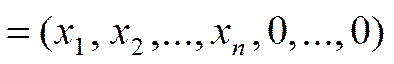розширеної задачі штучні змінні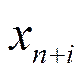 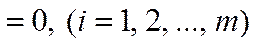, то план 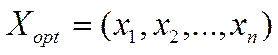є оптимальним планом початкової задачі.

Випадки.

1. Якщо в оцінковому рядку останньої симплексної таблиці оцінка 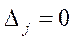відповідає вільній (небазисній) змінній, то це означає, що ЗЛП має альтернативний оптимальний план.

2. Якщо при переході у симплекс-методі від одного опорного плану задачі до іншого в напрямному стовпчику немає додатних елементів 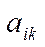, то це означає, що цільова функція задачі лінійного програмування є необмеженою й оптимальних планів не існує.

3. Якщо для опорного плану задачі лінійного програмування всі оцінки 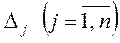задовольняють умову оптимальності, але при цьому хоча б одна штучна змінна є базисною і має додатне значення, то це означає, що система обмежень задачі несумісна й оптимальних планів такої задачі не існує.

Читайте також:

1. II. Критерій найбільших лінійних деформацій
2. АНАЛІЗ ЛІНІЙНИХ МОДЕЛЕЙ ЕКОНОМІЧНИХ ЗАДАЧ
3. Аналіз та синтез моделей систем
4. Аналіз трифазного з’єднання з урахуванням опорів лінійних проводів
5. Використання спеціальних моделей відведення земельних ділянок під будівництво (державно-приватне партнерство, індустріальні парки, реконструкція кварталів застарілої забудови).
6. Використання у мові словотворчих моделей для творення нових назв
7. Вимірювання лінійних переміщень, вібрацій та деформацій
8. Вимірювання лінійних та кутових розмірів
9. Вимірювання лінійних та кутових розмірів
10. Вимоги до математичних моделей
11. Відкритість національної економіки і конвертованість моделей національних економічних систем
12. Впровадження моделей сприйняття

Переглядів: 451