• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розгалужені електричні кола. Закони Кірхгофа. З’єднання провідників

Для розрахунку складних розгалужених електричних кіл зручно користуватись законами Кірхгофа, які є наслідками закону збереження електричного заряду і законів Ома.

Вузлом електричного кола називається місце з’єднання трьох або більше провідників. Розглянемо деякий вузол А (рис.3.31). В стаціонарному випадку заряд і потенціал точки А повинен залишатись постійним. Виходячи із закону збереження електричного заряду можна записати

, (3.191)

де – заряди, які за деякий однаковий проміжок часу надходять до вузла А чи виходять із нього. Продиференціюємо вираз (3.191)

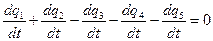. (3.182)

Враховуючи формулу (3.156) вираз (3.192) можна представити у вигляді

. (3.193)

Будемо вважати сили струмів, які сходяться у вузлі, алгебраїчними величинами. Зокрема, струми, які ідуть до вузла, будемо вважати додатними, а струми, які ідуть від вузла, будемо вважати від’ємними. Тоді в загальному випадку, коли у вузлі сходиться 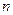провідників, формулу (3.193) можна представити у вигляді

. (3.194)

Формула (3.194) є математичним записом першого закону Кірхгофа: алгебраїчна сума сил струмів, які сходяться у вузлі, рівна нулю. При цьому струми, які йдуть до вузла вважаються додатніми, а струми, які йдуть від вузла – від’ємними.

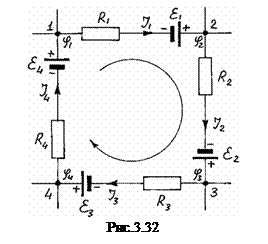Розглянемо довільний замкнутий контур, який умовно виділимо в складному розгалуженому електричному колі (рис. 3.32). Будемо вважати, що внутрішні опори джерел струму рівні нулю. На кожній ділянці контуру виберемо довільним чином напрямки струмів. Виберемо довільним чином напрямок обходу по контуру, який будемо вважати додатнім. Запишемо для кожної ділянки контуру закон Ома для неоднорідної ділянки кола

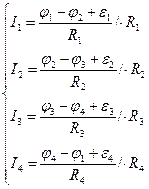(3.195)

Помножимо кожне з рівнянь системи (3.195) на опори відповідно

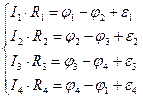(3.196)

Додамо алгебраїчно рівняння системи (3.196)

. (3.197)

Якщо виділений контур містить n ділянок, то формула (3.197) в загальному випадку може бути представлена у вигляді

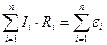. (3.198)

Це математичний запис другого закону Кірхгофа: при обході по замкнутому контурі алгебраїчна сума добутків сил струмів на опори рівна алгебраїчній сумі електрорушійних сил. При цьому струм вважається додатнім, якщо його напрямок співпадає з напрямком обходу за контуром; електрорушійна сила вважається додатною, якщо при обході здійснюється перехід через неї із знаку “мінус” на знак “плюс”.

Серед різних видів з’єднання провідників найпростішими і найважливішими є послідовне і паралельне з’єднання.

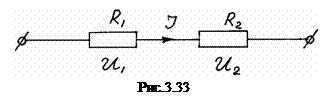Розглянемо послідовне з’єднання провідників. При цьому з’єднанні електричне коло не має розгалужень, усі провідники ввімкнені в коло по черзі, один за одним. На рис.3.33 показано з’єднання двох провідників з опорами і . При проходженні постійного струму електричний заряд не нагромаджується в жодному з провідників. За один і той же проміжок часу через поперечний переріз кожного з провідників проходить один і той же заряд, а значить сила струму в усіх провідниках однакова

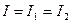. (3.199)

При проходженні заряду послідовно через усі провідники виконується робота, яка рівна сумі робіт виконаних на кожному провіднику. Тому загальна напруга рівна сумі напруг на всіх провідниках

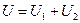. (3.200)

Поділимо вираз (3.200) на силу струму І. Врахувавши при цьому (3.199), одержимо

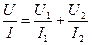. (3.201)

Із закону Ома для ділянок кола (3.162) випливає, що

. (3.202)

З врахуванням формули (3.202) вираз (3.201) набере вигляду

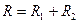. (3.203)

Формула (3.203) дозволяє визначити загальний опір при послідовному з’єднанні двох провідників. Якщо послідовно з’єднано n провідників, то формула (3.203) набере вигляду

. (3.204)

Розглянемо паралельне з’єднання двох провідників з опорами і (рис. 3.34). При такому з’єднанні початки всіх провідників з’єднуються в одному вузлі, а кінці провідників – в іншому вузлі. Оскільки потенціали початків провідників у вузлі А рівні 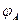, а потенціали кінців провідників у вузлі В рівні , то різниці потенціалів і напруги на всіх провідниках однакові

. (3.205)

У випадку постійного струму в будь-якій точці електричного кола, в тому числі і у вузлі А, заряди не накопичуються. Тому сила струму, який надходить до вузла А повинна дорівнювати сумі сил струмів, які виходять з цього вузла.

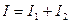. (3.206)

Поділимо вираз (3.206) на напругу і врахувавши (3.195), одержимо

. (3.207)

Із закону Ома для ділянки кола отримаємо

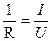. (3.208)

З врахуванням виразу (3.208) формула (3.207) набере вигляду

. (3.209)

Формула (3.209) дозволяє визначити загальний опір при паралельному з’єднанні двох провідників. Якщо паралельно з’єднано n провідників то формула (3.209) набере вигляду

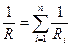. (3.210)

Читайте також:

1. IV. Закони ідеальних газів.
2. Австрійська школа.
3. Аграрні закони України
4. Американська школа.
5. Аналіз трифазного з’єднання з урахуванням опорів лінійних проводів
6. Анатомія кісток верхньої і нижньої кінцівок та їх з’єднання
7. Б- не збуджена ділянка мембрани , на яку діють електричні струми збудженої ділянки. Стрілками показано напрям струмів, кружечками – дійсне переміщення іонів.
8. Багатоконтурні лінійні електричні ланцюги
9. База управлінських рішень і закони організації.
10. Безперервні з’єднання – сінартрози
11. БІОЕЛЕКТРИЧНІ ПОТЕНЦІАЛИ
12. Біоелектричні явища в тканинах: будова мембран клітини, транспорт речовин через мембрану, потенціал дії та його розповсюдження.

Переглядів: 4128