• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Підкидання монети по телефону

3.1. Попереднє обговорення.Уявимо таку ситуацію. Національні футбольні збірні України та Бразилії вирішили провести одну товариську гру і їм належить домовитися, на чиєму полі вона відбудеться. Справедливо було б вирішити це питання жеребкуванням. Чи обов'язково з цією метою командам влаштовувати особисту зустріч своїх представників? Протокол підкидання монети дозволяє провести жеребкування на відстані за допомогою телефону (телеграфу, електронної пошти тощо).

Ідею протоколу можна зрозуміти на такому прикладі. Припустимо, що Аліна мешкає в Києві, а Боб у Ріо-де-Женейро. Нехай їм потрібно вирішити, хто до кого приїздить в гості. Вони домовляються спільними зусиллями згенерувати випадковий біт r, з однаковою ймовірністю рівний 1 або 0, з тим, що коли випаде r = 0, то Боб прилітає до Аліни, а коли r = 1, то Аліна вилітає в Ріо. Питання полягає в тому, як отримати r.

1-ий сценарій. Аліна підкидає монетку і результат — "чіт" (r = 0) чи "лишок" (r = 1) повідомляє Бобові телефоном. Таке вирішення проблеми дещо не влаштовує Боба — він не до кінця впевнений, що Аліна не схитрувала.

2-ий сценарій. І Аліна, і Боб підкидають кожен свою монетку. Нехай у Аліни випало а {0,1}, а у Боба b {0,1}. Вони покладають r = аb. Зрозуміло, що якщо а і b — випадкові біти, то r також. Більше того, навіть якщо хтось один з партнерів хитрує, але інший поводиться чесно, то r все одно набуває значення 0 та 1 рівноймовірно (довести!). Тому це добрий підхід до справи, але заковика, в тому, що щойно сказане стосується лише випадку, коли а і ь незалежні. В дійсності ж Аліна може спершу вислухати результат підкидання монети Бобом, а тоді у якості свого назвати той же біт, забезпечивши цим r = 0 і уникнувши довгих перельотів, яких вона недолюблює.

3-ій сценарій показує, як обійти цю проблему. Аліна підкидає монетку, записує біт а, і авіапоштою посилає його Бобові. Наступного дня, коли лист із штемпелем Київської головпошти вже в дорозі, але ще не дійшов за призначенням, Аліна та Боб зідзвонюються, Боб першим називає свій біт ь, після чого Аліна називає свій. Цього разу вона не може схитрувати, тому що згодом Боб отримає біт а поштою і зможе виявити підміну.

3.2. Протокол на основі ймовірнісного криптування.В наступ­ному протоколі реалізовано 3-ій сценарій, лише контрольне посилання біта а авіапоштою вирішується в режимі реального часу суто криптографічними засобами. Протокол використовує довільну надійну систему ймовірнісного криптування (див. § V.4). Через Е і D позначимо алгоритми шифрування і дешифрування цієї системи, а через К і К' -відкритий і таємний ключі. Нагадаємо, що Е_к(0) та E_к(1), результати шифрування однобітових повідомлень, є випадковими величинами, які неможливо ефективно розрізнити з імовірністю, суттєво більшою за 1/2. Буде використовуватись ще одна властивість, якою володіють всі конкретні криптосистеми з відкритим ключем: за заданою парою (К, К') можна ефективно перевірити, чи вона справді породжена алгоритмом генерування ключів системи.

Щоб отримати біт r, який вони обоє визнають за випадковий, Аліна і Боб чинять так.

• Аліна вибирає свій біт а і пару ключів (К,К'). Після цього зашифровує а і результат с = E_к(0) разом з ключем К посилає Бобові.

• Боб вибирає біт ь і посилає його Аліні.

• Аліна посилає Бобові дешифруючий ключ К'.

• Боб перевіряє, що (К,К') справді є парою шифруючого та дешифруючого ключів, і обчислює а = D_K'(с).

• Обоє обчислюють r = а b.

Як і у описаному вище 3-му сценарії, Аліна позбавлена можливості злукавити, бо посилає свій біт ще перед тим, як довідається Бобів. Боб теж не здатен хитрувати, бо отримує Алінин біт у зашифрованому вигляді і не може його відтворити без дешифруючого ключа К’, звичайно за умови, що використовується надійна криптосистема.

Подивимось, як виглядає конкретне втілення поданого вище прото­колу з використанням ймовірнісного криптування на основі розпізнавання квадратичності.

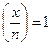• Аліна вибирає досить великі прості числа р та q і обчислює їх добуток п = pq, після чого вибирає біт a. Далі вона генерує число х J_n із символом Якобі так, що х є випадковим квадратичним лишком за модулем п, якщо а = 0, і випадковим псевдоквадратом, якщо а = 1.

• Аліна посилає Бобові х і п.

• Боб вибирає біт bі посилає його Аліні.

• Аліна відкриває Бобові прості р і q Боб пересвідчується, що справді pq = n. Далі він застосовує алгоритм із пункту IV.4.3 і з його допомогою визначає, чи х Q_n, тим самим отримуючи біт а. Аліна і Боб обоє обчислюють r = аb.

3.3. Протокол на основі дволистої'функції із секретом. Розглянемо ще один протокол підкидання монети. Він використовує дволисту важкооборотну функцію із секретом. Мається на увазі функція f з такими властивостями:

1) f обчислюється ефективно;

2) для кожного х існує єдине таке, що f(x) = f(x');

3) х' можна, ефективно обчислити за х, лише якщо знати секретний ключ К.

(У деталях важкооборотні функції розглядались в § VI. 1)

Прикладом дволистої важкооборотної функції з секретом є функція Рабіна піднесення до квадрату за модулем п, якщо звузити її область визначення до {1, 2,...,(п - 1)/2}. Нагадаємо, що n = pq є тут цілим числом Блюма, тобто добутком двох простих з властивістю .

Новий протокол підкидання монети влаштований так.

• Аліса вибирає функцію f і повідомляє про це Боба, втаївши секретний ключ К.

• Боб вибирає випадковий елемент х, обчислює у = f(x) і посилає у Алісі.

• Аліса за допомогою секретного ключа К обчислює обидва прообрази х₁ та x₂ елемента у: f(x₁) = f(x₂) = y Потім вибирає один із цих прообразів, скажімо x_i, і посилає його Бобові.

• Якщо 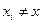, то Боб знає обидва прообрази {х_i,х} = {х₁, x₂}елемента у і посилає їх Алісі. Аліса і Боб покладають r = 0.

• Якщо x_і = х, то Боб визнає, що не знає другого прообразу. В цьому випадку Аліса і Боб покладають r = 0.

• Аліса посилає Бобові секретний ключ К, і Боб перевіряє, що у мав справді два прообрази.

ВПРАВИ

3.1. Аліна і Боб живуть в одному місті. Реалізувати 3-ій сценарій підкидання монети по телефону (пункт 3.1), виходячи з припущення, що обоє мають під рукою телефонну книгу.

3.2. Розробити протокол підкидання монети, який би використовував ймовірнісну криптосистему на основі

a) RSA функції (пункт V.4.3);

b) довільного предикату з секретом (пункт VI. 1.4).

3.3.Пояснити, чому протокол з пункту 3.3 є справедливим, тобто ні Aліса, ні Боб не здатні вплинути на розподіл біту r (за умови, що хоча б хтось один із них не хитрує, тобто притримується протоколу).

3.4. Нехай п є цілим Блюма. Довести, що звуження функції SQUARE(x) = х² mod n на область {1,2,..., (n-1)/2} справді володіє трьома властивостями дволистої важкооборотної функції з секретом, за умови важкості факторизації цілих Блюма.

3.5.а) Реалізувати протокол підкидання монети з пункту 3.3 на основі функції SQUARE з областю визначення {1, 2,..., (п - 1)/2}.

ь) Довести, що у випадку r = 1 Боб здатен самостійно визначити секретний ключ р, q.

ЛІТЕРАТУРА

Задача підкидання монети на відстані була поставлена і розв'язана в [76].

Читайте також:

1. Ділова розмова по телефону
2. Монети системи Стародавньої Греції
3. Монетизація бюджетного дефіциту і ВВП в Україні
4. Монетизація бюджетного дефіциту та валового внутрішнього продукту в Україні
5. Побудова, принцип роботи і основні параметри безпроводового телефону
6. Правила спілкування фахівця по телефону
7. Принцип дії телефону
8. Швидкість обігу грошей, коефіцієнт монетизації.

Переглядів: 1400