• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розподіл таємниці

Гра в карти заочно

Аліса і Боб, знаходячись на відстані одне від одного, вирішили розважитись грою в покер. Хоча зв'язок між ними добре налагоджений, скажімо, за допомогою Інтернету, залишається проблема чесної роздачі карт. Однак і ця проблема вирішується за допомогою протоколу заочної гри в карти.

Описаний нижче протокол використовує довільну комутативну криптосистему. Алгоритми шифрування і дешифрування Аліси позначимо через Е_а і D_a, а Боба — через E_B і D_B • Комутативність кри-птосистеми означає, що для будь-якого повідомлення М справедлива рівність

Е_В(Е_А(М)) = Е_А(Е_В(М)).

Прикладом такої системи Є модифікація RSA, де модуль п учасники вибирають спільно, а шифруючі/дешифруючі експоненти е і d -таємно одне від другого. Для іншого варіанту комутативної криптосистеми модуль п вибирається простим. В обидвох випадках учасник X вибирає пару із шифруючого ключа е_Х і дешифруючого d_Х з властивістю 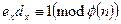, і здійснює шифрування/дешифрування за формулами

Е_Х(М) = М^ех mod n, D_X(M) = M^dx mod n

Перейдемо до опису протоколу.

• Аліса і Боб досягають згоди про кодування карт словами М₁,...,М₅₂, і домовляються, яка саме комутативна криптосистема буде використовуватись.

• Обидвоє таємно одне від другого вибирають собі шифруючий та дешифруючий ключі.

• Аліса зашифровує повідомлення М₁,...,M₅₂, перемішує випадковим чином криптотексти Е_А(М₁),...,Е_А(М₅₂) і посилає їх Бобові.

• Боб вибирає випадкові п'ять криптотекстів, і посилає їх назад Алісі. Це карти, якими буде грати Аліса.

Коментар. Боб не може визначити карт Аліси, бо не знае її ключа.

• Із карт, що залишилися, Боб вибирає ще п'ять Е_А(М_і1),...,Е_А(М_і5) для себе.

Коментар. Боб вибрав карти у зашифрованому вигляді і тепер повинен довідатись, які це власне карти. Це він може зробити лише за допомогою Аліси, але повинен подбати, щоб при цьому його карти не відкрилися і їй.

• Боб зашифровує відібрані Е_А(М_і1),...,Е_А(М_і5) за допомогою власного ключа і криптотексти Е_в(Е_А(М_і1)) = Е_А(Е_в(М_і1)),...,Е_в(Е_А(М_і5)) = Е_А(Е_В(М_і5]} посилає Алісі.

• Аліса дешифрує отримані криптотексти і повертає Бобові результат Е_B(M_і1),...,E_В(M_і5).

Коментар. Аліса, яка не знає ключів Боба, не може звідси визначити його карти.

• Боб дешифрує надіслані Алісою E_В(M_і1,...,Е_В(М_і5) і отримує свою п'ятірку карт M_і1,...,М_і5.

• В кінці гри Аліса, і Боб обмінюються ключами і перевіряють, що ніхто з них не хитрував.

ВПРАВИ

4.1.Припустимо, що при роздачі карт Аліса і Боб використовують комутативну криптосистему, яка є котроюсь із двох згаданих модифікацій системи RSA. Аліса довіряє Бобові вибрати коди карт М₁,..., М₅₂ в Z_n. Перші чотири карти є тузами, і Боб "позначає" їх, вибравши коди так, що 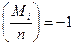для і ≤ 4 і для і > 4. Яким чином під час подальшого виконання протоколу роздачі карт Боб зможе розпізнавати тузи?

ЛІТЕРАТУРА

Протокол заочної гри в покер запропоновано в [59]. Криптоаналіз проведено в [115, 84].

Аліса і Боб тримають у сейфі цінні папери, які є їхнім спільним надбанням. Сейф замикається на два замки. Один ключ зберігається в Аліси, а інший у Боба. Завдяки цьому Аліса і Боб можуть розпоряджатися цінностями лише за обопільною згодою.

Якщо цінності є у спільному володінні Аліси, Боба та Вітольда, і будь-яке рішення приймається більшістю голосів, то потрібен сейф складнішої конструкції. Замок повинен мати три отвори для трьох різних ключів, причому він повинен відкриватися будь-якою парою ключів, і не повинен відкриватися лише одним ключем.

Подібна ідея розподілу ключа між кількома особами покладена в основу протоколу розподілу секрету. Нехай натуральне число s є цінною секретною інформацією (номер рахунку у швейцарському банку, код команди на запуск балістичної ракети тощо). Завданням протоколу є так подрібнити секрет s на частини, по одній для кожного із п учасників, щоб будь-які k учасників могли відновити s, поєднавши свої частинки, але щоб ніяка група з k - 1 учасника цього зробити не могла. Формально йдеться про процедуру, яка б співставляла числу s послідовність чисел s₁.,..., s_n і при цьому виконувались такі дві умови:

1) s можна ефективно отримати з довільної k-елементної підпослідовності s_s1,...,s_ik;

2) s в принципі не можна отримати ні з якої (k - 1) елементної послідовності.

Ми опишемо протокол, запропонований Аді Шаміром в [140].

Вибирають досить велике просте число р і розглядають s як елемент поля Z_Р. Покладають a₀ = s, і вибирають в Z_p випадковим чином числа a₁,...,a_k-1. Нехай f(x) - многочлен від змінної х з коефіцієнтами в Z_p. і-ий учасник протоколу, де 1 ≤ I ≤ п, отримує значення s_i = f(i).

Читайте також:

1. I. Доповнення до параграфу про точкову оцінку параметрів розподілу
2. IV. Розподіл нервової системи
3. V. Розподільний диктант.
4. Авоматизація водорозподілу регулювання за нижнім б'єфом з обмеженням рівнів верхнього б'єфі
5. Автоматизація водорозподілу з комбінованим регулюванням
6. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
7. Автоматизація водорозподілу регулювання зі сталими перепадами
8. Автоматизація водорозподілу регулюванням з перетікаючими об’ємами
9. Автоматизація водорозподілу регулюванням за верхнім б'єфом
10. Автоматизація водорозподілу регулюванням за нижнім б'єфом
11. Алгоритм розв’язання розподільної задачі
12. Аналіз ефективності використання каналів розподілу

Переглядів: 769