Доведення без розголошення

6.1. Доведення квадратичності.В якості першого прикладу ми розглянемо доведення факту, що деяке число є квадратичним лишком за модулем п. Як зазначалось в § IV.4, задача розпізнавання квадратичних лишків є важкою, якщо тільки не є відомим розклад модуля n на прості множники. Тому Аліса за парою (х,п) неспроможна (за поліноміальний від log n час) визначити, чи справді ж є квадратичним лишком.

Припустимо, що на відміну від Аліси, Боб знає якийсь квадратний корінь з х за модулем п. Позначимо цей корінь через у: . Нас не цікавить яким саме чином Боб добув корінь з х. Найправдоподібнішим поясненням таких виняткових обчислювальних здібностей може бути те, що Боб або власноручно вибрав n і знає його розклад на множники, або спершу вибрав у, а вже потім обчислив х = у² mod n.

Найпростіший спосіб, у який Боб може переконати Алісу. що х Q_n, це просто показати їй у. А наступний протокол дозволяє переконати Алісу не лише без пред'явлення їй коренів, але й без надання їй жодної інформації, яку Аліса не змогла б здобути самотужки.

Вхід: (х, п), де ж і існує у таке, що .

• Боб вибирає випадковий елемент v в , підносить його до квадрату і результат u= v² mod n посилає Алісі.

• Аліса посилає Бобові випадковий біт b{0,1}.

• Боб посилає Алісі число

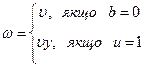
Якщо b = 0, то Аліса перевіряє, чи справді , а якщо ь = 1, то перевіряє, чи справді 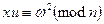. Якщо результат перевірки негативний, то Аліса припиняє діалог і звинувачує Боба в ошуканстві.

Все вищеописане повторюється m = [logn]разів, щоразу із незалежним вибором випадкових величин. Якщо результат перевірки у кожному циклі був успішним, то Бобові вдається переконати Алісу, що х Qn-Перелічимо три основні властивості цього протоколу.

1) Повнота. Якщо справді хQ_n, а Боб справді знає квадратний корінь у і діє згідно з протоколом, то він переконує Алісу з імовірністю 1. Цю властивість легко перевірити, безпосередньо прослідкувавши за перебігом протоколу.

2) Обгрунтованість. Якщо ж х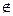 Q_n, то як би винахідливо Боб не діяв, тобто які б хитрі повідомлення u і w не посилав Алісі, вона викриє його нещирість з імовірністю 1/2 в кожному із циклів, і з ймовірністю 1 – 2^-^m хоча б в одному з т циклів. Таким чином, Боб може переконати Алісу у справедливості хибноготвердження з імовірністю щонайбільше 1/п, що єекспоненційно малою величиною в порівнянні з довжиною входу.

Щоб довести цю властивість, розглянемо два випадки.

Випадок 1: Перше повідомлення Боба Алісі u не є квадратичним лишком за модулем п. Тоді Боба буде викрито при ь = 0, що трапиться з імовірністю 1/2.

Випадок 2: Повідомлення u є квадратичним лишком за модулем п. Тоді хu не є квадратичним лишком і Боба буде викрито при ь = 1, що теж трапиться з імовірністю 1/2.

3) Відсутність розголошення. Якщо справді х Q_n, то Аліса не отримує від Боба ніякої інформації. Це твердження досить переконливе інтуїтивно. Справді, якщо Аліса вибирає біт ь = 0, то отримує випадковий квадратичний лишок u і корінь з нього w. Якщо ж ь = 1, то Алісі дістається квадратний корінь w з хu, причому хu також є випадковим квадратичним лишком за модулем п (див. пункт а вправи ПІ.3.8).

Для того, щоб формалізувати це спостереження, позначимо через VIEW_x_,_n всю інформацію, яку сприймає Аліса упродовж одного циклу протоколу на вході (х,п), а саме, VIEW_x_,_n = <u,ь,w>. Аліса спостерігає кожну конкретну трійку <u, ь, w> з певною ймовірністю, тобто VIEW_x,n є випадковою величиною.

Для довільного ймовірнісного алгоритму М результат його роботи на вході (х, п) позначимо через М(х, п). Слід звернути увагу на те, що М(х, п) є випадковою величиною, значення якої залежить від випадкової послідовності алгоритму.

Абсолютно строго властивість відсутності розголошення можна сформулювати так: існує поліноміальний ймовірнісний алгоритм М такий, що при х Q_n випадкові величини М(х, п) і VIEW_x_,n однаково розподілені. Таким чином, VIEW_x_,_n нe містить для Аліси ніякої нової інформації в тому сенсі, що Аліса могла б отримати все абсолютно те ж саме, запустивши алгоритм М на вході (х, п).

Нам залишається описати алгоритм М, який симулює діалог Аліси і Боба на входах (х, п) при х Q_n Спочатку слід вибрати випадковий елемент w і випадковий біт b (0,1). Якщо b = 0, то покласти u = w²mod n. Якщо ь = 1, то покласти u = w²x^-¹mod n. Трійку <u, b, w>. подати на вихід.

Насправді наведений протокол володіє властивістю відсутності розголошення у значно сильнішій формі. Зауважимо, що випадкова величина VIEW_x_,_n залежить від дій Аліси. Ми виходили з того, що Аліса притримується протоколу. Але ж вона може хитрувати в надії вивідати у Боба чим більше інформації. Наприклад, Аліса може посилати Бобові біт ь, вибраний не рівноймовірно, а за якимось іншим розподілом. З врахуванням цієї можливості, властивість відсутності розголошення розглянутого протоколу можна сформулювати у підсиленому варіанті, Нехай Аліса вибирає своє повідомлення ь як результат роботи деякого поліноміального ймовірнісного алгоритму А на вході <х,п,u> (це вся інформація, доступна Алісі на момент вибору). Тоді існує поліноміальний ймовірнісний алгоритм М_A такий, що при х Qn випадкові величини M_A(х,п} і VIEW_x,n однаково розподілені.

Протокол з такою властивістю відсутності розголошення називають досконалим доведенням без розголошення.

6.2. Доведення неквадратинності.Тепер розглянемо доведення без розголошення того факту, що х не єквадратичним лишком за модулем п. Зразу обмежимось випадком, коли 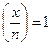, тобто х J_n, бо інакше доведення давалося б простим обчисленням символу Якобі (див. пункт 5 твердження IV.1.7). Отже Боб, який вміє розпізнавати квадратичність за модулем п (наприклад, знаючи розклад п на прості множники), хоче переконати Алісу, що х не є квадратичним лишком, тобто належить множині псевдоквадратів Q_n.

Вхід: (х,п), де х Q_n.

• Аліса вибирає випадковий елемент v в і випадковий біт b {0,1}.

Далі Аліса обчислює

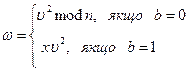і посилає w Бобові.

• Боб визначає, чи w є квадратичним лишком за модулем п і посилає Алісі у відповідь біт

• Аліса перевіряє, чи b = b'. Якщо це не так, Аліса припиняє спілкування з Бобом і оголошує йому недовіру.

Все повторюється m = [logn] разів, щоразу із незалежним вибором випадкових величин. Якщо результат перевірки у кожному циклі був успішним, то Бобові вдається переконати Алісу, що х 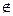Q_n.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Розподіл таємниці	\|	Ідентифікація

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.004 сек.