• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Цифровий підпис

Розглянимо таку ситуацію. Брокер від Київського акціонерного банку „Геркулес” вигідно прибав на Токійській фондовій біржі портфель цінних паперів, висталених Нью-Йоркським Сіті банком. Оплата має бути переведена з Києва на Волл Стріт протягом години. Подібні фінансові операції проводяться через електронні засоби зв’язку. Це робить неможливим використання традиційних засобів засвідчення платіжних документів на зразок великої гербової печатки та підпису головного бухгалтера. Але як тоді банкові вберегтися від злодія-інтелектуала, який добре знається і на фінансах, і на електроніці, і може від імені брокера послати вимогу перевести гроші на власний підставний рахунок. Це завдання вирішується за допомогою протоколу цифрового підпису. Ми почнемо з конкретної реалізації такого протоколу на базі системи RSA.

2.1. Підпис у системі RSA.Нагадаємо, що в системі RSA кожен абонент Х має пару ключів – загальновідомий відкритий (п_х,е_х) і таємний d_x, який знає лише Х і ніхто інший. Таким чином, будь-хто може скористатися алгоритмом шифрування Е_х абонента Х, але тільки він сам володіє алгоритмом дешифрування d_x. Важливим є виконання таких співвідношень для довільного повідомлення М:

D_x(E_x(M)) = E_x(D_x(M)) = M. (1)

Ці співвідношення зводяться до рівностей (M^ex)^dx = (M^dx)^ex = М в Z_nx, і виражають той факт, що шифруюче відображення е_х та дешифруюче d_x є взаємно оберненими.

Припустимо тепер, що Аліса хоче послати Бобові повідомлення М таким чином, щоб той був певен, що повідомлення справді послане Алісою, а не її суперницею Агнесою. Для цього пропонується такий протокол, в якому (Е_a,, D_A) та (Е_Ь, D_Ь) — алгоритми шифрування та дешифрування Аліси та Боба.

• Аліса обчислює С = E_Ь (D_a(m)) і посилає С Бобові.

• Боб, отримавши С, обчислює М = E_a(D_ь(C}).]

Коректність протоколу зводиться до рівності

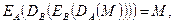
яка випливає із співвідношень (1).

Ефективність. Аліса та Боб використовують ефективні алгоритми шифрування та дешифрування криптосистеми RSA. Зауважимо, що Аліса використовує свій приватний алгоритм d_a та відомий всім алгоритм E_Ь- Те ж саме із Бобом — він використовує особистий алгоритм d_b і загальновідомий алгоритм е_а

Конфіденційність. Під конфіденційністю цього протоколу ми розуміємо його надійність як звичайної криптосистеми для пересилання по­відомлень. В такому розумінні конфіденційність є досить інтуїтивним фактом, що грунтується на надійності системи RSA. Перед суперницею Аліси Агнешкою, яка підслухала криптотекст С, виникає завдання визначити М із E_b(D_A(M)). Припустимо, що Агнешка знає навіть набагато більше, ніж їй слід, а саме Алісин приватний алгоритм D_a-Тоді визначення М для суперниці рівносильне визначенню D_A(М). Але визначення d_a(m) із e_b(d_a(m)) є нічим іншим, як задачею зламу RSA^1[3].

Достовірність. Під достовірністю ми розуміємо таку властивість протоколу підпису: Боб, і не тільки він, а будь-хто інший, може впевнитися, що відправником повідомлення є саме Аліса. Що стосується описаного вище протоколу, то Боб, який успішно розшифрував криптотекст С і прочитав повідомлення М, дійсно має вагомі підстави вважати, що воно послане саме Алісою. Справді, криптотекст має структуру С = E_b(D_A(M)), тоді інтуїтивно переконливим є висновок, що особа, яка послала С, мала би знати алгоритм D_A.²[4] Але алгоритм D_A відомий лише Алісі (якщо тільки Агнесі не вдалося зламати систему RSA).

2.2. Загальна схема.Описана в попередньому пункті криптосистема забезпечує як достовірність повідомлення, так і його конфіденційність. Є системи власне цифрового підпису, метою яких є забезпечення лише достовірності. Такі системи вкладаються у схему, що включає в себе наступні складові:

· Ймовірнісний алгоритм генерування ключів. Кожен абонент А отримує пару (К_А, К_А), де К_А – відкритий, а К’_А –таємний ключі.

· Алгоритм підписування SIGN, який отримавши на вхід довільне повідомлення М та таємний ключ К’_А, продукує слово S = SIGN(M, K’_A) в деякому алфавіті, яке називається підписом абонента А на повідомленні М. Коли А хоче послати комусь повідомлення М із запевненням, що воно відправлене саме ним, то посилає пару (M, S).

· Алгоритм підтвердження підпису CHECK, який є до послуг будь-кого, хто бажає перевірити, що підпис S повідомлення М належить саме власникові відкритого ключа К_А. Перевірка вважається успішною, якщо CHECK (К_А, М, S) = 1. Для будь-якого повідомлення М і для кожної пари ключів (К, К’) має виконуватись співвідношення

CHECK (K, M, SIGN(M, K’)) = 1.

Виконання цієї умови означає коректність системи цифрового підпису.

Всі алгоритми – генерування ключів, підписування та перевірки підпису- повинні бути ефективними.

Надійність такої системи підпису означає, що лише законний власник таємного ключа К’ може для повідомлення М виробити такий підпис S, який пройшов би перевірку, тобто для відповідного відкритого ключа К виконувалась рівність CHECK(K, M, S) = 1. Якщо ж такий підпис S знаходить суперник, то кажуть, що він підроблює або фальшує підпис легального абонента на повідомленні М.

Загроза підроблення підпису суперником може бути різних ступенів:

• екзистенційне фальшування — існує повідомлення М, підпис якого суперник може підробити (хоча це повідомлення може для нього не мати жодного інтересу);

• вибіркове фальшування — суперник здатен підробити підпис деяких повідомлень за власним вибором;

• універсальне фальшування — суперник може підробити підпис будь-якого повідомлення, хоча й не знає таємного ключа;

• повний злам системи підпису — суперник спроможний визначити таємний ключ.

При фальшуванні підпису суперник виходить із наявної у нього інформації. Залежно від того, якою саме інформацією він володіє, розрізняють різні види атак суперника (нагадаємо, що алгоритми генерування ключів, підписування та перевірки вважаються відомими суперникові завжди):

• атака за ключем — суперник знає лише відкритий ключ к_а абонента А;

• атака за відомим підписом — суперник знає пару (М, S), де повідомлення М було вибране абонентом А і S= SIGN(M, K'_A);

• атака з вибором повідомлень — суперник має можливість вибрати на власний розсуд певну кількість повідомлень m_i ,..., M_k і для кожного М_і отримати підпис S_i = SIGN (M_i ,K'}. (Наприклад, абонент А працює нотаріусом і зобов'язаний засвідчувати власним підписом електронні копії показаних йому паперових документів.).

Описана у попередньому пункті система цифрового підпису на базі RSA є частковим випадком загальної схеми, запропонованої Діффі та Гелманом в [20]. За цією схемою кожну криптосистему з відкритим ключем можна перетворити в систему цифрового підпису наступним чином; Нехай Е і D — алгоритми шифрування і дешифрування, К і К' — відкритий і таємний ключі, а М — довільне повідомлення. Тоді SIGN(M,K'} = D_K’(M) і

CHECK(K, M, S) =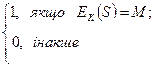

2 3 Система цифрового підпису ЕльГамала.Як ікриптосистеми для забезпечення конфіденційності повідомлень, системи цифрового підпису допускають ймовірнісну модифікацію. У ймовірнісних системах підпису алгоритм SIGN є не детермінованим, а ймовірнісним. Він продукує підпис S, що є випадковою величиною. У цьому і наступних пунктах 2.5 та 2.6 описуються деякі популярні серед практиків ймовірнісні системи цифрового підпису.

Першою ми розглянимо систему ЕльГамала [88]. Вона ґрунтується на тій же ідеї, що й криптосистема із § V.5.

Генерування ключів. Вибирають велике просте р, а також число g, 1 < g < p - 1, яке має в мультиплікативній групі великий порядок. В ідеальному випадку g є первісним коренем за модулем р. Числа g і p не є таємницею і перебувають в загальному користуванні. Кожен абонент вбирає собі випадкове число а у проміжку від 1 до p-1, і обчислює h = g^amod p.

Відкритий ключ: p, g, h.

Таємний ключ: a.

Підлисування. Аліса виробляє свій підпис S на повідомленні М таким чином. Вона

· вибирає випадкове число r ;

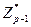· обчислює s₁ = g^rmod p;

· обчислює r’ = r^-1mod (p-1);

· обчислює s₂ = (M-as_-1)r’ mod (p-1);

· покладає S = (s₁, s₂).

Підтвердження підпису.

· Боб перевіряє, чи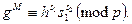

Коректність. З правил обчислення r’ і s₂ випливає, що 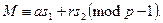Звідси з використанням теореми Ойлера отримуємо

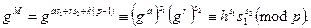
2.4. Коди достовірності.В цьому пункті ми ознайомимось із корисним засобом, який доцільно використовувати в будь-якій системі цифрового підпису.

Нехай функція f відображає повідомлення М довільної довжини у слово фіксованої довжини, скажімо 128-бітове. Припустимо, що f обчислюється ефективно. Тоді така функція називається вкорочуючою.

Пара різних повідомлень М₁ та М₂, для яких виконується рівність f(N₁)=f(N₂), називається клешнею або колізією функції f(див. малюнок 1).Якщо для f неможливо за реалістичний час знайти колізію, то така функція вкорочення називається безколiзійною.

Малюнок 1. Колізія вкорочуючої функції /.

Слід підкреслити, що оскільки розглядається функція f, яка є скіненним об'єктом, то слова "ефективно" і "за реалістичний час" вжиті вище не у формальному, а в інтуїтивному і суто практичному значенні. Відзначимо важливу властивість безколізійної функції f — для більшості аргументів М досить великої довжини, за заданим образом f(М) неможливо ефективно знайти таке М', що f(М') = f(М) (див. вправу 2.3). Це не що інше, як властивість важкооборотності, що була предметом вивчення у § VI. 1.

Образ f(М) називають вкороченням повідомлення М. У системах цифрового підпису вигідно підписувати не саме повідомлення М, а його вкорочення f(М) здійснене за допомогою обумовленої безколізійної вкорочуючої функції f, тобто варто покласти S = SIGN(f(M),K'). Виграш від цього очевидний: оскільки f(М) має фіксовану довжину для як завгодно довгих повідомлень, то фіксованою буде й довжина підпису S. Достовірність такого підпису не знижується. Теоретично, у суперника з'являється зайвий шанс для фальшування — підглянутий підпис S повідомлення М він міг би використати як підпис іншого повідомлення М' такого, що f(M') = f(M). Але це було б рівнозначним знаходженню суперником колізії для функції f, що вкрай малоймовірно з огляду на її безколізійність.

Варіант вкорочуючої функції з ключем називають кодом достовірності. Якщо f - вкорочуюча функція з ключем, то код достовірності повідомлення М рівний f(M, K). Той факт, що f(M, K) отримано справді з М може перевірити лише особа, яка знає ключ К. Код достовірності є криптографічним аналогом контрольної суми. І контрольну суму, і код достовірності долучають до повідомлення при його пересиланні, першу — щоб перевірити, чи повідомлення не було пошкоджене внаслідок природних перешкод у каналі зв'язку, а другий -щоб перевірити, чи повідомлення на шляху до адресата не було по вністю чи частково підмінене. Кожну вкорочуючу функцію f можна перетворити у функцію з ключем f', поклавши f'(M, К) = f(MK).

Прикладом вкорочуючої функції може бути така функція f, яка конструюється на основі функції RSA. Якщо /М / < Log₂ п, то f(M) = RSA(M). Для довших повідомлень М = М₁...М_l-1 М_l, розбитих на блоки відповідної довжини, функція задається рівністю f(M) = RSA(f(M₁...M_l-1)M₁).

На практиці використовуються швидші вкорочуючі функції, які вважаються безколізійними. Із найбільш популярних згадаємо MD5 та SHA. Перша спроектована Роном Райвестом, а друга — фахівцями з NIST та NSA (див. [137]). Всі такі функції вкорочують вхідний текст до 128 або й більше бітів. Зазначимо, що суттєво меншого вкорочення досягти неможливо, оскільки для довільної функції з множиною значень скажімо {0, 1}⁶⁴, цілком реально знайти колізію методом дня народження (див. вправу 2.5).

2.5. Система Шнорра.В цьому пункті ми опишемо ймовірнісну систему цифрового підпису, запропоновану Клаусом Шнорром у [138].

Генерування ключів. Вибирають велике просте число р таке, що р — 1 має досить великий простий дільник q (рекомендованими величинами є р > 2⁵¹² і q > 2¹⁴⁰). Вибирають також число 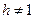таке, що 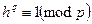. Параметри р, q, h не становлять таємниці і є спільними для всіх абонентів мережі.

Аліса вибирає випадкове число а в діапазоні від 1 до q — 1 і обчислює число v = (h^a)^-l mod p. її ключі формуються так.:

Відкритий ключ: v таке, що .

Таємний ключ: а.

Підписування. Алгоритм підписування використовує деяку вкорочуючу функцію f. Щоб виробити свій підпис S для повідомлення М, Аліса

• вибирає випадкове число r в діапазоні від 0 до q — 1;

• обчислює X = h^r mod p;

• обчислює s₁ = f(MX), де МX позначає результат злиття М і X в один текст;

• обчислює s₂ = (r + as₁) mod q;

• утворює S = (s₁,s₁).

Підтвердження підпису. Отримавши повідомлення М із підписом S=(s_I,s₂),Боб

• обчислює ;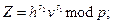

• перевіряє, чи s₁ = f(MZ).

Коректність. Якщо компонента підпису s₂ утворена, як передбачено протоколом, то Z = X. Справді,

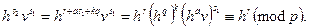
Тому, якщо й S₁ отримано згідно з протоколом, то перевірка відбувається успішно.

2.6. DSA. У 1991 році NIST запропонував у якості стандарту цифрового підпису систему DSA (від Digital Signature Algorithm). Цей стандарт носить назву DSS (від Digital Signature Standard) і опублікований в [122].

Генерування ключів. Вибирають велике просте число р таке, що р - 1 має досить великий простий дільник q. Стандарт вимагає, щоб 2⁵¹² < р < 2¹⁰²⁴ і q > 2¹⁶⁰. Далі вибирають у групі довільний елемент h порядку q (див. вправу 2.6). Параметри р, q, h не становлять таємниці і є спільними для всіх абонентів мережі.

Аліса вибирає випадкове число а в діапазоні від 0 до q - 1 і обчислює число ь = h^a mod p. її ключі формуються так.

Відкритий ключ: ь таке, що ь = h^a mod p.

Таємний ключ: а.

Підписування. Алгоритм підписування використовує вкорочуючу функцію f, в якості якої DSS пропонує функцію SHA [123] з довжиною вкорочення 160 бітів. Щоб виробити свій підпис S для повідомлення М, Аліса

• вибирає випадкове число r в діапазоні від 0 до q - 1;

• обчислює r’ = r^-l mod q;

• обчислює s₁ = (h^r mod p) mod q;

• обчислює s₂ = (r'(f(M) + as₁)) mod q;

• формує підпис S = (s₁,s₂).

Підтвердження підпису. Отримавши повідомлення М із підписом S= (s₁, s₂), Боб

• обчислює ;

• обчислює и₁ = (f(M)s') mod q;

• обчислює u₂ = (s₁s’) mod q;

• обчислює ;

• перевіряє рівність t = s₁.

Коректність. Припустимо, що підпис S = (s₁, s₂) отримано згідно з алгоритмом підписування. Досить перевірити, що 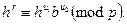.Оскільки ь = h^a mod p, то остання конгруенція рівносильна такій: 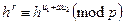Оскільки h має порядок q в , то необхідно і доситьперевірити, що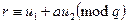або, еквівалентно, 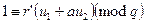. Підставивши у праву частину вирази для u₁ та u₂, отримаємо

,

що завершує перевірку коректності.

ВПРАВИ

2.1. Бобова секретарка Агнеса носить (посилає через локальну мережу) документи йому на підпис. Підписування здійснюється в системі RSA: подавши Бобові М, Агнеса отримує D_Ь(M). Документи бувають двох типів:

текстові, які Боб з цікавості перечитує перед тим як підписати, і цифрові — технічні чи фінансові звіти, які складаються з самих чисел, іякі Боб підписує відразу, лінуючись вникати в суть. Пояснити, як Агнеса може отримати підпис Боба на текстовому документі, що його Боб не підписав би ні за яких обставин.

2.2. ([130]) Аліса тримає в таємниці два великі прості числа р та q, і опри­люднює їх добуток п. Вякості підпису повідомлення М їй служить якийсь із квадратних коренів із М за модулем п (тут не йдеться про конфіденційність, а лише про достовірність). Розробити атаку з вибором повідомлення, яка б приводила до повного зламу цієї системи підпису.

2.3. Обгрунтувати, що безколізійна вкорочуюча функція є важкооборотною. Розглянути таку конкретну ситуацію. Нехай f: {0,1}*--> {0, 1}¹²⁸ не є важкооборотною з тої причини, що деякий ймовірнісний алгоритм А на вході f(x) длявипадкового х {0, 1}¹³⁰ швидко знаходить деяке х’, причому f(x') = f(x) з ймовірністю 1/2 (не виключено, що х' = х). Довести, що для випадкового х {0, 1}¹³⁰ пара х і х' = A(f(x)) утворює колізію функції f з імовірністю принаймні 1/8.

2.4. (Парадокс із днем народження)

а) Яке математичне сподівання кількості тих людей серед вибраних випадково п чоловік, чий день народження випадає того ж дня, що й у Вас^3[5]? Розглянути випадки п = 28, 365.

ь) Яке математичне сподівання кількості пар людей з однаковим днем народження серед вибраних випадковим чином п чоловік? Розглянути випадок п = 28.

c)Нехай із сукупності з п різних предметів вибираються з поверненням 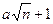предмет. Довести, що поміж вибраних предметів з імовірністю щонайменше 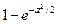знайдуться хоча б два однакові.

d)Оцінити знизу ймовірність того, що серед 28 чоловік знайдуться двоє з однаковим днем народження.

2.5. (Метод дня народження)

а) Припустимо, що функція f: {0,1}* —> {0, 1}⁶⁴ володіє такою властивістю однорідності. Для будь-якого фіксованого у {0, 1}⁶⁴ ймовірність того, що f(x) = у для випадкового елемента х {0, l}^k, де k ≥ 64, дорівнює 2^-64. Яке математичне сподівання кількості пар х і х' з однаковим образом f(x) = f(x') серед 2³³ елементів, випадково вибраних з {0,l}^k? Запропонувати ймовірнісну процедуру знаходження колізії для функції f.

Зауваження. Обчислення функції f від 2³³ аргументів не є непосильним завданням для сучасної обчислювальної техніки за умови, що однократне обчислення f займає мало часу.

ь) Нехай функція f така як у попередньому пункті, t — деякий фіксований текст довжини k ≥ 64 і х — випадковий текст такої ж довжини. Нехай Т = { th : h {0, 1}³² } і X = { xh : h {0, 1}³² }. Чому дорівнює математичне сподівання кількості пар t’ і х’ таких, що t' Т, х’ X і f(t') = f(x')?

c) ([151]) Нотаріус використовує систему цифрового підпису із вкорочуючою функцією f: {0,1}* —> {0, 1}⁶⁴. Пояснити, як зловмисник може з вагомою ймовірністю успіху отримати підпис нотаріуса на фальшивому документі t, давши нотаріусу на підпис "випадковий" безневинний документ х.

2.6. Нехай р та q — прості числа, і q| р - 1.

a) Припустимо, що g — первісний корінь за модулем р. Довести, що елемент h = g^(p-1)q mod р має порядок q в групі .

b) Нехай g — випадковий елемент групи , і h задається як у попередньому пункті. Довести, що з імовірністю 1 - 1/q порядок елемента h в , дорівнює q.

ЛІТЕРАТУРА

Класифікація атак проти цифрового підпису і мір їх успіху запозичена з [131]. Системам цифрового підпису на базі важкооборотних функцій при­свячена серія досліджень [100, 79, 120, 133]. В останній із цих робіт показано, що довільної важкооборотної функції досить, щоб сконструювати систему екзистенційно непідроблюваного підпису, стійку проти атаки з вибором повідомлень. Іншу техніку цифрового підпису запропоновано в [90]

ЛЕКЦІЯ 20

Читайте також:

1. Акт експертизи підписується кожним експертом і засвідчується печаткою медичної установи, на базі якої проводилася судово-психіатрична експертиза.
2. Аналоговий сигнал Цифровий сигнал
3. Болонський процес в Україні офіційно розпочався 19травня 2005 р.із підписанням декларації на Бергенській конференції.
4. Викладені письмово і підписані експертом роз'яснення і доповнення висновку приєднуються до справи.
5. Генерація ключа сеансу та попереднього підпису
6. Додаток В - Зразки підписів
7. Зіставлення підпису
8. Зіставлення підпису
9. Значним проривом у відносинах між Білоруссю, Казахстаном, Російською Федерацією і Україною стало підписання у 2004 р. Єдиного економічного простору (ЄЕП).
10. ІV. Підписання акта (довідки) документальної перевірки, порядок його (її) реєстрації та зберігання
11. Обчислення цифрового підпису
12. Обчислення цифрового підпису

Переглядів: 907