• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Типи бінарних відношень у теорії прийняття рішень

Розглянуті вище властивості бінарних відношень дають змогу означити типи бінарних відношень, важливі для ТРП: толерантності, еквівалентності, квазіпорядку (або півпорядку, неповного порядку) та строгого порядку (або лінійного порядку) [24].

ОЗНАЧЕННЯ 2.30. Толерантністю (байдужістю) називається відношення Р, яке водночас рефлексивне та симетричне.

Відношення толерантності будемо надалі позначати як І.

Приклад відношення толерантності – відношення нерозрізняльності, що виникає в разі вимірювання характеристик об’єктів: два об’єкти нерозрізненні за деякою ознакою, якщо різниця її значень не перевищує похибки вимірювання. Відношення толерантності нетранзитивне (нагромадження похибки при послідовних порівняннях об’єктів не дає підстав для висновку про нерозрізненність першого й останнього об’єктів у ланцюжку порівнянь).

ОЗНАЧЕННЯ 2.31. Еквівалентністю називається відношення Р, яке є водночас рефлексивним, симетричним та транзитивним.

Отже, еквівалентність – це толерантність, що має властивість транзитивності.

Якщо на площині означено множину векторів, то еквівалентними будуть вектори однакової довжини. Аналогічно, для множини фігур на площині можна вважати, що дві фігури А та В еквівалентні, якщо вони мають рівну площу.

В багатьох випадках відношення еквівалентності Р на довільній множині А означають таким способом.

Нехай задано відображення f: А ® B множини А в деяку множину В; будемо вважати хРу тоді й лише тоді, коли f(х) = f(y).

ОЗНАЧЕННЯ 2.32. Квазіпорядком називається відношення Р, яке є водночас рефлексивним та транзитивним.

Відношення квазіпорядку виникає в разі порівняння декількох альтернатив за векторним критерієм якості.

Приклад 2.23. Нехай А – носій відношення Р, і для кожного елемента хÎА означено множину з m кількісних характеристик. Цьому відповідає наступна реальна ситуація. Нехай А – множина альтернатив, і якість кожної з них вимірюється вектором кількісних критеріїв . Відношення Р можна задати наступним чином: для х,уÎА хРу тоді й лише тоді, коли виконується така умова:

(тобто хРу тоді й лише тоді, коли ).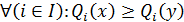

Це відношення є транзитивним та рефлексивним (тому що відношення «³» транзитивне та рефлексивне на множині дійсних чисел, значення із якої мають критерії), тобто є квазіпорядком.

Відношення Р лінійне, коли m = 1, тобто є лише один критерій. В інших випадках лінійність – це виняток, зумовлений специфікою носія, чим і пояснюються принципові труднощі прийняття рішень для задач із багатьма критеріями.

ОЗНАЧЕННЯ 2.33. Порядком називається відношення Р, яке є водночас рефлексивним, антисиметричним та транзитивним.

У прикладі 2.23 квазіпорядок перетворюється на порядок, коли для різних альтернатив хоча б один критерій має різні значення.

Щоб наголосити, що не всі пари елементів множини А порівняльні за відношенням порядку, деякі автори вживають термін «частковий порядок» (в англомовній літературі використовують абревіатуру «poset» від «partially ordered set»). Так, порядком буде впорядкування множини людей за відношенням «бути нащадком».

ОЗНАЧЕННЯ 2.34. Строгий порядок – це відношення Р, яке є водночас асиметричним та транзитивним.

Якщо R – порядок із носієм А, то йому можна поставити у відповідність строгий порядок Р наступним чином: (х,у)ÎР тоді й лише тоді, коли . Справедливе й обернене твердження: якщо Р – строгий порядок, то йому можна поставити у відповідність такий порядок R: (х,у)ÎR тоді й лише тоді, коли . Отже, строгий порядок не рефлексивний, а антирефлексивний.

ОЗНАЧЕННЯ 2.35. Лінійним порядком називають відношення Р, яке є водночас рефлексивним, антисиметричним, транзитивним та зв’язним.

Якщо Р – лінійний порядок, то 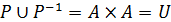, тобто об’єднання лінійного порядку з оберненим відношенням дорівнює повному відношенню. Саме в такому вигляді поняття лінійного порядку запровадив у 1895 р. Георґ Кантор.

Так, відношення «<» на множині чисел, лексикографічне впорядкування слів у словнику є лінійним порядком. На множині з n елементів можна задати n! різних лінійних порядків.

Із поняттям транзитивного замикання тісно пов’язане поняття досяжності.

ОЗНАЧЕННЯ 2.36. Досяжністю для довільного відношення Р називається найменше з відношень квазіпорядку, яке містить у собі відношення Р.

Інакше кажучи,

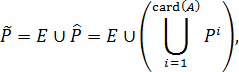
де Е – діагональне відношення, А – носій відношення.

Матриця досяжності має 1 на головній діагоналі, а відповідний граф – петлі при кожній вершині, оскільки будь–яка вершина графа досяжна сама із себе, тобто відношення досяжність рефлексивне. Відношення досяжності відображається наявністю шляху в графі G(P), тобто (де а,b Î А) тоді й лише тоді, коли в графі G(P) відношення Р існує шлях з вершини а до вершини b.

ОЗНАЧЕННЯ 2.37. Взаємною досяжністю 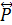для довільного бінарного відношення Р називається симетрична складова відповідного відношення досяжності ,

.

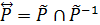Отже, 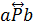тоді й лише тоді, коли в графі G(P) відношення Р є як шлях із вершини а до вершини b, так і шлях із b до а, тобто вершини а та b належать контуру в графі G(P).

Структуру відношення 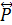розкриває таке твердження.

ТВЕРДЖЕННЯ 2.9. Симетрична складова відношення квазіпорядку є відношенням еквівалентності.

Доведення. Нехай Р – відношення квазіпорядку з носієм А. Оскільки за означенням це відношення рефлексивне, то для всіх хÎА правдиві твердження та 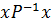, тому – також рефлексивне відношення. Відношення 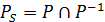симетричне за означенням як симетрична складова відношення Р. Оскільки відношення Р транзитивне, а– його симетрична складова, то згідно з властивістю транзитивних відношень P_S – теж транзитивне відношення (твердження 2.8). Отже, симетрична складова квазіпорядку рефлексивна, симетрична та транзитивна, тобто є еквівалентність.

Оскільки за означенням досяжність є квазіпорядком, то її симетрична складова – відношення взаємної досяжності – згідно з твердженням 2.9 є еквівалентністю. Для класів еквівалентності відношення 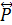існує важлива для практичних застосувань змістовна інтерпретація: дві різні вершини графа G(P) відношення Р належать до одного класу еквівалентності відношення 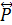тоді й лише тоді, коли існує контур у графі G(P), до якого належать ці вершини. Клас еквівалентності утворюють всі вершини контуру. Унаслідок того, що 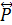– симетрична складова відношення досяжності , справедливе твердження 2.10.

ТВЕРДЖЕННЯ 2.10. Відношення Р ациклічне тоді й лише тоді, коли його відношення досяжності антисиметричне, тобто — відношення порядку.

Із цього твердження випливає, що для ациклічного відношення Р . Нехай Р — довільне відношення. Коли в його графі G(P) немає контурів, то воно антисиметричне (якщо аРb та bРа і відношення антисиметричне, то а = b). Якщо відношення Р транзитивне, то справедливе й обернене твердження. Справді, коли в цьому разі для х₁, х₂, ..., х_n Î А виконуються співвідношення х₁Pх₂, х₂Pх₃, ..., х_nPх₁, то внаслідок транзитивності відношення Р для довільного х_k водночас х₁Рх_k та х_kРх₁, що суперечить антисиметричності відношення Р. Необхідну та достатню умову транзитивності лінійних відношень дає твердження 2.11.

ТВЕРДЖЕННЯ 2.11. Якщо граф лінійного відношення немає контурів, то воно транзитивне.

Доведення.Нехай у графі відношення Р з носієм А немає контурів. Розглянемо такі а, b, с Î А, що аРb, bРс, а ¹ b ¹ с. Припустімо, що 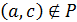. Тоді внаслідок лінійності відношення Р повинно виконуватися сРа, тобто аРb, bРс, сРа. Це й означає, що в графі G(P) відношення Р існує контур (а, b, с), що суперечить умові. Отже, відношення Р є транзитивним.¨

Наведені результати широко використовують, досліджуючи властивості бінарних відношень, отриманих здебільшого експериментально як результат опитування децидентів–експертів у різноманітних ситуаціях прийняття рішень [5]. Доведені твердження дають можливість побудувати алгоритми перевірки експериментальних відношень на наявність таких важливих властивостей, як транзитивність, ациклічність, лінійність та ін. Це, у свою чергу, допомагає виявити та скорегувати суперечності в поведінці децидента і можливі аномальні ситуації прийняття рішень.

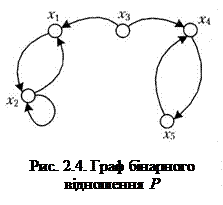Приклад 2.24. Розглянемо таке відношення Р (рис. 2.4):

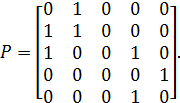
Знайдемо його транзитивне замикання.

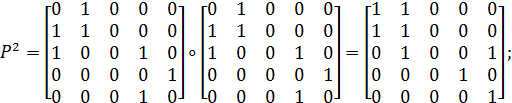
Оскільки Р³ = Р⁵, то

Знайдемо відношення досяжності :

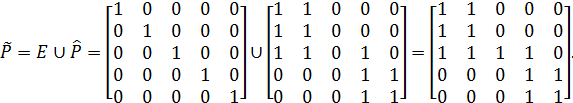
Визначимо відношення взаємної досяжності :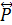

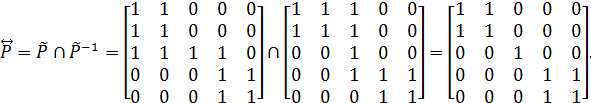
Еквівалентність 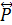розбиває множину–носія А відношення Р на три класи еквівалентності: A₁ = {x₁, х₂}, A₂ = {х₃}, А₃ = {х₄, х₅}, що означає наявність у графі G(P) двох контурів – до одного входять вершини з множини А₁ до другого – з множини А₃.

Таким чином, позаяк інформацію про систему переваг децидента найчастіше одержують, опитуючи децидента чи спостерігаючи, коли він вибирає варіант дій із множини можливих, і виникає проблема перевірки отриманого бінарного відношення на наявність певних бажаних властивостей. Розглянуті властивості дають змогу визначити цікаві з погляду ТПР відношення: толерантності, еквівалентності, квазіпорядку та ін. – а також дослідити важливі практичні ситуації прийняття рішень, що приводять до цих відношень.

Читайте також:

1. III. Сприйняття й засвоєння учнями навчального матеріалу
2. IV. Прийняття рішень у полі четвертої інформаційної ситуації
3. IV. Сприйняття та усвідомлення навчального матеріалу
4. V. Прийняття рішень у полі п’ятої інформаційної ситуації
5. VI. Прийняття рішень у полі шостої інформаційної ситуації
6. А .Маршалл - основоположник неокласичної теорії.
7. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
8. Алгоритм прийняття рішення при прийманні сигналів з випадковою початковою фазою
9. Альтернативні теорії вартості
10. Альтернативні теорії капіталу
11. Альтернативні теорії макроекономічного регулювання
12. Альтернативні теорії максимізації

Переглядів: 3627