• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Властивості бінарних відношень

Властивості та основні типи бінарних відношень

У теорії прийняття рішень використовують певні типи бінарних відношень із конкретними властивостями. Один із підходів полягає у формулюванні властивостей бажаного відношення у формі аксіом із подальшим пошуком конструктивного методу побудови такого відношення чи класу відношень або ж доведення неможливості його існування, якщо сформульована система аксіом суперечлива [25].

Основні властивості відношень – рефлексивність, антирефлексивність, симетричність, асиметричність, антисиметричність, транзитивність і ациклічність.

ОЗНАЧЕННЯ 2.22. Рефлексивним називається таке відношення Р, для якого справедливе твердження Е Í Р, де Е – діагональне відношення.

Це означає, що для всіх хÎА, де А – носій відношення Р, хРх. У матриці рефлексивного відношення на головній діагоналі завжди стоять 1, а у відповідному графі при кожній вершині є петля.

ОЗНАЧЕННЯ 2.23. Антирефлексивним називається відношення Р, для якого .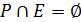

Таким чином, для всіх 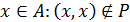, тобто в матриці відношення на головній діагоналі завжди стоять 0, а в графі – немає петель.

ОЗНАЧЕННЯ 2.24. Симетричним називається відношення Р, для якого .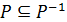

Для всіх х, yÎА, які перебувають у такому відношенні Р, тобто хРу, справедливе твердження уРх. У матриці симетричного відношення елементи b_ij та b_ji розміщені симетрично відносно головної діагоналі, рівні між собою. У графі G(P) наявність дуги (x_i, x_j) означає, що є і дуги (х_j, х_i).

ОЗНАЧЕННЯ 2.25. Асиметричним називається відношення Р, для якого 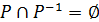, тобто якщ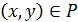о , то .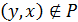

У матриці такого відношення 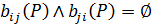для всіх і та j, а на головній діагоналі знаходяться 0. У графі G(P) немає водночас дуг (х_i, х_j) та (x_j, х_i), а також петель.

ОЗНАЧЕННЯ 2.26. Антисиметричним називається відношення Р, якщо , де Е – діагональне відношення.

Отже, твердження хРу та уРх справедливі водночас лише тоді, коли х = у. У матриці В(Р) умова 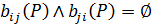виконується для всіх і, j, окрім і = j. У графі G(P) немає водночас дуг (х_i, х_j) та (x_j, х_i), але можуть бути петлі.

Приклад 2.20. Розглянемо відношення Р, Q, R:

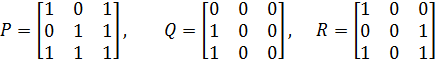
Відношення P симетричне та рефлексивне, Q – антирефлексивне і асиметричне, R – антисиметричне, що перевіряється безпосередньо за означеннями цих властивостей:

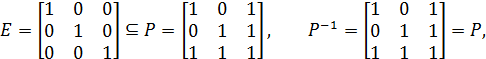
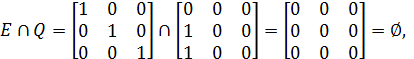
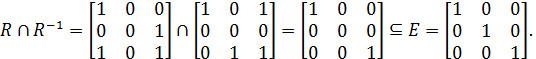
Приклад 2.21. Розглянемо приклади відношень із наведеними вище властивостями.

Відношення між об’єктами «бути подібним», «бути не молодшим» рефлексивні, тому що об’єкт подібний на самого себе (тотожний сам собі), людина не молодша за саму себе.

Відношення «відрізнятися», «бути молодшим», «бути батьком» не рефлексивні. Більше того, вони антирефлексивні (тому що об’єкт не може відрізнятися від самого себе, бути молодшим за самого себе чи бути батьком самому собі).

Відношення «бути родичем» симетричне (якщо А – родич В, то і В – родич А), «бути батьком» – асиметричне (якщо А – батько В, то В не батько А).

Відношення «бути сестрою» не симетричне і не асиметричне. Так, якщо Марія – сестра Ольги, то Ольга – сестра Марії, але якщо Марія – сестра Петра, то, звичайно ж, Петро – не сестра Марії.

Відношення «³» на множині дійсних чисел антисиметричне.

ОЗНАЧЕННЯ 2.27. Транзитивним називається відношення, для якого 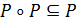, тобто якщо xPz і zPy, то хРу.

За індукцією як наслідок отримуємо: якщо xPz₁, z₁Pz₂, ..., z_nPy, то хРу. У матриці В(Р) транзитивного відношення для довільних значень і, k виконується співвідношення

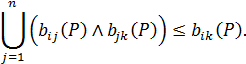
У графі G(P) транзитивного відношення Р якщо існує шлях з x в у, то існує дуга (х, у).

Із поняттям транзитивного відношення тісно пов’язане поняття операції транзитивного замикання. Для кожного відношення Р означимо відношення 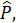як мінімальне транзитивне відношення, у якому міститься відношення Р. Його однозначно означають як 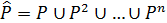, де n = саrd(A), А – носій відношення Р, a card(A) – потужність множини А.

Приклад 2.22. Знайдемо транзитивне замикання відношення

.

,

,

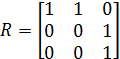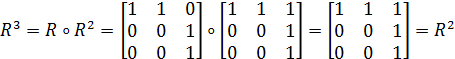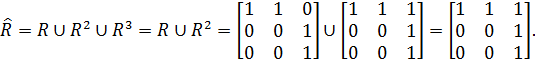
ОЗНАЧЕННЯ 2.28. Ациклічним називається відношення Р, для якого 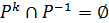для довільного k.

Для ациклічного відношення з xPz₁, z₁Pz₂, ..., z_nPy випливає х ¹ у, тобто якщо в графі G(P) ациклічного відношення Р вершини х та у з’єднані шляхом, то в ньому немає дуги (у, х).

Ациклічність і транзитивність – важливі властивості для ТПР, вони відображають певні природні взаємозв’язки між об’єктами. Якщо об’єкт х у певному розумінні кращий за у, а у кращий за z, то природно вважати, що об’єкт х кращий, ніж z (транзитивність), і щонайменше об’єкт z не кращий за х (ациклічність).

ОЗНАЧЕННЯ 2.29. Зв’язним відношенням називається відношення Р, для якого 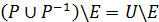, де 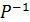– обернене до Р відношення, U – повне, Е – діагональне.

Це означає, що для довільних елементів х, у Î А, х ¹ у, де А – носій відношення Р, чи (х,у) Î Р, чи (у, х) Î Р. У матриці В(Р) хоча б один з елементів b_ij, b_ji дорівнює 1, а граф G(P) зв’язний.

Доведемо декілька тверджень, які стосуються взаємозв’язків між властивостями відношень.

ТВЕРДЖЕННЯ 2.1. Відношення Р симетричне тоді й лише тоді, коли .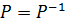

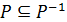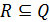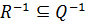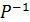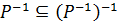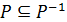Доведення. За означенням для симетричного відношення . Оскільки для довільних відношень R і Q з випливає , то підставивши замість R відношення Р, а замість Q – , отримаємо , або . Оскільки водночас та , то . ¨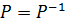

ТВЕРДЖЕННЯ 2.2. Якщо відношення Р асиметричне, то воно антирефлексивне.

Доведення. Нехай для хÎА, де А – носій відношення Р, виконується хРх. За означенням оберненого відношення це означає, що 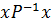. Однак тоді 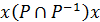, що суперечить припущенню про асиметричність відношення Р. ¨

ТВЕРДЖЕННЯ 2.3. Якщо відношення Р та Q симетричні, то симетричні й відношення .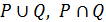

Доведення. За твердженням 2.1, 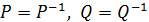. Виходячи з справедливості співвідношення 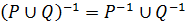, отримаємо 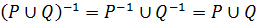, що і доводить твердження. Аналогічно . ¨

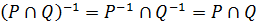ТВЕРДЖЕННЯ 2.4. Композиція симетричних відношень Р та Q симетрична тоді й лише тоді, коли .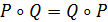

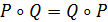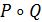Доведення. Нехай . Тоді , тобто композиція симетрична, що доводить достатність умови комутативності.

Нехай відношення 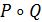симетричне. Тоді . Позаяк відношення Р та Q симетричні, то 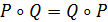, що й доводить необхідність умови комутативності. ¨

ТВЕРДЖЕННЯ 2.5. Відношення 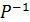обернене до транзитивного відношення Р, є транзитивним.

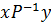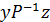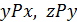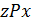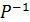Доведення. Нехай Р – транзитивне відношення, й та . Тоді , і внаслідок того, що Р – транзитивне відношення, , тобто . Отже, відношення транзитивне. ¨

ТВЕРДЖЕННЯ 2.6. Перетин довільної кількості транзитивних відношень з одним і тим самим носієм є транзитивним відношенням.

Доведення. Розглянемо множину транзитивних відношень {Р_i}, iÎІ, з носієм А. Нехай хРу, yPz. Це означає, що для довільного iÎІ виконується хР_iу, yP_iz.

Оскільки відношення Р_i транзитивне, то хР_iz. Оскільки хР_iz виконується для довільного iÎІ, це означає, що

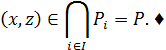
Для операції об’єднання подібне твердження неправильне. Це має глибокий прикладний сенс: якщо ми хочемо побудувати результуюче групове відношення, за умови транзитивності відношення кожного з експертів, то після об’єднання властивість транзитивності результуючого відношення зникає.

Результуюче відношення, отримане об’єднанням транзитивних відношень, також транзитивне, якщо виконуються деякі додаткові умови. Уведемо поняття транзитивності одного відношення щодо іншого. Відношення Р називатимемо транзитивним стосовно відношення Q, якщо з хРуÙyQz випливає xPz, а з xQyÙyPz — xPz.

Неважко довести твердження 2.7 і 2.8, що визначають умови транзитивності.

ТВЕРДЖЕННЯ 2.7. Якщо два відношення транзитивні й одне з них транзитивне відносно іншого, то об’єднання цих відношень транзитивне.

Нехай Р — довільне бінарне відношення. Відношення 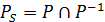називається симетричною складовою відношення Р, а 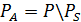— його асиметричною складовою.

ТВЕРДЖЕННЯ 2.8. Нехай Р – транзитивне відношення. Тоді його симетрична складова P_S і асиметрична складова Р_А транзитивні. А відношення Р_А транзитивне відносно P_S.

Читайте також:

1. Аеродинамічні властивості колісної машини
2. Аналізатори людини та їхні властивості.
3. Аналізатори людини та їхні властивості.
4. Атрибутивні ознаки і властивості культури
5. Білки, властивості, роль в життєдіяльності організмів.
6. Біосфера Землі, її характерні властивості
7. Будова атомів та хімічний зв’язок між атомами визначають будову сполук, а отже і їх фізичні та хімічні властивості.
8. Будова і властивості аналізаторів
9. Векторний добуток і його властивості.
10. Вибір кращих альтернатив за допомогою бінарних відношень
11. Види і властивості радіоактивних випромінювань
12. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).

Переглядів: 5542