• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Ізоморфізм, гомоморфізм і двоїстість бінарних відношень

Зв’язок між відношеннями, означеними на різних множинах, описують у термінах ізоморфізму та гомоморфізму.

ОЗНАЧЕННЯ 2.19. Відношення Р з носієм А (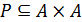) та Q з носієм С (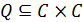) називаються ізоморфними, якщо існує таке взаємно однозначне відображення

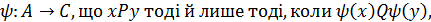
де хÎА, уÎА, y(х)ÎС, y(y)ÎС.

ОЗНАЧЕННЯ 2.20. Гомоморфним називається однозначне відображення відношення Р з носієм А в відношення Q з носієм С, тобто існує однозначне відображення множини А в множину С

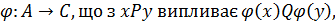
де хÎА, уÎА, j(х)ÎС, j(y)ÎС.

Приклад 2.17. Розглянемо відношення 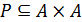, де А = {х₁, х₂, х₃}, та 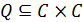, де C = {y₁, y₂, y₃}:

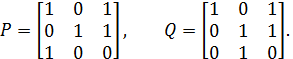
Відобразимо взаємно однозначно х₁ ® у₂, х₂ ® у₁, х₃ ® у₃, тобто у₂ = y(х₁), у₁ = y(х₂), у₃ = y(х₃), х₁ = y^–1(у₂), х₂ = y^–1(у₁), х₃ = y^–1(у₃). Прямою перевіркою впевнюємося, що для всіх хÎА і уÎА, y(х)ÎС, y(y)ÎС справедливе співвідношення

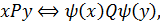
тобто відношення Р та Q ізоморфні.

Приклад 2.18. Розглянемо відношення 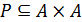з носієм А = {х₁, х₂, х₃, х₄, х₅} та 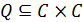з носієм C = {y₁, y₂, y₃}, подані матрицями:

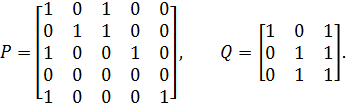
Однозначне відображення Р в Q породжується таким відображенням j: А ® С:

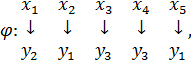
для якого справедливе твердження 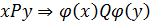для всіх значень хÎА, уÎА, j(х)ÎС, j(y)ÎС. Обернене відображення багатозначне (наприклад, ). Отже, j гомоморфно відображає відношення Р у відношення Q.

У теорії вибору, побудованій на бінарних відношеннях, велике значення має поняття двоїстого відношення.

ОЗНАЧЕННЯ 2.21. Двоїстим до відношення Р називається відношення

Щоб перейти від графа G(P) до графа G(P^d), потрібно виконати такі дії:

v видалити з нього всі пари протилежних дуг і петлі;

v додати пари протилежних дуг для тих вершин, які в графі G(P) не були зв’язані дугою;

v додати петлі при тих вершинах, де їх не було в графі G(P).

Для двоїстих відношень виконуються такі співвідношення:

Основні дії над бінарними відношеннями можна наочно інтерпретувати, зображаючи їх у вигляді графів. Так, граф доповнення 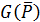до відношення Р складається з тієї самої множини вершин, що й граф G(P), але в ньому є ті й лише ті дуги, яких немає в графі G(P); граф G(P^–1) можна отримати з графа G(P), змінивши напрямки всіх дуг, і т.ін.

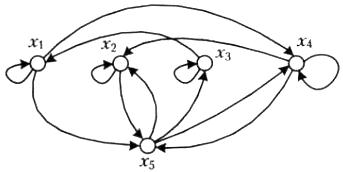
Приклад 2.19. Задано відношення Р з носієм А = {х₁, х₂, х₃, х₄} та його граф G(P) (рис. 2.2). Відповідне двоїсте відношення та його граф G^–1(P) матимуть такий вигляд, як на рис. 2.3.

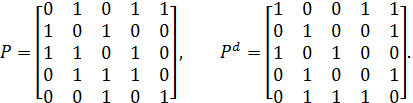
Згідно з означеннями основних дій над бінарними відношеннями наведемо формули для отримання відповідних елементів матриці В(n×n):

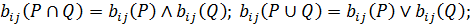
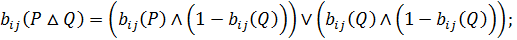
Рис. 2.2. Граф прямого відношення	Рис. 2.3. Граф двоїстого відношення

Наведемо також іще кілька корисних співвідношень для довільних бінарних відношень зі спільним носієм А:

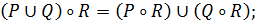
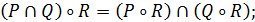
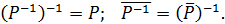
Їх можна легко довести, використовуючи означення дій над відношеннями та матричне їх подання.

Отже, переваги децидента досліджують за допомогою основних типів бінарних відношень.

Читайте також:

1. Вибір кращих альтернатив за допомогою бінарних відношень
2. Відхилення від типових чисельних співвідношень і їх причини.
3. Властивості бінарних відношень
4. Властивості факторизованих відношень
5. Встановлення відношень між судженнями за правилами логічного квадрата.
6. Гомоморфізми та ізоморфізми алгебр
7. ДО ПРОБЛЕМИ ОБ’ЄКТНИХ ВІДНОШЕНЬ У ПСИХОЛОГІЇ
8. Елементарні типи бінарних відношень
9. Ізоморфізм та гомоморфізм алгебр
10. Існування тричленних похідних співвідношень
11. Метод рекурентних співвідношень. Використання принципу Беллмана і алгоритму Джонсона.

Переглядів: 1550