• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Питання

3.1 Зміст другого закону термодинаміки

3.2 Змінення ентропії у основних термодинамічних процесах

3.3 Статистичне тлумачення другого закону термодинаміки

3.1 Зміст другого закону термодинаміки

Усі процеси, які можна уявити, поділяються на самодовільні, несамодовільні та рівноважні. У природі, що нас оточує, постійно спостерігається самодовільне, однобічне проходження природних процесів. Так, теплота завжди переходить від більш нагрітого тіла до менш нагрітого, рідина завжди прагне зайняти найнижчий рівень, гази прагнуть завжди розширитися тощо. І ці процеси самодовільно проходять доти, поки у системі не встановиться рівновага. Експериментально доведено, що самодовільного проходження цих процесів у зворотному напрямку не відбувається, тобто ці процеси незворотні.

Процеси, зворотнісамодовільним, називаютьсянесамодовільними.Вони можуть проходити тільки при витрачанні енергії ззовні або у сполученні з самодовільними процесами всередині системи. У результаті несамодовільного процесу система віддаляється від стану рівноваги.

Перший закон термодинаміки не дозволяє передбачити, чи буде даний процес самодовільним або несамодовільним. Так, самодовільний перехід теплоти від холодного тіла до гарячого не заперечує першому закону термодинаміки. Йому не заперечують і такі процеси, як самодовільне розподілення розчину на складові його речовини або самодовільне стиснення газів.

На питання про те, буде проходити чи ні даний процес, наприклад хімічна реакція, самодовільно, якими параметрами буде характеризуватися система, коли вона перейде у стан термодинамічної рівноваги, можна отримати відповідь за допомогою другого закону термодинаміки.

Другий закон термодинаміки дозволяє логічним шляхом створити струнку систему співвідношень між параметрами стану системи, за допомогою яких можна отримати не тільки відповіді на зазначені питання, але й цілий ряд інших фундаментальних результатів, які відіграють важливу роль у фізичній хімії, фізиці, техніці.

Основний зміст другого закону термодинаміки полягає у ствердженні існування ентропіїта її незменшення в ізольованій системі. Історично він був отриманий спочатку в результаті аналізу роботи теплових машин.

Запропоновано багато різних формулювань другого закону термодинаміки. Усі вони рівноцінні одне одному та можуть бути виведені логічно одне з іншого. Одне з формулювань другого закону термодинаміки (постулат Клаузиуса) звучить так:

єдиним результатом будь-якої сукупності процесів не може бути перехід теплоти від холодного тіла до гарячого.

Це ствердження за своєю суттєвістю еквівалентне такому (постулат Томпсона):

теплота найхолоднішого з тіл, що беруть участь у процесі, не може бути джерелом роботи.

Формулювання Оствальдастверджує, що

неможливе створення вічного двигуна другого роду.

Вічний двигун другого роду це теплова машина, що виконує роботу тільки за рахунок поглинання теплоти із навколишнього середовища, але не передає частини її іншим тілам. При роботі такої машини закон збереження енергії не порушується, але створення такої машини неможливе.

Нарешті, можна сформулювати другий закон термодинаміки, постулюючи існування деякої функції стану системи, що називається ентропією (S):

існує функція стану системи (S), змінювання якої таким чином пов¢язане із поглинутою теплотою та температурою системи:

dQ<TdS – для самодовільних процесів,

dQ=TdS – для оборотних процесів,

dQ>TdS - для несамодовільних процесів.

Звідси випливає, що в ізольованих системах, в яких можливі тільки самодовільні або оборотні процеси, ентропія не може зменшуватися, тобто dS ³ 0.

3.2 Змінення ентропії у основних термодинамічних процесах

Змінення ентропії у зворотному та незворотному процесах однакове, оскільки ентропія є функцією стану системи. Отже, щоб обчислити зміни ентропії у даному реальному процесі, треба цей процес подумки поділити на стадії, що проходять зворотно, та обчислити для них зміни ентропії за рівнянням для зворотних процесів. Взявши суму зміни ентропії на всіх стадіях, отримуємо зміни ентропії у реальному процесі (зворотному або незворотному).

Обчислимо змінювання ентропії для різних процесів, ураховуючи, що dS = dQ/T:

1) Ізотермічний процес (Т = const).

dQ_T = PdV i dS_T = PdV/T.

Звідси

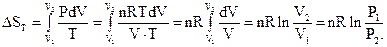(3.1)

Для фазового перетворення (плавлення, випарювання, кристалізація тощо), що завжди проходить при постійній температурі, можна отримати

DS_ф.п = DН_ф.п /Т_ф.п (3.2)

де DН_ф.п – теплота фазового переходу; Т_ф.п – температура фазового переходу.

2) Ізохоричний процес ( V = const).

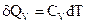i

Звідси

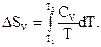(3.3)

Для ідеального газу (С_V = const)

(3.4)

3) Ізобаричний процес (Р = const).

i .

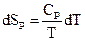Звідси

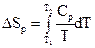. (3.5)

Для ідеального газу ( С_Р = const)

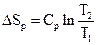. (3.6)

4) Адіабатичний процес.

В адіабатичному процесі dQ = 0. Тому dS = 0 і

S = const (3.7)

Таким чином, адіабатичний рівноважний процес можна назвати ізоентропійним.

5) Зміни ентропії ідеального газу.

Для зворотного процесу з ідеальним газом, в якому єдиним видом роботи є робота сил розширення, можна записати

dQ = dU + PdV = nC_VdT + PdV (3.8)

Далі

(3.9)

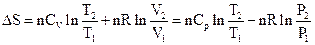(3.10)

Для розрахунку зміни ентропії 1 моль індивідуальної речовини з урахуванням можливих фазових переходів використовують співвідношення

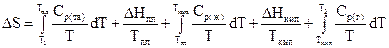(3.11)

Якщо у твердому стані речовина має більше однієї кристалічної модифікації, треба додати відповідні складові до правої частини рівняння.

На відміну від внутрішньої енергії та ентальпії для ентропії можна визначити абсолютні значення. Ця можливість не випливає з другого закону термодинаміки, а з¢являється лише при використанні постулату Планка, відомого як третій закон термодинаміки.

3.3 Статистичне тлумачення другого закону термодинаміки

Статистичний або ймовірнісний характер другого закону термодинаміки був відкритий Больцманом. Він вивів зв¢язок між ентропією та ймовірністю існування системи. Розглянемо спочатку поняття термодинамічної ймовірності.

Стан системи можна характеризувати значеннями термодинамічних параметрів – енергією, об¢ємом, тиском тощо. Ці параметри характеризують систему в цілому, тому вони визначають, як кажуть, макростансистеми. Можна також описати систему, відмічаючи положення кожної частинки та її енергію. Визначеному значенню цих величин відповідає мікростансистеми. Одному макростану системи може відповідати безліч мікростанів. Наприклад, якщо даний макростан характеризується енергією Е, то вона може бути розподілена між N частинками різними способами. Так, якщо N₁ частинок мають енергію e₁ кожна, N₂ – енергію e₂ тощо, то

Е = N₁e₁ + N₂e₂ + N₃e₃ + N₄e₄ + …

Одному й тому самому значенню Е може відповідати різне розподілення частинок за енергіями, тобто різні мікростани.

Термодинамічна ймовірність W даного макростану дорівнює кількості мікростанів, відповідних цьому макростану.

Для розрахунку термодинамічної ймовірності використовують формулу:

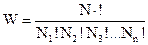(3.12)

Розглянемо як приклад дві однакові частинки у ящику, розподіленому на дві частини. Усі можливі розподілення цих частинок на два відділення наведені на рис.3.1. Кожне розподілення є мікростаном системи. При рівномірному розподіленні частинок термодинамічна ймовірність W = 2, оскільки двом мікростанам відповідає один макростан. Для випадків а і г W=1.

Природно припустити, що за відсутності перегородки буде реалізований рівномірний розподіл частинок по всьому ящику. Такий розподіл більш ймовірний.

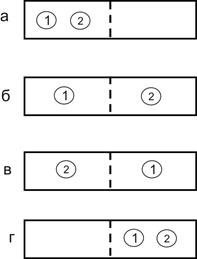
Рисунок 3.1 – Система з двох частинок

Зі статистичної точки зору другий закон термодинаміки може бути сформульований так:

самодовільні процеси проходять від менш ймовірних до більш ймовірних.

Оскільки при проходженні в ізольованій системі самодовільних незворотних процесів збільшується ентропія системи, то, очевидно, ентропія і термодинамічна ймовірність є взаємопов¢язаними величинами. Знайдемо цей зв¢язок.

Покладемо, що є дві системи, які мають ентропії S₁ i S₂ та термодинамічні ймовірності W₁ i W₂. Поєднуючи ці системи в одну, можна стверджувати, що термодинамічна ймовірність її буде дорівнювати добутку ймовірностей W₁₂ = W₁×W₂ ( на підставі теорії ймовірності), а ентропія її – сумі ентропій S₁₂=S₁+S₂ (на підставі властивості адитивності ентропії). Звідси, враховуючи, що S₁ = S (W₁), S₂ = S(W₂), S₁₂ = S(W₁₂) = =S(W₁×W₂), можна записати

S(W₁×W₂) = S(W₁) + S(W₂) (3.13)

Продиференціювавши цей вираз спочатку по W₁ (при W₂=const), а потім по W₂ (при W₁ = const), отримуємо

W₂S¢(W₁×W₂) = S¢(W₁) , W₁S¢(W₁×W₂) = S¢(W₂) (3.14)

Помноживши перше рівняння на W₁, а друге на W₂, отримуємо

W₁W₂S¢(W₁×W₂) = S¢(W₁)W₁, W₁W₂S¢(W₁×W₂) = S¢(W₂)W₂.

Прирівнявши праві частини цих рівнянь, маємо

S¢(W₁)W₁ = S¢(W₂)W₂

або S¢(W)×W = const = k (3.15)

Звідси

(3.16)

З іншого боку, із S = S(W) маємо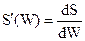. Порівнюючи вирази, отримуємо

(3.17)

Інтегрування дає

S = klnW + const (3.18)

Значення постійної інтегрування, як було встановлено Планком, може бути прирівняне до нуля, а коефіцієнт пропорційності k у наведеній формулі є сталою Больцмана. Таким чином, рівняння (рівняння Больцмана), що пов¢язує ентропію з термодинамічною ймовірністю, набуває вигляду

S = k lnW (3.19)

Статистичний характер другого закону термодинаміки дозволяє тлумачити ентропію як міру невпорядкованості системи. Повний порядок у системі спостерігається, коли розміщення кожного об¢єкта, що входить у систему, суворо визначено, отже, може бути тільки один мікростан, що відповідає макростану системи.

Найбільший безлад спостерігається у газоподібних речовинах. Для них термодинамічна ймовірність та ентропія найбільші. Порядок збільшується при переході до рідини та ще більше – до кристалу. Так, ентропія одного моля води у твердому стані дорівнює 43,9 Дж/моль×К, у рідкому стані – 66,9 Дж/моль×К та у газоподібному – 188,7 Дж/моль×К. Безумовно, мінімальне значення ентропії має кристал при нулі градусів за Кельвіном.

У більшості випадків виконується правило – чим твердіша речовина, тим нижча її ентропія. Так, стандартна ентропія алмазу складає 2,439 Дж/моль×К, а графіту – 5,694 Дж/моль×К.

Із статистичного тлумачення ентропії випливає, що збільшення ентропії ізольованої системи відображає тільки найбільш ймовірне проходження реальних процесів, перехід системи з менш ймовірного стану у більш ймовірний. Однак статистичне тлумачення ентропії не виключає можливості переходу системи з більш ймовірного у менш ймовірний стан, тобто не виключає можливості процесів, що супроводжуються зменшенням ентропії ізольованої системи, хоча ймовірність таких процесів дуже мала. Наприклад, розрахунки польського вченого М.Смолуховського показують, що коли ми маємо один кубічний сантиметр газу при нормальних умовах, то тільки 1 раз протягом 10¹⁴⁰ років можна спостерігати 1 % відхилення щільності газу від рівноважного значення.

3.4 Залежність ентропії хімічної реакції від температури

Для розрахунку ентропії хімічної реакції для стандартної температури слід скористатися правилом, аналогічним правилу для розрахунку ентальпії хімічної реакції, а саме

Ентропія хімічної реакції дорівнює різниці стандартних ентропій продуктів реакції і стандартних ентропій вихідних речовин з урахуванням коефіцієнтів перед речовинами в рівнянні реакції.

Так, для реакції n N + m M = k K + d D

DS₂₉₈ = [kS⁰₂₉₈(K)+dS⁰₂₉₈(D)] - [nS⁰₂₉₈(N)+mS⁰₂₉₈(M)] (3.20)

Розрахунок ентропії хімічної реакції для нестандартної температури проводять за рівнянням, висновок якого аналогічний висновку рівняння Кірхгофа (2.14)

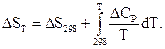(3.21)

Це рівняння, як і рівняння Кірхгофа може використовуватися в трьох наближеннях. У першому наближенні приймають DС_Р=0, тобто вважають рівними теплоємності початкових і кінцевих речовин. Отримують DS_Т =DS₂₉₈.

При використанні другого наближення вважають, що DС_Р не залежить від температури. У цьому випадку розраховують DС_Р для стандартної температури за загальноприйнятою методикою, а рівняння (3.21) перетворюється на

DS_Т = DS₂₉₈ + DС_рln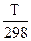 (3.22)

Третє наближення базується на використанні точної залежності теплоємностей речовин від температури: С_Р=а+bТ+сТ² + с¢/Т². У цьому випадку

DС_Р = Dа + DbТ + DсТ² + Dс¢/Т² (3.23)

Розрахунок Dа, Db, Dс, Dс¢ проводять як описано в лекції 2 розділ 2.4. Підставляючи (3.23) в рівняння (3.21), отримуємо

Або після інтегрування

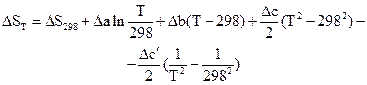(3.24)

Розрахунки за формулами 3.20, 3.22 і 3.24 для реакції

2SO₂(г)+O₂(г)=2SO₃(г)

для Т = 928К привели відповідно до таких результатів:

DS₂₉₈=-187,80Дж/мольК,

DS₉₂₈=-177,66Дж/мольК,

DS₉₂₈=184.95Дж/мольК.

Висновки

Розглянуто зміст і формулювання другого закону термодинаміки. Наведени математичні формули для розрахунку ентропії в основних термодинамічних процесах. Докладно розглянуто імовірнісний зміст другого закону термодинаміки і зроблений висновок про те, що можливо перебіг будь-яких процесів.

СТИСЛИЙ конспект лекцІй

Усі процеси, які можна уявити, поділяються на самодовільні, несамодовільні та рівноважні. У природі, що нас оточує, постійно спостерігається довільне, однобічне проходження природних процесів. Так, теплота завжди переходить від більш нагрітого тіла до менш нагрітого, рідина завжди прагне зайняти найнижчий рівень, гази прагнуть завжди розширитися тощо.

Процеси, зворотнісамодовільним, називаютьсянесамодовільними.У результаті несамодовільного процесу система віддаляється від стану рівноваги. І ці процеси довільно проходять доти, поки у системі не встановиться рівновага.

Основний зміст другого закону термодинаміки полягає у ствердженні існування ентропіїта її незменшення в ізольованій системі.

Запропоновано багато різних формулювань другого закону термодинаміки. Усі вони рівноцінні одне одному та можуть бути виведені логічно одне з іншого. Одне з формулювань другого закону термодинаміки (постулат Клаузиуса) звучить так:

єдиним результатом будь-якої сукупності процесів не може бути перехід теплоти від холодного тіла до гарячого.

Це ствердження за своєю суттєвістю еквівалентне такому (постулат Томпсона):

теплота найхолоднішого з тіл, що беруть участь у процесі, не може бути джерелом роботи.

Формулювання Оствальдастверджує, що

неможливе створення вічного двигуна другого роду.

Вічний двигун другого роду це теплова машина, що виконує роботу тільки за рахунок поглинання теплоти із навколишнього середовища, але не передає частини її іншим тілам.

Нарешті, можна сформулювати другий закон, постулюючи існування деякої функції стану системи, що називається ентропією (S):

існує функція стану системи (S), змінювання якої таким чином пов¢язане із поглинутою теплотою та температурою системи:

dQ<TdS – для самодовільних процесів,

dQ=TdS – для оборотних процесів,

dQ>TdS - для несамодовільних процесів.

Обчислимо змінювання ентропії для різних процесів, ураховуючи, що dS = dQ/T:

1) Ізотермічний процес (Т = const).

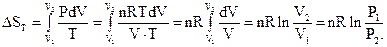
2) Ізохоричний процес ( V = const).

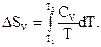
Для ідеального газу (С_V = const)

3) Ізобаричний процес (Р = const).

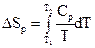
Для ідеального газу ( С_Р = const)

.

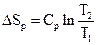4) Адіабатичний процес.

В адіабатичному процесі dQ = 0. Тому dS = 0 і

S = const

Таким чином, адіабатичний рівноважний процес можна назвати ізоентропійним.

Для розрахунку зміни ентропії 1 моль індивідуальної речовини з урахуванням можливих фазових переходів використовують співвідношення

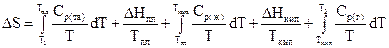
Статистичний або ймовірнісний характер другого закону термодинаміки був відкритий Больцманом. Стан системи можна характеризувати значеннями термодинамічних параметрів – енергією, об¢ємом, тиском тощо. Ці параметри характеризують систему в цілому, тому вони визначають, як кажуть, макростансистеми. Можна також описати систему, відмічаючи положення кожної частинки та її енергію. Визначеному значенню цих величин відповідає мікростансистеми. Одному макростану системи може відповідати безліч мікростанів.

Зі статистичної точки зору другий закон термодинаміки може бути сформульований так:

самодовільні процеси проходять від менш ймовірних до більш ймовірних.

Таким чином, рівняння, що пов¢язує ентропію з термодинамічною ймовірністю, набуває вигляду

S = k lnW

Статистичний характер другого закону термодинаміки дозволяє тлумачити ентропію як міру невпорядкованості системи.

Однак статистичне тлумачення ентропії не виключає можливості переходу системи з більш ймовірного у менш ймовірний стан, тобто не виключає можливості процесів, що супроводжуються зменшенням ентропії ізольованої системи, хоча ймовірність таких процесів дуже мала.

Розрахунок ентропії хімічних реакцій для стандартної і нестандартної температур може бути проведений за формулами:

DS₂₉₈ = [kS⁰₂₉₈(K)+dS⁰₂₉₈(D)] - [nS⁰₂₉₈(N)+mS⁰₂₉₈(M)],

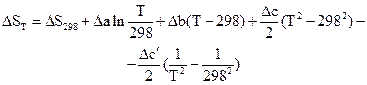
Ключові терміни

Другий закон термодинаміки; макростан; мікростан; термодинамічна ймовірність; рівняння Больцмана;ентропія хімічної реакції

Питання для самоперевірки

1. Наведіть приклади таких процесів, які: а) є самочинними; б) не є самочинними; в) є оборотними.

2. Порівняйте відомі Вам формулювання другого закону термодинаміки. Знайдіть спільне в цих формулюваннях.

3. Виведіть вирази для ентропії в основних термодинамічних процесах.

4. Дайте іншу назву адіабатичному процесу. Намалюйте графіки чотирьох основних термодинамічних процесів в координатах Т – S.

5. Виведіть рівняння Больцмана.

6. Дайте визначення мікро- і макростанам системи, термодинамічної ймовірності існування системи.

7. В яких межах може змінюватися термодинамічна ймовірность існування системи?

8. Поясніть ймовірнісний характер ентропії. Наведіть числові приклади.

9. Сформулюйте другий закон термодинаміки з урахуванням імовірнісного характеру ентропії.

10. Чи можливий перебіг самочинних процесів у зворотному напрямі?

Читайте також:

1. IV. Питання самоконтролю.
2. V. Питання для самоконтолю
3. V. Питання туристично-спортивної діяльності
4. VI . Екзаменаційні питання з історії української культури
5. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
6. Актуальні питання управління земельними ресурсами та їх охорони
7. Аналогія права - вирішення справи або окремого юридичного питання на основі принципів права, загальних засад і значення законодавства.
8. Бесіда за запитаннями.
9. В лекції висвітлюються питання використання мережних структур, їх недоліки та переваги.
10. Виділення в природних комплексах незвичайних, унікальних ділянок і явищ і питання їх збереження.
11. Висновок з 1 питання
12. Відповідаючи на питання, будьте впевнені в своїй перемозі і все у вас вийде.

Переглядів: 1300