Загальна схема дослідження функції і побудова її графіка

Графік заданої функції можна будувати по довільно взятих точках. При такому способі можна не виявити всіх особливостей її графіка.

Провівши попередньо дослідження, ми шукаємо характерні для даного графіка точки і тим спрощуємо розв’язок задачі про по-будову графіка.

При дослідженні функції і побудові її графіка доцільно дотримуватися такої схеми:

Перший етап (використання виду заданої функції).

1). Знаходимо область визначення функції, точки розриву; 2). Досліджуємо функцію на парність чи непарність, періоди-

чність; 3). Знаходимо асимптоти графіка функції;

4). Знаходимо точки перетину графіка функції з осями коор-динат.

Другий етап (використання похідної першого порядку). 5). Знаходимо критичні точки першого роду, інтервали

зростання і спадання, точки екстремумів та екстремальні значення функції.

Третій етап (використання похідної другого порядку).

6). Знаходимо критичні точки другого роду, інтервали опук-лості і вгнутості, точки перегину та значення функції в цих точках.

Четвертий етап. Складемо таблицю результатів дослідження. Наносимо отримані точки, асимптоти на координатну площи-ну і будуємо графік функції з урахуванням точок розриву, інтерва-

лів зростання та спадання функцій, проміжків опуклості та вгнутості графіка функцій.

Приклад 1.Дослідити функціюy=x³−3x²та побудувати їїграфік.

Розв’язування.

1) Область визначення функції : вся числова вісь (−∞,∞) 2). Функція ні парна ні непарна, оскільки

y( − x ) =− x³ − 3 x² ,а тому y( − x ) ≠ y( x ) ≠ − y( x ).

Функція не періодична.

3). Вертикальних асимптот графік немає, бо нема точок роз-

риву.

Дослідимо чи графік має похилі асимптоти y = kx + b :

k = lim y = lim x³ − 3 x² = lim ( x² − 3 x ) =∞ .

x

x→∞ x x→∞ x→∞

Похилих асимптот графік також немає.

4). Знайдемо точки перетину графіка функції з осями коорди-

нат: при x = 0 , y = 0; тобто точка O( 0;0 );

при y = 0 x³ − 3 x² = 0 ⇒ x² ( x − 3 ) = 0 ⇒ x = 0 і x = 3,

тобто точка M ( 3;0 ).

Другий етап.

5). Знаходимо похідну першого порядку: y′= 3 x² − 6 x = 3 x( x − 2 ).

Знаходимо критичні точки першого роду:

3 x( x − 2 ) = 0 , x₁ = 0 , x₂ = 2.

Критичні точки розбивають область визначення на проміжки

(−∞,0)∪(0,2)∪(2,∞) (мал.19).Знаходимо знаки похідної в цих про-міжках:

y′( 3 ) = 3⋅ 3( 3 − 2 ) = 9 > 0, + - +

y′( 1 ) = 3 ⋅ 1( 1 − 2 ) =−3 < 0 , Мал.19

y′( −1 ) = 3( −1 )( −1 − 2 ) = 9 > 0.

Отже, функція зростає на проміжках( −∞ ,0 ) ∪ ( 2;∞ ) , спадає на проміжку ( 0;2 ) .

В точці x = 0 функція має максимум, y_max = y( 0 ) = 0.

В точці x=2 функція має мінімум, y_min = y( 2 ) = 2³ − 3⋅ 2² = 8 − 12 = −4.

Третій етап.

6). Знаходимо похідну другого порядку:

y′′= 6 x − 6 = 6( x − 1 ). Знаходимо критичні точки другого ро-ду: 6( x − 1 ) = 0 ,x = 1. Критична точка x = 1 розбиває область ви-значення на проміжки: ( −∞ ,1 ) ∪ ( 1,∞ ) (мал.20).

Знаходимо знаки другої похідної в цих проміжках:

y′′( 0 ) = 6( 0 − 1 ) =−6 < 0 , - +

y′′( 2 ) = 6( 2 − 1 ) = 6 > 0.

Мал.20

Отже, графік функції опуклий на про-

міжку ( −∞ ;1 ) , вгнутий на проміжку ( 1;∞ ) . Точка x = 1 є точкою

перегину, y_пер_. = y( 1 ) = 1³ − 3 ⋅ 1² = 1 − 3 =−2.

7). Складемо таблицю, де занесемо всі результати дослі-

дження

х (-∞;0) (0;1) (1;2) (2:∞)

у^′ + - - - +

_у′′ - -6 - + +

у -2 -4

макси_мум- ∪

∩ ∩ перегин ∪ мінімум

Знайдемо ще додатково у

y( −1 ) = ( −1 )³ − 3 ⋅ ( −1 )² =−4.

Наносимо всі характерні точки

на координатну площину і буду-

ємо графік (мал.21). -1 О х

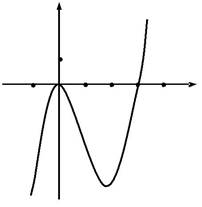
-2

_-4 Мал.21

Приклад 2.Дослідити функціюy= 2 x − 6 та побудувати її

( x − 2 )²

графік.

Розв’язування. Перший етап.

1). Область визначення функції ( −∞ ;2 ) ∪ ( 2;∞ ). Функція має

розрив в точці x = 2.

2). Функція ні парна ні непарна, оскільки

y( − x ) = − 2 x − 6 = − 2 x + 6 і y( − x ) ≠ y( x ) ≠ − y( x ).

( − x − 2 )² ( x + 2 )²

Функція неперіодична.

3) Оскільки в точці розриву x = 2 ,

lim y = lim 2 x − 6 = −∞ , а

x→2−0 x→2−0 _{( x} − _{2 )}²

lim y = lim 2 x − 6 = + , то пряма x = 2 -вертикальна

x→2+0 x→2+0 _{( x} − _{2 )}²

асимптота.

Дослідимо чи графік має похилі асимптоти y = kx + b :

2 x − 2 −

k = lim y = lim = lim x = 0 .

x→∞ x x→∞ _{x( x} − _{2 )}² x→∞ _{( x} − _{2 )}²

b = lim ( y − kx ) = lim 2 x − 6 = 0 .

x→∞ x→∞ ( x − 2 )²

Отже, y = 0 - горизонтальна асимптота.

4). Знайдемо точки перетину графіка функції з осями коорди-

нат: при x = 0 , y = − 6 = − , тобто точка M ₀ ( 0;− ) ;при y = 0 ,

( −2 )²

2 x − 6 = 0 , x = 3, тобто точка M₁ ( 3;0 ).

( x − 2 )²

Переходимо до другого етапу:

5). Знайдемо похідну першого порядку:

y′ = ( 2 x − 6 )′( x − 2 )² − (( x − 2 )² )′( 2 x − 6 ) =

( x − 2 )⁴

= 2( x − 2 )² − 2( x − 2 )( 2 x − 6 ) = 2( x − 2 ) − 2( 2 x − 6 ) =

( x − 2 )⁴ ( x − 2 )³

= 2 x − 4 − 4 x + 12 = 8 − 2 x .

( x − 2 )³ ( x − 2 )³

Знаходимо критичні точки першого роду:

8 − 2 x

= 0 ;8 − 2 x = 0 ; x = 4. - + -

( x − 2 )³

4 Мал.22

Враховуючи точку x=2, де похі-

дна не існує, розіб’ємо область визна-

чення на проміжки ( −∞ ,2 ) ∪ ( 2;4 ) ∪ ( 4;8 ) (мал.22) і встановимо

знаки першої похідної в цих проміжках:

y′( 1 ) = 8 − 2 = =−6 < 0 ;

( 1 − 2 )³

− 1

y′( 3 ) = 8 − 2 ⋅ 3 > 0; y′( 5 ) = 8 − 2 ⋅ 5 = − < 0.

( 3 − 2 )³ ( 5 − 2 )³

Отже, функція зростає на проміжку ( 2;4 ) , спадає на проміж-

ках ( −∞ ;2 ) ∪ ( 4;∞ ). В точці x = 4 функція має максимум,

y_max = y( 4 ) = 2 ⋅ 4 − 6 = = . Маємо точку M₂( 4; ).

( 4 − 2 )²

Переходимо до третього етапу:

6). Знаходимо другу похідну:

y′′= ( 8 − 2 x )′( x − 2 )³ − (( x − 2 )³ )′( 8 − 2 x ) =

( x − 2 )⁶

= − 2( x − 2 )³ − 3( x − 2 )² ( 8 − 2 x ) = − 2( x − 2 ) − 3( 8 − 2 x ) =

( x − 2 )⁶ ( x − 2 )⁴

₌− 2 x + 4 − 24 + 6 x = 4 x − 20 .

( x − 2 )⁴

( x − 2 )⁴ - - +

Знайдемо критичні точки другого роду:

4 x − 20 Мал.23

= 0; 4 x − 20 = 0; x = 5.

( x − 2 )⁴

Враховуючи точку x = 2 ,де y′′ не існує, розбиваємо область ви-

значення на проміжки: ( −∞ ;2 ) ∪ ( 2;5 ) ∪ ( 5;∞ ) (мал.23).

Встановимо знаки другої похідної в цих проміжках:

y′′( 0 ) = − 20 = − = − < 0 , y′′( 3 ) = 4 ⋅ 3 − 20 = − =−8 < 0 ,

( 3 − 2 )⁴

( −2 )⁴

y′′( 6 ) = 4 ⋅ 6 − 20 = = > 0.

( 6 − 2 )⁴

4⁴

Отже, графік функції опуклий на проміжках: ( −∞ ;2 ) ∪ ( 2;5 ) , вгну-тий на проміжку ( 5;∞ ). Точка x = 5 є точкою перегину,

y = y(5 ) = 2⋅ 5 − 6 = . Маємо точку M ( 5; ).

(5 − 2 )²

пер.

7). Складемо таблицю, де занесемо результати дослідження

(-∞;0) (0;2) (2;3) (3;4) (4;5) (5:∞)

у ′ - - - не + + + - - -

існує

у^′ - - - не - - - - - +

′ існує

у не 0,5 4

∩ − ∩ існує ∩ ∩ ∩ ∪

-

висновок Функція точка Функція вертикальнаасимптота Фунція точка Функція Точка перегину Функція максимум Функція

Спадає , перетину спадає, Зростає, перетину зростає, спадає спадає,

Графік з віссю графік Графік з віссю графік графік графік

Опук- Оу опуклий Опуклий Ох опуклий опуклий опуклий

лий

Будуємо графік (мал.24).

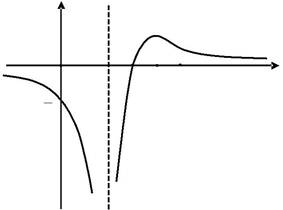
у

О 23 4 5 х

− ₂³

Мал.24

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Асимптоти графіка функції	\|	Еластичність функції

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.015 сек.