• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Інтеграла дорівнює підінтегральній функції.

Отже похідна від первісної дорівнює підінтегральній функції.

ТЕОРЕМА 4.(Властивість2)Диференціал від невизначе-

Ного інтеграла дорівнює підінтегральному виразу

d (_∫ f ( x )dx)= f ( x )dx (6.5)

Доведення.За означенням диференціалаd ( f ( x ))=f′( x )dx.

Тому

d (_∫ f ( x )dx)= d( F ( x ) + C )= d( F ( x ))= F ′( x )dx = f ( x )dx .

ТЕОРЕМА 5.(Властивість3)Невизначений інтеграл від

диференціала деякої функції F(x) дорівнює цій функції з точністю до довільної сталої,

Доведення.Продиференціюємо ліву і праву частини рівності.

Одержимо: d _∫d ( F ( x )) = d ( F ( x )) = f ( x )dx і

d( F( x ) + С ) = d( F( x )) = F′( x )dx = f ( x )dx .

Праві частини рівностей однакові. Значить рівні й ліві. Теоре-му доведено.

Аналогічно, диференціюванням лівої і правої частин рівності, доводяться теореми 6 і 7.

ТЕОРЕМА 6.(Властивість4).Сталий множник можна ви-

Носити за знак невизначеного інтеграла.

ТЕОРЕМА 7.(Властивість5)Інтеграл від алгебраїчної су-

Ми скінченого числа функцій дорівнює алгебраїчній сумі інтегралів від цих функцій

Таблиця невизначених інтегралів

Інтегрування є операція, обернена до диференціювання. Тому формули інтегрування отримують з формул для знаходження похід-них. А універсальність застосування формул інтегрування випливає з теореми про незалежність вигляду невизначеного інтеграла від вибору аргументу (інваріантність невизначеного інтеграла відносно змінної інтегрування ).

ТЕОРЕМА 8. Нехай f(x) – деяка неперервна функція на даному проміжку, х – незалежна змінна, F(x) – її первісна,

_∫ f ( x )dx = F( x ) + C і нехай u =ϕ( x ) неперервно диференційо-

вана функція. Тоді_∫f ( u )du=F ( u )+C . (6.9)

Доведення.Розглянемо інтеграл_∫f ( u )du=_∫f ( u )u′dx.Вцьому випадку складна функція F( u ) = F( ϕ( x )) є первісна для f(u).

Справді, внаслідок незалежності диференціала першого по-рядку від вибору незалежної змінної, одержуємо dF ( u ) = F ′( u )du = f ( u )du .При цьому

Тому, з справедливості формули (6.3), випливає справедли-вість формули

Отже формулами інтегрування можна користуватись при будь-якій змінній інтегрування. Використовуючи таблицю дифере-нціалів основних елементарних функцій, виведемо деякі формули інтегрування. Інші виводяться аналогічно.

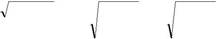
₅₎ ∫_uⁿ_{du =} ^{un+ 1} _{+ C , ( n ≠ −1 ) .} n + 1

Для виведення цієї формули використовують формулу для знаходження диференціала duⁿ = nu^{n− 1}du . Якщо показник степеня дорівнює n+1 формула запишеться так: du^{n+ 1} = ( n + 1 )uⁿdu .

Інтегруючи цю формулу (ліву і праву частину) і, зробивши перетво-рення, одержимо

доводяться диференціюванням лівої і правої частин рівності. Такий метод доведення формул можна використовувати для

будь-якої формули інтегрування.

7) Доведемо справедливість формули _∫ ¹_хdx = lnх + C .

Для компактності всі формули зводять в таблицю.

Читайте також:

1. Банківська система: сутність, принципи побудови та функції. особливості побудови банківської системи в Україн
2. Банківська система: сутність, принципи побудови та функції. Особливості побудови банківської системи в Україні.
3. Банківська система: сутність, принципи побудови та функції. Особливості побудови банківської системи в Україні.
4. Бульові функції.
5. Вартість робочої сили. Заробітна плата, її форми і функції.
6. Види речень в ділових паперах та їх стилістичні функції.
7. Види речень в ділових паперах та їх стилістичні функції.
8. Виписати проміжки монотонності функції.
9. Вказівники на функції. Масиви вказівників на функції
10. Властивості визначеного інтеграла
11. Геометричний зміст визначеного інтеграла.
12. Геометричні застосування визначеного інтеграла.

Переглядів: 999