• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Поверхні переносу

Поверхні, утворені поступальним рухом твірної за заданою траєкторією, називають поверхнями переносу. Серед значної кількості таких поверхонь найбільш розповсюджені в інженерній практиці:

1. Лінійчаті поверхні з двома напрямними та площиною паралелізму, або так звані поверхні Каталана (Каталан Е. – бельгійський математик, який досліджував властивості цих поверхонь). В групу поверхонь Каталана, показаних на рис.5.6, входять гіперболічний параболоїд, коноїд, циліндроїд. Всі перелічені поверхні утворюються внаслідок поступального руху прямої лінії, яка по всіх своїх положеннях перетинає дві напрямні лінії m і n залишаючись паралельною площині α, що і отримала назву „площина паралелізму”. У гіперболічного параболоїда напрямні лінії – дві мимобіжні прямі (див.рис.5.6 а), у коноїда – одна напрямна пряма, інша крива (див. рис.5.6,б), у циліндроїда напрямні лінії – криві (див. рис.5.6,в)

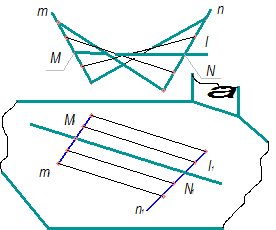
а) б)

в)

Рисунок 5. 6 - Поверхні Каталана

Окремим випадком гіперболічного параболоїда є площина, яка утворюється, коли напрямні лінії m і n перетинаються або паралельні між собою. Перелічені поверхні з площиною паралелізму є різновидом поверхонь з напрямною площиною. Тому визначник таких поверхонь буде мати вигляд:

Defθ = (ℓ, m, n, α) [A],

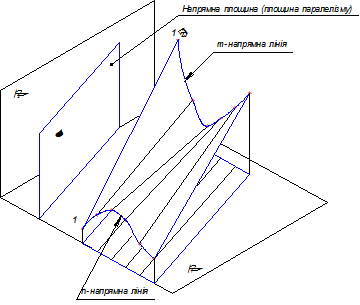де [A] – алгоритмічна частина , що містить в собі характеристику руху прямолінійної твірної ℓ, яка при всіх положеннях зберігає постійний кут φ ( для циліндроїда, коноїда та гіперболічного параболоїда кут складає 0˚) відносно напрямної площини α. Поверхні Каталана на прямокутних проекціях задають у вигляді відповідних проекцій каркасу – сукупності твірних.

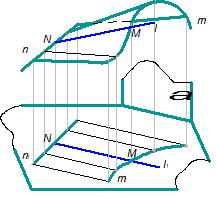
Утворення прямокутних проекцій циліндроїда коли напрямною площиною є площина окремого положення Σ, а напрямні лінії є плоскі криві mі n, показано на рис. 5.7.

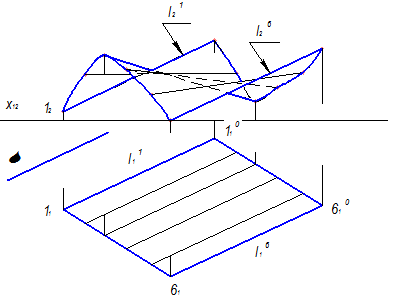
Рисунок 5.7 - Утворення прямокутних проекцій циліндроїда

Послідовність побудови проекцій лінійного каркаса поверхні Каталана (коноїда) за заданими проекціями напрямних ліній m (m1, m2) і n (n1,n2) та площини паралелізму α (α2) наведено нижче:

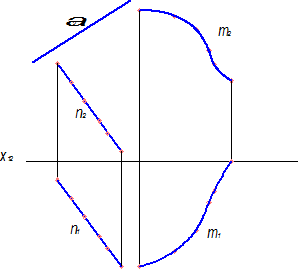
1. За умови площина паралелізму α (α2) займає фронтально-проекціювальне положення. Тому фронтальну проекцію першої лінії каркаса ℓ2 (1222) будуємо паралельно відповідній фронтальній проекції площини паралелізму α (α2). Горизонтальну проекцію лінії ℓ визначаємо шляхом побудови горизонтальних проекцій точок 1 і 2, які належать напрямним прямим m і n:

2. Наступну лінію каркаса будуємо аналогічно: починаємо з проведення

її фронтальної проекції (32,42), паралельно проекції площини паралелізму α (α2), а потім визначаємо за лініями зв’язку її горизонтальну проекцію (31,41):

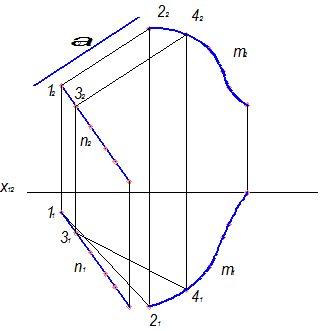
3. Будуємо необхідну за щільністю множину ліній каркаса.

4. Для наочності виділяємо першу і останню лінії каркаса суцільними основними товстими лініями креслення. Визначаємо видимість ліній каркаса відносно площин проекцій шляхом використання штрихових ліній креслення:

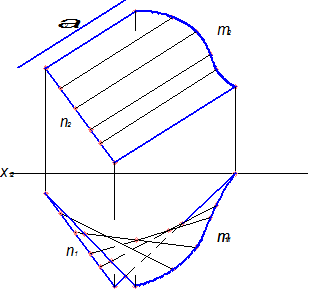
2. Лінійчаті поверхні з однією напрямною (торси). В групу входять поверхні з ребром звороту, циліндрична поверхня, конічна поверхня. Торсом називають поверхню, над якою можна здійснити процес суміщення всіма її точками з площиною без складок та розривів. Такі поверхні ще називають розгортними поверхнями. Характерною ознакою розгортних поверхонь є те, що їх прямолінійні твірні перетинаються. Розгортну лінійчату поверхню можна уявити собі як граничний стан гранної поверхні з гранями, ширина яких наближається до нуля. Тому така поверхня може бути, як багатогранник, розгорнута на площину. В загальному вигляді розгортна поверхня утворюється як неперервна множина дотичних {ℓі } до просторової кривої лінії a і називається торсом (рис. 5.8).

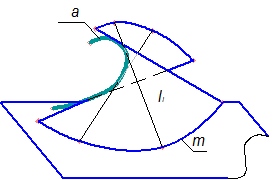
Рисунок 5.8 - Формоутворення торсової поверхні загального виду

Криву a називають ребром звороту торса.

Найпростішими окремими випадками торса є конічна і циліндрична поверхні, у яких ребро звороту стягується в точку. У конічної поверхні, яка показана на рис.5.9,а, це точка S – його вершина, у циліндричної поверхні (див. рис.5.9,б – нескінченно віддалена точка перетину прямолінійних твірних S∞.

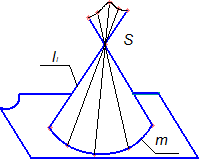
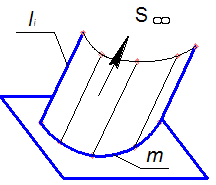
а) б)

Рисунок 5.9 - Окремі випадки торсових поверхонь

Плоску криву m (див. рис5.8 та рис.5.9), яка утворюється внаслідок перерізу торсових поверхонь площиною, називають напрямною лінією.

Визначник цієї групи поверхонь має вигляд:

Defθ = (ℓ, а) [A],

де [A] – алгоритмічна частина, яка містить умову, що твірна ℓ при русі торкається ребра звороту а, або його перетворень у вигляді точок S та S∞.

Для задання торсової поверхні загального вигляду на прямокутних проекціях достатньо задати відповідні проекції її визначника - ребра звороту n (n1,n2) та побудувати сукупність прямокутних проекцій прямих, що утворюють лінійчатий каркас поверхні, показаної на рис. 5.10.

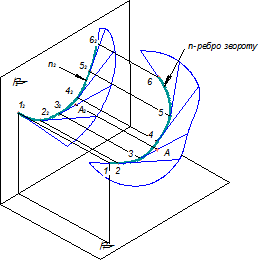
Рисунок 5.10 -Утворення прямокутних проекцій торсової поверхні загального вигляду

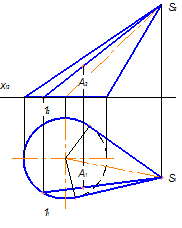
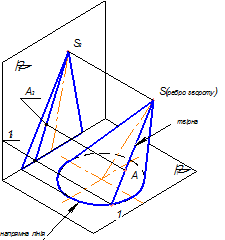
Рисунок 5.11 - Утворення прямокутних проекцій еліптичного конуса

Якщо напрямну лінію m прийняти замкнуту плоску криву, то тіло, обмежене циліндричною поверхнею, має назву циліндра, який показано на рис. 5.12.

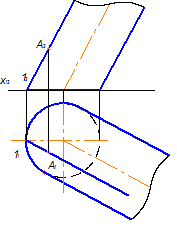
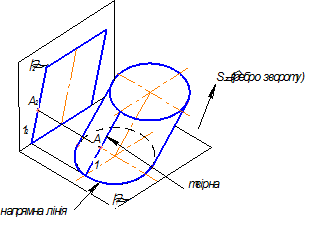
Рисунок 5.12 - Утворення прямокутних проекцій еліптичного циліндра

3. Поверхні паралельного переміщення. В групу таких поверхонь входять поверхні, що утворюються внаслідок поступального руху твірної лінії ℓ, одна з точок якої переміщується вздовж напрямної лінії m, а всі інші здійснюють паралельне переміщення. Визначник поверхонь паралельного переміщення, яка показана на рис. 5.13, має вигляд:

Defθ = (ℓ, m) [A],

де [A] – алгоритмічна частина, яка складається з умови паралельного переміщення точок твірноїℓ .

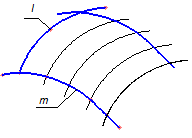
Рисунок 5.13 - Формоутворення поверхні паралельного переміщення

На прямокутних проекціях поверхні паралельного переміщення задають у вигляді проекцій їх визначника: сукупності відповідних проекцій напрямної лінії та твірних ліній. На рис. 5.14 показана поверхня паралельного переміщення, утворена незамкненою кривою лінією ℓ.

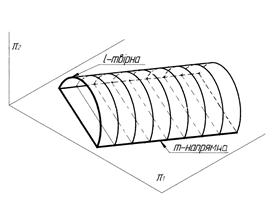
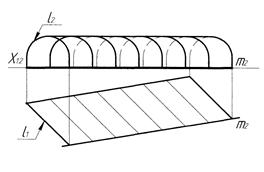
Рисунок 5.14 - Утворення прямокутних проекцій поверхні паралельного переміщення

Поверхня паралельного переміщення може бути утворена замкненою кривою лінією. Такі поверхні, приклад якої показано на рис.5.14, відносять до каналових поверхонь.

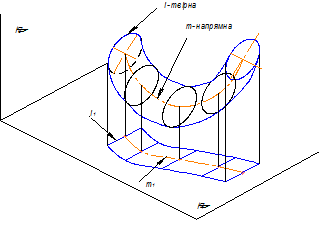
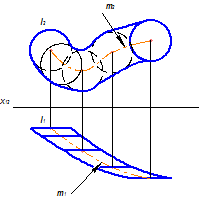
Рисунок 5.15 - Утворення прямокутних проекцій поверхні паралельного переміщення з замкненою твірною лінією

Читайте також:

1. Алгоритм розрахунку температури поверхні чипу ІМС процесора
2. Великої питомої поверхні пилинок (відношення площі поверхні до їх
3. Визначення температури на поверхні ізоляції принадземномупрокладанні та при прокладанні трубопроводів в приміщенні.
4. Визначення числа одиниць переносу
5. Вимірювання розмірів деталей та шорсткуватості поверхні
6. Вплив рослин та тваринних організмів на процеси переносу
7. Джерело шуму , розташовують у кожусі, внутрішні поверхні якого покривають звукопоглинальними матеріалами. Різновидом цього методу є кабіна керування.
8. Еджескопія – відділ дактелоскопії , за яким здійсн криміналістичне дослідження нерівностей будови країв попелярних ліній на долонях поверхні рук і підошв ніг.
9. Еквіпотенціальні поверхні. Зв’язок напруженості поля та потенціалу.
10. Електроліз – сукупність окисно-відновних процесів, що протікають на поверхні електродів при проходженні постійного електричного струму через розплав чи розчин електроліту.
11. Забруднення земної поверхні відвалами шлаків і кар’єрами.
12. Загальні риси будови поверхні

Переглядів: 1793