• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Об’єднання компонентів. Модель середовища

Для визначення семантики об’єднання компонентів за графом G, використовуються мова IDL для опису параметрів типу In, Out і Inout операцій приналежності:

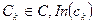– множина вхідних (In) інтерфейсних компонентів;

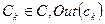– множина вихідних (Out) інтерфейсних компонентів.

Результатом об’єднання двох компонентів буде компонент, у якого множина вхідних інтерфейсів співпадає з множиною вхідних інтерфейсів компонента-приймальника, а множина вихідних інтерфейсів – з множиною вихідних інтерфейсів компонента-передавача:

, , .

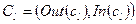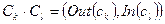Аксіома. Композиціякомпонентів 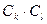є коректною, якщо компонент-передавач C_k повністю забезпечує сервіс, необхідний компоненту-приймальнику C_i, тобто

.

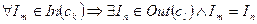Компонентні ПС можуть мати декілька інтерфейсів і успадковувати інтерфейси інших компонентів ( 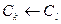), тоді останні надають сервіс всієї множини вихідних інтерфейсів: .

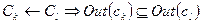У випадку, коли компонент успадковує інший компонент, у якого множина вихідних інтерфейсів містить всі його інтерфейси, а множина вхідних інтерфейсів містить тільки інтерфейси, необхідні для надання сервісу, то маємо

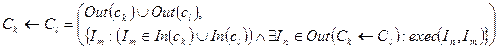
Успадкований компонент делегує усі інтерфейси і має властивості:

транзитивності ;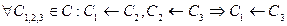

симетричності .

Ці властивості компонентів ідентичні компонентам моделі ПС. Для їх розміщення у деякому середовищі необхідно виконати такі дії:

– визначити критерії й умови розташування компонентів у вузлах середовища з урахуванням зв'язків між ними відповідно компонентного графу;

– визначити засоби передачі повідомлень від одного компонента до іншого;

– об'єднати програмні компоненти і їхні інтерфейси у структуру ПС з КПВ .

Таким чином, виходячи з запропонованої моделі СМ, моделі взаємодії [17] та семантики її виконання, компоненти цієї моделі ПС, можуть бути розподілені по вузлах мережі і взаємодіяти між собою через механізми інтерфейсів і повідомлень.

Модель компонентного середовища. Ця модель має наступний вигляд:

CE = (CNa, InRep, ImRep, CSe, CSeIm), (7)

де CNa = {CNa^m} – множина імен компонентів, які входять до складу середовища, InRep = {InRepⁱ} – репозитарій інтерфейсів компонентів середовища, ImRep = {ImRep^j} – репозитарій реалізацій, CSe = {CSe^r} – інтерфейс системних сервісів, CSeIm = {CSeIm^r} – множина реалізацій для системних сервісів.

Кожен елемент з InRep описується двійкою (CInⁱ, CNa^m), де CInⁱ – інтерфейс компонента, який описується виразом (4), а CNa^m – ім’я компонента, що реалізує інтерфейс. Аналогічно кожен елемент з ImRep описується (CIm^j, CNa^m), де CIm^j – реалізація, яка описується виразом (5), а CNa^m – ім’я компонента, до якого належить ця реалізація.

Компонентне середовище розглядається як множина серверів застосувань, де розгортаються компоненти-контейнери, екземпляри яких забезпечують реалізацію функціональності компонента. Взаємозв’язок контейнера з сервером забезпечується через стандартизовані інтерфейси (CFa). Зв’язок між компонентами, які розгорнуті у різних серверах забезпечується реалізаціями інтерфейсу.

Означення 1. Каркасом компонентного середовища називається середовище, для якого CNa, InRep, ImRep – суть порожні множини, тобто

FW = (Æ, Æ, Æ, CSe, CSeIm). (7)

Нехай FW₁= (Æ, Æ, Æ, CSe₁, CSeIm₁) і FW₂ = (Æ, Æ, Æ, CSe₂, CSeIm₂) – два каркаси.

Означення 2. Каркас FW₁ сумісний з каркасом FW₂, якщо існує відображення SMap: CSe₁ –> CSe₂ таке, що SMap(CSe₁) Í CSe₂.

Компонентна алгебравключає зовнішню алгебру на верхньому рівні моделі щодо ПС і внутрішню алгебру щодо внутрішній структури КПВ.

å = {Y Ç j } = {CSet, CESet, W₁} Ç {CSet, CESet, W₂}, (8)

де Y – зовнішня алгебра, j – внутрішня алгебра.

Зовнішня компонентна алгебра визначає множину операцій над множинами компонентів компонентних середовищ і описується наступним виразом

Y = { CSet, CESet, W₁},

де CSet – множина компонентів C, , кожен з яких описується виразом (3),

CESet – множина компонентних середовищ, кожне з яких описується виразом (7),

W₁= {CE₁, CE₂, CE₃, CE₄} – операції зовнішній алгебри, а саме такі:

CE₁ – операція оброблення компонентів,

CE₂ = C Å CE₁ – операція інсталяції,

CE₃ = CE₁ Ç CE₂ – операція зборки (об’єднання) середовищ,

CE₄ = CE₁ \ C.– операція видалення компонента С з середовища,

C₂ – CE₂ = C₂ Å (CE₁ \ C₁) – операція заміщення.

Для операцій зовнішній алгебри доведені наступні теореми.

Теорема 2. Кожне компонентне середовище CE є результатом виконання послідовності операцій розгортання компонентів, які входять до його складу, у певному компонентному каркасі: CE = C₁ Å C₂ Å . . . Å C_n Å FW.

Теорема 3. Побудова компонентного середовища не залежить від порядку інсталяції компонентів, які входять до складу цього середовища, тобто:

C₁ Å (C₂ Å CE) = C₂ Å (C₁ Å CE).

Теорема 4. Операція об'єднання компонентних середовищ асоціативна:

(CE₁ È CE₂) È CE₃ = CE₁ È (CE₂ È CE₃).

Теорема 5. Операція об'єднання компонентних середовищ комутативна:

CE₁ È CE₂ = CE₂ È CE₁.

Теорема 6. Для будь-якого компонентного середовища

CE È FW = FW È CE = CE.

Теорема 7. Для довільних компонентних середовищ CE₁ і CE₂ та компонента C завжди виконується:

C Å (CE₁ È CE₂) = (C Å CE₁) È CE₂ = (C Å CE₂) È CE₁.

Теорема 8.. Для будь-якого компонента C та компонентного середовища CE завжди виконується: (C Å CE) \ C = CE.

Читайте також:

1. G2G-модель електронного уряду
2. OSI - Базова Еталонна модель взаємодії відкритих систем
3. А. Заходи, які направлені на охорону навколишнього середовища та здоров’я населення.
4. Абстрактна модель
5. Абстрактна модель
6. Абстрактна модель оптимального планування виробництва
7. Адаптація до абіотичних факторів середовища.
8. Адаптація організму до змін чинників зовнішнього середовища
9. Адаптація організму до зовнішніх факторів середовища.
10. Американська модель соціальної відповідальності
11. Аналіз внутрішнього середовища підприємства
12. Аналіз зовнішнього середовища

Переглядів: 657