
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Семантичні аспекти взаємодії різнорідних програм
Проблема взаємодії з семантичної точки зору – це забезпечення сумісності типів даних за допомогою операцій перетворення форм представлення типів даних у програмах МП до релевантного або єдиного програмного коду середовища у випадку деяких відмінностей в описі типу змінної в операторах виклику програм одна одною. Крім того, базовий тип даних у різних МП може бути неадекватно реалізований відповідними системами програмування та зв'язаними з ними платформами. На формальному рівні мова йде про ізоморфне перетворення типів даних до вигляду, що підходить для компонента, що викликається, і середовища виконання.
Випадки ізоморфного перетворення типів даних.
1. Ізоморфізм між множинами значень типів даних МП і множиною операцій існує.
2. Ізоморфізм між множинами значень типів даних МП і різними операціями існує при деяких обмеженнях.
3. Ізоморфне відображення між множинами значень типів даних різних МП не існує.
Ізоморфізм відображень множини значень t типів даних T за допомогою операцій 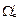 визначається потужністю системи перетворення, під якою розуміється потужність множини
визначається потужністю системи перетворення, під якою розуміється потужність множини  [6]. Даний тривіальний результат може служити вагомим критерієм оцінки правильності взаємодії програм для випадку, якщо в різних МП однакові типи даних мають різні множини значень. Іншим застосуванням цього критерію може служити перенос програмних систем з різномовних компонентів з комп'ютера одного типу на комп'ютер іншого типу, причому ці типи мають різні архітектури та діапазони цілих і дійсних чисел.
[6]. Даний тривіальний результат може служити вагомим критерієм оцінки правильності взаємодії програм для випадку, якщо в різних МП однакові типи даних мають різні множини значень. Іншим застосуванням цього критерію може служити перенос програмних систем з різномовних компонентів з комп'ютера одного типу на комп'ютер іншого типу, причому ці типи мають різні архітектури та діапазони цілих і дійсних чисел.
Аналізуючи множини операцій 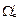 , можна відзначити, що вони усі містять операції співставлення. Тому на самих множинах
, можна відзначити, що вони усі містять операції співставлення. Тому на самих множинах  задане відношення порядку. З огляду на те, що будь-які два елементи з
задане відношення порядку. З огляду на те, що будь-які два елементи з  порівнянні, це відношення визначає лінійний порядок. У цьому випадку ізоморфне відображення повинне зберігати відношення лінійного порядку.
порівнянні, це відношення визначає лінійний порядок. У цьому випадку ізоморфне відображення повинне зберігати відношення лінійного порядку.
Нехай ∑ – множина алгебраїчних систем, побудованих вище. Тоді має місце наступна лема.
Лема. Для будь-якого ізоморфного відображення φ між системами відображень виконуються рівності
φ(  ) =
) =  , φ(
, φ( 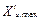 ) =
) = 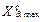 .
.
Доказ даної леми простий. Для всіх побудованих систем перетворення, що описують прості типи даних, множини значень обмежені. Відповідно до аксіоми, мінімальні і максимальні елементи цих множин їм належать. Структурні типи цих даних будуються з простих за допомогою кінцевого числа операцій, а їх множини значень також кінцеві. Тому  ,
, 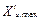 ,
,  ,
, 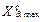 існують і належать до множин
існують і належать до множин  та
та 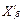 відповідно. З огляду на лінійну впорядкованість цих множин, необхідно щоб виконувалася умова леми. Якщо б воно не виконувалося, то ізоморфне відображення не зберігало б лінійний порядок, що суперечить зробленому раніше висновку. Лема доведена.
відповідно. З огляду на лінійну впорядкованість цих множин, необхідно щоб виконувалася умова леми. Якщо б воно не виконувалося, то ізоморфне відображення не зберігало б лінійний порядок, що суперечить зробленому раніше висновку. Лема доведена.
Системи ізоморфного відображення між основними типами даних (перелічуваний тип – у перелічуваний; булевий – у булевий; цілий – у цілий; дійсний – у дійсний) розглядати не будемо в силу їхньої простоти. Однак можливі більш складні перетворення між наступними типами даних: символьний – у цілий; символьний – у булевий; цілий – у символьний; цілий – у булевий; булевий – у цілий; булевий – у символьний. Ці види семантичного перетворення представлені та їм даний доказ у [ 6].
При виконанні операцій перетворення масивів і записів повинен зберігатися тільки лінійний порядок. Можливі наступні види перетворень: масив – у масив, запис – у запис, масив – у запис, запис – у масив.
Розглянемо, наприклад, перше з них. Нехай φ – їх ізоморфізм, що зберігає лінійний порядок. Це означає, що
( 
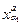
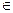
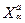 ) & (
) & ( 
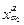
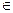
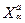 )& (
)& ( 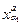 ≤
≤ 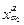 )
) 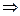 φ(
φ( 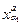 )≤ φ(
)≤ φ( 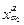 )
)
Тут 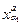 і
і 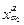 – функції відображення. Виконання відношення ≤ для функцій означає виконання цього відношення для всіх елементів області визначення цих функцій. З вираження для функцій φ(
– функції відображення. Виконання відношення ≤ для функцій означає виконання цього відношення для всіх елементів області визначення цих функцій. З вираження для функцій φ( 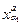 ) і φ(
) і φ( 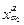 ) випливає:
) випливає:
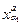 :
: 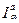 → Y(
→ Y( 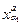 ), Y(
), Y( 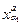 )
) 
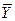 (
( 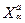 ),
),
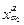 :
: 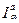 → Y(
→ Y( 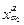 ), Y(
), Y( 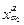 )
) 
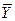 (
( 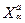 ).
).
Нехай виконується відображення:
φi : 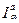 →
→  , φy :
, φy : 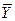 (
( 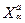 ) →
) → 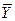 (
( 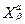 )
)
де φi і φy – ізоморфні відображення, що відповідають множинам індексів i та значенням y для елементів масиву. Через Е1позначимо вкладення Y( 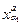 )→
)→ 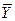 (
( 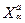 ), а через Е2– вкладення Y(
), а через Е2– вкладення Y( 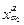 ) →
) → 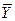 (
( 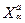 ). Тоді φ(
). Тоді φ( 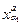 )і φ(
)і φ( 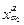 ) будуть визначатися як обмеження відображення φу на відповідні підмножини та позначатися через φу|Y(
) будуть визначатися як обмеження відображення φу на відповідні підмножини та позначатися через φу|Y( 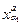 )і φу|Y(
)і φу|Y( 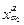 ) відповідно. Остання нерівність буде еквівалентноюφу | Y(
) відповідно. Остання нерівність буде еквівалентноюφу | Y( 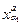 ) ≤ φ у | Y(
) ≤ φ у | Y( 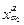 ).
).
Розглянемо далі перетворення типу запис – в інший запис. У теорії структурної організації даних множина значень записів визначається як прямий добуток множини значень їх окремих елементів. Даний підхід до опису записів представлений на прикладі множини значень для трьох описів елементів запису а), б), в):
а) tуре 
 = (
= (  :
: 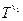 ;
;  :
: 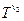 ;
; 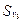 :
: 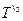 ),
),
б) type 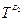 = (
= ( 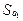 :
: 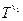 ; S':T'), type T' = (
; S':T'), type T' = (  :
: 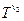 ;
; 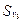 :
: 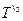 ),
),
в) type 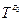 = (S':T';
= (S':T'; 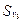 :
: 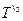 ), type T' = (
), type T' = (  :
: 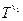 ;
;  :
: 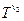 ).
).
Описи трьох типів записів  ,
, 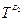 ,
, 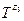 відрізняються, їх множини значень збігаються в плані завдання перетворення їхніх типів даних. Між множинами типів даних записів можливо встановити взаємно однозначну відповідність за двох умов:
відрізняються, їх множини значень збігаються в плані завдання перетворення їхніх типів даних. Між множинами типів даних записів можливо встановити взаємно однозначну відповідність за двох умов:
– кількість компонентів у записах однакова;
– для кожного з елементів першого запису існує тільки один відповідний елемент другого запису.
Операції співставлення над записами виконуються з урахуванням обраної відповідності, і перетворення запису зводиться до відображення типів окремих елементів. Якщо ізоморфні відображення між окремими елементами дотримуються лінійного порядку, то перетворення ізоморфне.
Нарешті, перетворення «запис – у масив» вимагає, щоб типи всіх елементів запису були однакового типу, а сам запис був представлений у вигляді масиву. Множина значень елементів запису утворить множину значень елементів масиву Y. Множина індексів перевпорядковує компоненти запису: i-й компонент запису ставиться у відповідність φ(i)–му елементові в множині J (φ – взаємо–однозначне відображення). Сама множина I ємножиною значень перелічуваного типу.
Читайте також:
- Cisco Packet Tracer - Знайомство з програмою. Інтерфейс
- I. Введення в розробку програмного забезпечення
- II. Вимоги до складання паспорта бюджетної програми
- II. Із програм для 11 класу
- II. ПРОГРАМА КУРСУ
- II.1 Програмне забезпечення
- III. Етапи розробки програмного забезпечення
- III. Навчально-програмний етап.
- III. Програма
- III. Програма
- OSI - Базова Еталонна модель взаємодії відкритих систем
- WEB ПРОГРАММИРОВАНИЕ
| <== попередня сторінка | | | наступна сторінка ==> |
| Аксіоматика структурних і складних типів даних. Структурні типи даних. | | | Характеристика типів даних для зборки програм |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |