• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Просте нарахування, яке має цілу кількість періодів нарахування процентів.

Для розуміння і засвоєння механізму простого нарахування процентів (англ. simple interest) проаналізуємо й розв’яжемо Модельну задачу 1 (умова ─ жирним шрифтом, пояснення до задачі ─ звичайним).

Ви вклали в комерційний банк 1000 грн. на строк 4 роки під 10% річних на умові щорічного простого нарахування процентів.

Це означає, що наприкінці кожного року Ви одержите в банку процент, рівний 100 грн (1000 грн помножені на 0,1) Цей процент Ви зобов’язані забрати з банку. Наприкінці четвертого року Вам повернуть 1000 грн, вкладені на початку першого року. Внесок грошей у банк називається депозитний вклад (внесок).Потрібно знайти фактичну загальну суму грошей, що Ви одержите по закінченні чотирьох років.

Розв’язання Модельної задачі 1 включає розглядфінансової операції по періодах нарахування процентів.

В умові задачі період нарахування процентів ─ рік.

ПЕРІОД 1 (перший рік): на початку першого року Ви поклали на депозит 1000 грн; наприкінці першого року Ви маєте на депозитному рахунку 1100 грн:

─ розрахунок в періоді 1: 1000 грн + 1000 грн 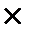0,1 = = 1000 грн (1+0,1) =1100 грн.

В періоді 1 дія: 1000 грн 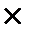0,1 = 100 грн. ─ це розрахунок Вашого процента за перший рік, який Ви одержуєте в банку на руки. Тому на початок другого року у Вас на депозитному рахунку залишається 1000 грн.

ПЕРІОД 2 (другий рік): наприкінці другого року Ви маєте на депозитному рахунку 1100 грн:

─ розрахунок періоду 2: 1000 грн + 1000 грн 0,1 = = 1000 грн 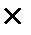(1+0,1) = 1100 грн.

100 грн ─ Ваш процент за другий рік, який Ви забираєте з банку. На початок наступного третього року у Вас на депозитному рахунку залишаються вкладені Вами на депозит 1000 грн.

ПЕРІОД 3 (третій рік): наприкінці третього року Ви маєте на депозитному рахунку 1100 грн:

─ розрахунок періоду 3: 1000 грн + 1000 грн 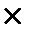0,1 = = 1000 грн 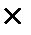(1+0,1) = 1100 грн.

В кінці третього року сума 100 грн ─ Ваш процент за третій рік, який Ви одержуєте в банку на руки. На початок четвертого року у Вас на депозитному рахунку залишаються все ті ж 1000 грн.

ПЕРІОД 4 (четвертий рік): наприкінці четвертого року Ви маєте на депозитному рахунку 1100 грн:

─ розрахунок періоду 4: 1000 грн + 1000 грн 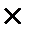0,1 = = 1000 грн (1+0,1) = 1100 грн.

В кінці четвертого року Ви одержуєте з банку на руки 1100 грн, які складаються з 1000 грн, вкладених Вами на початку першого року й 100 грн ─ процент за четвертий період нарахування процентів.

Отже, на початку першого року Ви вклали 1000 грн, а по закінченні чотирьох років Ви одержали фактично 1400 грн, тобто Вам повернули вкладені Вами 1000 грн і нарахували та віддали Вам в кожному із чотирьох років проценти по 100 грн, що в сумі склало 400 грн процентів.

Базою для розрахунку процентів при механізмі простого нарахування процентів є сума вкладу (внеску), що є сумою на початку фінансової операції (PV). МЕХАНІЗМ ПРОСТОГО НАРАХУВАННЯ ПРОЦЕНТІВ МАЄ ЗА УМОВУ НЕЗМІННІСТЬ БАЗИ (БАЗА ─ PV), ВІД ЯКОЇ ЙДЕ НАРАХУВАННЯ.

У фінансах вираз «механізм простого нарахування процентів» може мати декілька виразів-синонімів: «нарощення по простій процентній ставці», «нарахування простих процентів», «проста нарощена вартість», «прості проценти», «проста позика», будь-які інші.

Під простим процентом розуміємо операцію нарахування процентів на теперішню вартість (вкладу, позики, тощо) в кінці кожного періоду нарахування процентів. Період нарахування процентів зазначається умовами фінансової операції (може бути ─ місяць, квартал, рік, тощо).

_____НЕОГОЛОШЕНЕ ПРАВИЛО_(повторно)___

ЯКЩО НЕ ЗАЗНАЧЕНО тривалість періоду нарахування процентів, то ПЕРІОД НАРАХУВАННЯ ПРОЦЕНТІВ ─ ОДИН РІК.

У Модельній задачі 1вкладені Вами в банк на депозит 1000 грн ─ це PV,отримані Вами фактично 1400 грн ─ це FV,процентна ставка дорівнює 10% річних – це i. Крім цих, відомих раніше (див. підрозділ 2.1) показників, які позначені символами PV, FV, i, з’являється показник, що показує, скільки разів впродовж строку фінансової операції нараховувалися проценти. Про нього вже йшла мова в підрозділі 1.6 і цей показник зазначили символом n.

Оскільки прості проценти нараховуються тільки на по­чаткову суму, проценти, що нараховані в кожному періоді нарахування процентів, дорівнюють: PV i.

Тому, нарощена вартість грошей (FV) за nперіодів нарахування процентів розраховується:

FV=PV+ 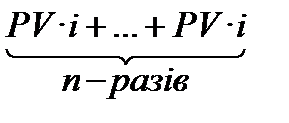=PV+PV·i·n=PV·(1+i·n),(2.1)

де PV∙i∙n ─ сума процентів за n періодів нарахування.

З аналізу поступового розв’язку Модельної задачі 1 (розв’язку по періодам нарахування процентів), а також,керуючись розрахунком (2.1), можемо записати формулу простого нарахування процентів:

FV = PV·(1+i·n), (2.2)

де FV – майбутня вартість у грошових одиницях (докладніше дивися початок підрозділу 1.6);

PV – початкова вартість у грошових одиницях (докладніше дивися початок підрозділу 1.6);

i– процентна ставка у кожному з періодів нарахування процентів n (але у формулі (2.2) процентна ставка i стає показником, що не має розмірності, тобто у формулі показник i використовується не у відсотках, а в частках, в долях, «як темп»);

n – кількість періодів нарахування процентів впродовж часу (строку) застосування ставки і; також, у кожному з цих періодів процентні ставки відповідні періодам та рівні між собою.

У запису формули (2.2) показник (1 + і · n) в лексиці фінансових розрахунків має свою окрему назву ─ множник нарощення простих процентів, або англ. ─ simple interest factor, звідки стає зрозумілою позначка ─ 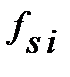. Формулу (2.2) можемо записати у вигляді:

FV = PV · 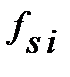. (2.3)

Зазвичай у фінансах використовують формулу (2.2), з (2.3) працюють при наявності фінансових таблиць.

Формула (2.2) відображає 2-й варіант співвідношення між періодом нарахування процента і строком, а саме, що період нарахування процента менше за строк і при цьому тривалість періоду кратна строку, тобто строк має цілу кількість періодів. Проте, формула (2.2) використовується не тільки, коли кількість періодів нарахування процентів (n) є кількісно цілим показником. Формула (2.2) ─ універсальна і використовується, коли n має цілу і дробову частини, або, коли n має дробове значення (див. пункти 2.1.2 та 2.1.4).

В Модельній задачі 1 період нарахування процентів ─ рік, строк ─ чотири роки, кількість періодів нарахування процентів (n) дорівнює цілій кількості періодів ─ чотирьом. Отже, можемо використати формулу (2.2) в розв’язуванні Модельної задачі 1.

Використовуючи (2.2), розв’язок Модельної задачі 1 стає коротеньким:

FV = 1000 грн ∙(1 + 0,1∙4) = 1400 грн.

Відповідь:вМодельній задачі 1 фактична загальна сума грошей, що Ви одержите по закінченні чотирьох років будеFV = 1400 грн.

Формулу (2.2) використовують тоді і лише тоді коли в кожному періоді нарахування процентів процентні ставки (і) рівні між собою (постійні ставки).

Коли процентні ставки в кожному з періодів нарахування різняться, тобто, якщо процентна ставка перемінна, а саме:

─ протягом 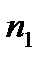періодів процентна ставка дорівнює ,

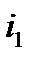─ протягом 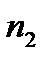періодів процентна ставка дорівнює ,

……………………………………………………………

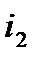─ протягом 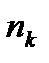періодів процентна ставка дорівнює ,

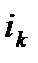то формула простого нарахування процентів приймає вигляд:

FV=PV·(1+ 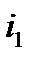· 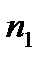+ 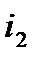· 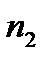+ …+ 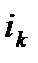· 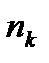)=PV·(1+ 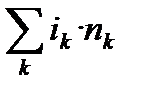).(2.4)

Формула (2.4) ─ це формула для обчислення нарощеної суми грошей у випадку використання схеми нарахування простих про­центів при різних в періодах нарахування процентних ставках (перемінних ставках).

Формула (2.4) відображає (див. стор. 51) 2-й варіант співвідношення між періодом нарахування процента і строком, а саме, що період нарахування процента менше за строк і при цьому тривалість періоду кратна строку, тобто строк має цілу кількість періодів. Також, вона працює і тоді, коли тривалість періоду нарахування процентів має дробовий показник, або ціле число з дробом, тобто 3-й і 4-й варіанти співвідношення між періодом і строком.

Читайте також:

1. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
2. Абсолютний фагоцитоз або елімінуюча здатність крові (ЕЗК) — це кількість фагоцитованих мікробних клітин лейкоцитами 1 мкл крові.
3. Амортизація основних фондів підприємства. Методи нарахування амортизації
4. Амортизація основних фондів підприємства. Методи нарахування амортизації.
5. Амортизація основних фондів, методи її нарахування.
6. Амортизація. Методи нарахування амортизації.
7. Ануїтети з безперервним нарахуванням процентів
8. Ануїтети з виплатами в середині періодів
9. Біомаса - Кількість живої речовини на одиниці площі чи об'єму місцеперебування в момент спостереження. Визначається сумою біомаси усіх популяцій, що населяють дану екосистему.
10. Бухгалтерський облік номіналу депозиту та нарахування процентів за депозитом
11. В межах наукового підходу існує велика кількість концепцій, але найбільш переконлива – еволюційна теорія.
12. В однакових об'ємах різних газів за однакових умов (температура і тиск) міститься однакова кількість молекул.

Переглядів: 441