
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Складне нарахування процентів: ціла і дробова кількість періодів нарахування процентів.
Якщо період нарахування процентів менше за строк фінансової операції і при цьому тривалість періоду не кратна строку, тобто строк має цілу кількість періодів і ще часинку наступного (цілу і дробову) ─ (3-й варіант, див. стор. 51), то застосовується не формула (2.10), а інша, що походить від (2.10) формула, яку надалі будемо називати: формула змішаного нарахування процентів.
При нарахуванні складних процентів за цілу й дробову кількість періодів нарахування процентів застосовується так звана змішана схема, що передбачає нарахування складних процентів за ціле число періодів нарахування й простих процентів за дробову частину періоду нарахування. Розглянемо механізм змішаного нарахування процентів за допомогою розв’язування Модельної задачі 3.
Умови Модельної задачі 3.
Банк видав позику (кредит) у розмірі 500 тис. грн на строк 2 роки й 4 місяці. Процентна ставка ─ 40%. Яку суму поверне боржник банку наприкінці строку при періодах нарахування процентів: а) щорічних, б) по півріччям, в) щоквартальних?
Розв’язання Модельної задачі 3.
Розглядаємофінансову операцію по періодах нарахування процентів. Ставка ─ річна, механізм нарахування ─ складний (згідно неоголошеним правилам).
а) Нарахування процентів щорічне.
ПЕРІОД 1 (перший рік): на початку першого року видано кредит ─ 500 тис. грн; в кінці першого року у позичальника перед банком борг зростає на суму процента, ─ розрахунок в періоді 1: 500 тис. грн. + 500 тис. грн. 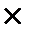 0,4 = 500 тис. грн
0,4 = 500 тис. грн  (1+0,4) = 700 тис. грн.
(1+0,4) = 700 тис. грн.
В кінці першого періоду (першого року) борг перед банком ─ 700 тис. грн, ця ж сума є базою для нарахування процентів у другому періоді.
ПЕРІОД 2 (другий рік): на початку другого року борг перед банком 700 тис. грн; в кінці другого року у позичальника перед банком борг зростає на суму процента, розрахованого від бази ─ 700 тис. грн. Розрахунок в межах періоду 2: 700 тис. грн + 700 тис. грн  0,4 = 700 тис. грн
0,4 = 700 тис. грн 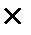 (1+0,4) = 980 тис. грн.
(1+0,4) = 980 тис. грн.
Вище проведений розрахунок можна записати інакше:
500 тис. грн·(1+0,4)·(1+0,4) = 500 тис. грн · (1+0,4) 2 = = 500 тис. грн. · 1,96 = 980 тис. грн.
Отже, на кінець другого року борг перед банком 980 тис. грн. Розрахована сума є базою для розрахунку проценту у наступному періоді.
ПЕРІОД 3 (третій рік): на початку третього року борг перед банком 980 тис. грн. Третій рік, (період нарахування), ─ не повний, а частина року ─ 4 місяці. Протягом 4-х місяців нарахування процентів відбувається на суму 980 тис. грн. Звісно, якби період нарахування був повним, то розмір проценту був би таким: 980 тис. грн 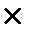 0,4 = 352 тис грн, але період нарахування складає лише частину від повного періоду (року), а саме ─ 4/12. Отже, за ці 4 місяці і процент буде не 352 тис. грн, а 4/12 від 352 тис. грн. Запис розрахунку процента за 4 місяці має такий вигляд: 980 тис. грн
0,4 = 352 тис грн, але період нарахування складає лише частину від повного періоду (року), а саме ─ 4/12. Отже, за ці 4 місяці і процент буде не 352 тис. грн, а 4/12 від 352 тис. грн. Запис розрахунку процента за 4 місяці має такий вигляд: 980 тис. грн 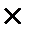 0,4 · 4/12 = 130,7 тис. грн. Тоді, сума боргу перед банком на кінець строку становить:
0,4 · 4/12 = 130,7 тис. грн. Тоді, сума боргу перед банком на кінець строку становить:
980 тис.грн + 980 тис.грн 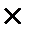 0,4 · 4/12 = 1110,7 тис.грн.
0,4 · 4/12 = 1110,7 тис.грн.
Даний розрахунок можна записати інакше:
500 тис.грн·(1+0,4)·(1+0,4)·(1+0,4·4/12) = 1110,7 тис.грн.
Розрахунок можна записати також і так:
500 тис.грн  (1+0,4)2
(1+0,4)2  (1+0,4·4/12) = 1110,7 тис.грн
(1+0,4·4/12) = 1110,7 тис.грн
При щорічному нарахуванні процентів банк очікує на повернення 1110,7 тис.грн.
В проведеному розрахунку кількість періодів нарахування процентів становить n = 2 цілих 4/12 років. Використовуючи формулу (2.10) розрахунок записується:
FV = 500 тис. грн ·  = 1110,7 тис.грн.
= 1110,7 тис.грн.
б) Нарахування процентів по півріччям.
ПЕРІОД 1 (перше півріччя): на початку першого півріччя видано кредит ─ 500 тис. грн; в кінці першого півріччя у позичальника перед банком борг зростає на суму процента, ─ розрахунок в періоді 1: 500 тис. грн. + 500 тис. грн. 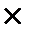 0,4/2 = 500 тис. грн
0,4/2 = 500 тис. грн  (1+0,4/2) = 600 тис. грн.
(1+0,4/2) = 600 тис. грн.
В кінці першого періоду (першого півріччя) борг перед банком ─ 600 тис. грн, ця ж сума є базою для нарахування процентів у другому періоді.
ПЕРІОД 2 (друге півріччя): на початку другого півріччя борг перед банком 600 тис. грн; в кінці другого півріччя у позичальника перед банком борг зростає на суму процента, розрахованого від бази ─ 600 тис. грн. Розрахунок в межах періоду 2: 600 тис. грн + 600 тис. грн  0,4/2 = 600 тис. грн
0,4/2 = 600 тис. грн 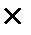 (1+0,4/2) = 720 тис. грн.
(1+0,4/2) = 720 тис. грн.
Даний розрахунок можна записати інакше:
500 тис. грн  (1+0,4/2)
(1+0,4/2)  (1+0,4/2) = 500 тис. грн
(1+0,4/2) = 500 тис. грн  (1+0,4/2) 2 = 500 тис. грн
(1+0,4/2) 2 = 500 тис. грн  1,44 = 720 тис. грн.
1,44 = 720 тис. грн.
На кінець другого півріччя борг перед банком 720 тис. грн.
ПЕРІОД 3 (трете півріччя): на початку третього півріччя борг перед банком 720 тис. грн; в кінці третього півріччя у позичальника перед банком борг зростає на суму процента, розрахованого від бази ─ 720 тис. грн. Розрахунок в межах періоду 3: 720 тис. грн + 720 тис. грн  0,4/2 = 720 тис. грн
0,4/2 = 720 тис. грн 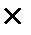 (1+0,4/2) = 720 тис. грн.
(1+0,4/2) = 720 тис. грн.
Даний розрахунок можна записати інакше:
500 тис. грн. · (1+0,4/2) · (1+0,4/2) · (1+0,4/2) = = 500 тис.грн.·(1+0,4/2) 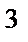 = 500 тис.грн · 1,728 = 864 тис.грн.
= 500 тис.грн · 1,728 = 864 тис.грн.
На кінець третього півріччя борг 864 тис. грн.
ПЕРІОД 4 (четверте півріччя):
500 тис. грн. · (1+0,4/2) · (1+0,4/2) · (1+0,4/2) · (1+0,4/2) = = 500 тис. грн · (1+0,4/2)  = 500 тис. грн · 2,0736 = = 1036,8 тис. грн.
= 500 тис. грн · 2,0736 = = 1036,8 тис. грн.
На кінець четвертого півріччя борг перед банком 1036,8 тис. грн.
Чотири півріччя ─ це два роки. Залишилось 4 місяці наступного півріччя.
ПЕРІОД 5 (п’яте півріччя): на початку п’ятого півріччя борг перед банком 1036,4 тис. грн. П’ятий період нарахування ─ не повний, а лише частина півріччя ─ чотири місяці з шести. Протягом 4-х місяців нарахування процентів відбувається на суму 1036,8 тис. грн. Звісно, якби період нарахування був повним, то розмір проценту був би таким: 1036,8 тис. грн 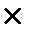 0,4/2 = 207,36 тис грн, але період нарахування складає лише частину від повного періоду (півріччя), а саме ─ 4/6. Отже, за ці 4 місяці і процент буде не 207,36 тис. грн, а 4/6 від 207,36 тис. грн. Запис розрахунку процента за 4 місяці має такий вигляд: 1036,8 тис. грн
0,4/2 = 207,36 тис грн, але період нарахування складає лише частину від повного періоду (півріччя), а саме ─ 4/6. Отже, за ці 4 місяці і процент буде не 207,36 тис. грн, а 4/6 від 207,36 тис. грн. Запис розрахунку процента за 4 місяці має такий вигляд: 1036,8 тис. грн 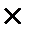 0,4/2 · 4/6 = 138,24 тис. грн. Тоді, сума боргу перед банком на кінець строку становить:
0,4/2 · 4/6 = 138,24 тис. грн. Тоді, сума боргу перед банком на кінець строку становить:
1036,8 тис.грн+1036,8 тис.грн 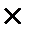 0,4/2·4/6 = 1175,04 тис.грн.
0,4/2·4/6 = 1175,04 тис.грн.
Розрахунок можна записати інакше: 500 тис. грн 
 (1+0,4/2) · (1+0,4/2) · (1+0,4/2) · (1+0,4/2) · (1+0,4/2·4/6) = = 1175,04 тис. грн.
(1+0,4/2) · (1+0,4/2) · (1+0,4/2) · (1+0,4/2) · (1+0,4/2·4/6) = = 1175,04 тис. грн.
Розрахунок можна записати також і так:
500 тис. грн · (1+0,4/2)  · (1+0,4/2·4/6) = 1175,04 тис. грн.
· (1+0,4/2·4/6) = 1175,04 тис. грн.
При піврічному нарахуванні процентів банк очікує на повернення 1175,04 тис. грн.
В проведеному розрахунку:
─ кількість періодів нарахування процентів становить n = 4 цілих 4/6 півріч;
─ процентна ставка в кожному з періодів нарахування процентів і = 0,4/2.
По аналогії з (2.10) розрахунок записується:
FV = 500 тис. грн · 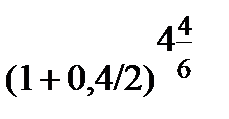 = 1175,04 тис.грн.
= 1175,04 тис.грн.
в) Нарахування процентів щоквартальне.
ПЕРІОД 1 (перший квартал): на початку першого кварталу видано кредит ─ 500 тис. грн; в кінці першого кварталу у позичальника перед банком борг зростає на суму процента, ─ розрахунок в періоді 1: 500 тис. грн. + 500 тис. грн.  0,4/4 = 500 тис. грн
0,4/4 = 500 тис. грн  (1+0,4/4) = 550 тис. грн.
(1+0,4/4) = 550 тис. грн.
В кінці першого періоду (першого кварталу) борг перед банком ─ 550 тис. грн, ця ж сума є базою для нарахування процентів у другому періоді.
ПЕРІОД 2 (другий квартал): на початку другого кварталу борг перед банком 550 тис. грн; в кінці другого кварталу у позичальника перед банком борг зростає на суму процента, розрахованого від бази ─ 550 тис. грн. Розрахунок в межах періоду 2: 550 тис. грн + 550 тис. грн  0,4/4= 550 тис. грн
0,4/4= 550 тис. грн 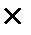 (1+0,4/4) = 605 тис. грн.
(1+0,4/4) = 605 тис. грн.
Даний розрахунок можна записати інакше:
500 тис. грн. · (1+0,4/4)  (1+0,4/4) = 500 тис. грн
(1+0,4/4) = 500 тис. грн  (1+0,4/4) 2 = 500 тис. грн.
(1+0,4/4) 2 = 500 тис. грн.  1,21 = 605 тис. грн.
1,21 = 605 тис. грн.
На кінець другого півріччя борг перед банком 605 тис. грн.
ПЕРІОД 3 (третій квартал), розрахунок:
500 тис. грн.  (1+0,4/4)
(1+0,4/4)  (1+0,4/4)
(1+0,4/4)  (1+0,4/4) = = 500 тис.грн
(1+0,4/4) = = 500 тис.грн  (1+0,4/4)
(1+0,4/4) 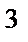 = 500 тис.грн
= 500 тис.грн  1,331 = = 665,5 тис.грн.
1,331 = = 665,5 тис.грн.
На кінець третього півріччя борг перед банком 665,5 тис. грн.
Загалом, у пункті в) Модельної задачі 3 періодів нарахування процентів ─ десять, відповідно кількості кварталів, і в тому числі дев’ять повних (цілих) кварталів і один останній, десятий, не повний ─ що має один місяць із трьох (квартал має три місяці).
ПЕРІОД 9 (дев’ятий квартал), розрахунок за логікою попередніх періодів:
500 тис. грн · (1+0,4/4) · (1+0,4/4) · (1+0,4/4) · (1+0,4/4) ·
· (1+0,4/4) · (1+0,4/4) · (1+0,4/4) · (1+0,4/4) · (1+0,4/4) =
= 500 тис. грн · (1+0,4/4) 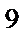 = 500 тис. грн · 2,357947691 = = 1178,974 тис. грн.
= 500 тис. грн · 2,357947691 = = 1178,974 тис. грн.
ПЕРІОД 10 (десятий квартал), розрахунок розглянемо знову детально. На початку десятого кварталу борг перед банком 1178,974 тис. грн. Десятий період нарахування ─ не повний, а лише частина кварталу ─ один місяць із трьох. Протягом цього 1-го місяця нарахування процентів відбувається на суму 1036,8 тис. грн. Звичайно, якби період нарахування був повним (3 місяці), то розмір проценту був би таким: 1178,974 тис. грн 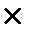 0,4/4 = 117,90 тис грн, але період нарахування складає лише частину від повного періоду (кварталу), а саме ─ 1/3. Отже, за один місяць процент буде не 117,90 тис. грн, а 1/3 від 117,90 тис. грн. Запис розрахунку процента за один місяць має такий вигляд: 1178,974 тис. грн
0,4/4 = 117,90 тис грн, але період нарахування складає лише частину від повного періоду (кварталу), а саме ─ 1/3. Отже, за один місяць процент буде не 117,90 тис. грн, а 1/3 від 117,90 тис. грн. Запис розрахунку процента за один місяць має такий вигляд: 1178,974 тис. грн 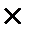 0,4/4 · 1/3 = 39,30 тис. грн. Тоді, сума боргу перед банком на кінець строку становить:
0,4/4 · 1/3 = 39,30 тис. грн. Тоді, сума боргу перед банком на кінець строку становить:
1178,974 тис. грн + 1178,974 тис. грн 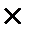 0,4/4 · 1/3 = = 1218,273 тис. грн.
0,4/4 · 1/3 = = 1218,273 тис. грн.
Розрахунок можна записати інакше: 500 тис. грн 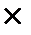
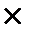 (1+0,4/4)
(1+0,4/4)  (1+0,4/4)
(1+0,4/4)  (1+0,4/4)
(1+0,4/4)  (1+0,4/4)
(1+0,4/4)  (1+0,4/4)
(1+0,4/4)  (1+0,4/4)
(1+0,4/4)  (1+0,4/4)
(1+0,4/4)  (1+0,4/4)
(1+0,4/4)  (1+0,4/4)
(1+0,4/4)  (1+0,4/4·1/3)= = 1218,273 тис. грн.
(1+0,4/4·1/3)= = 1218,273 тис. грн.
Розрахунок можна записати також і так:
500 тис. грн  (1+0,4/4)
(1+0,4/4) 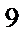
 (1+0,4/4·1/3) = 1218,273 тис. грн.
(1+0,4/4·1/3) = 1218,273 тис. грн.
При щоквартальному нарахуванні процентів банк очікує на повернення 1218,273 тис. грн.
В проведеному розрахунку:
─ кількість періодів нарахування процентів становить n = 9 цілих 1/3 кварталів;
─ процентна ставка в кожному з періодів (кварталів) нарахування процентів і = 0,4/4.
Використовуючи формулу (2.10) розрахунок записується:
FV = 500 тис. грн · 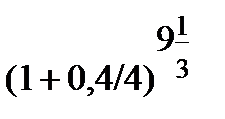 = 1218,273 тис.грн.
= 1218,273 тис.грн.
Всі три варіанти а), б), в) розв’язання Модельної задачі 3 завершилися записом розрахунку у вигляді формули (2.10) в записі якої з’явилася особливість. Показник кількості періодів нарахування n має цілу і дробову частини. Позначимо цілу частину кількості періодів через k,а дробову – через f, тоді n = k + f. При такому n формула (2.10) трансформується, перетворюється хоча і в споріднену до (2.10), але в іншу формулу, яка має назву ─ ФОРМУЛА ЗМІШАНОГО НАРАХУВАННЯ ПРОЦЕНТІВ:
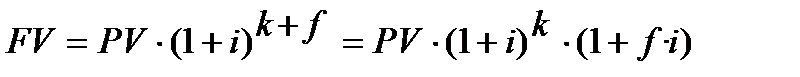 , (2.15)
, (2.15)
деFV, PV, i – мають зміст той же, що й у формулах (2.2), (2.10);
k – ціла частина кількості періодів нарахування;
f – дробова частина кількості періодів нарахування процентів.
Модельна задача 3 розв’язується за допомогою формули (2.15) стисло і швидко:
а) нарахування процентів щорічне:
FV = 500 тис. грн ·  =
=
= 500 тис. грн · (1+0,4) 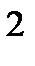 · (1+0,4 ·
· (1+0,4 · 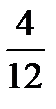 ) = 1110,7 тис. грн.
) = 1110,7 тис. грн.
б) нарахування процентів по півріччям:
FV = 500 тис. грн · 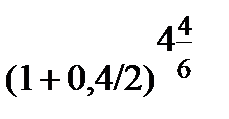 =
=
= 500 тис. грн · (1+ 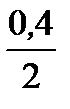 )
)  · (1+
· (1+  ·
·  ) = 1175,04 тис. грн.
) = 1175,04 тис. грн.
в) нарахування процентів щоквартальне:
FV = 500 тис. грн · 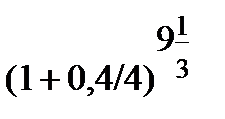 =
=
= 500 тис. грн · (1+ 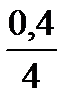 )
) 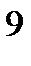 · (1+
· (1+ 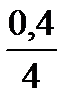 ·
· 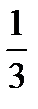 ) = 1218,273 тис. грн.
) = 1218,273 тис. грн.
В посібнику навмисно надано детальне розв’язування Модельної задачі 3. Автор не випадково витратив близько шести сторінок тексту, в яких велися розрахунки без використання відомих до цього моменту формул. Посилання на формулу з’явилося в кінці розрахунку, бо, безпосередньо, сам хід фінансових розрахунків приводив нас до запису розрахунку у формалізованому вигляді. Хід розрахунків «народжує» формулу, а не навпаки. Спочатку, на практиці, людство виконувало розрахунки, а потім, для полегшення розрахунків, винаходило формули. Такій підхід і така поетапна демонстрація розв’язку Модельної задачі 3 дає можливість розвіяти деякі міфи відносно застосування формули (2.15).
_Додаткова інформація_________________________
При застосуванні у фінансових розрахункахформули (2.15) звертають увагу на наступне.
Якщо загальна кількість періодів нарахування має ціле число і залишок, то для цілого числа періодів використовується формула складних процентів, а для залишку ─ або формула складних, або формула простих процентів, однак останнє застосовується частіше. Таким чином, якщо k ─ ціла кількість, а f ─ частина не повного періоду нарахування, то формула (2.15) приймає вид:
─ при застосуванні механізму простих процентів в частині не повного періоду нарахування:
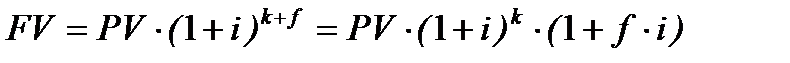 ;
;
─ при застосуванні механізму складних процентів в частині не повного періоду нарахування:
 .
.
Міф перший полягає в тому, що для останнього не цілого періоду нарахування можливі два способи розрахунку, ─ простий, що має вигляд (1+f·i), та складний, що має такий вигляд ─  .
.
Це зовсім не так. Механізм розрахунку складного нарахування процентів показує, що складне нарахування, ─ це нарахування (перемноження) попередніх періодів нарахування на наступний, це нарощення періодами нарахування. Лише коли період нарахування закінчується тільки тоді база помножується на множник періоду нарахування (тобто зростає база). Складне нарахування процентів, це нарахування по періодам нарощення, умовно можна сказати, це нарахування між періодами нарощення, а ніяк не в межах, не в «середині», не в кордонах кожного окремо взятого періоду нарахування. В «кордонах кожного окремо взятого періоду нарахування», як це не дивно, механізм нарахування процентів завжди простий. Це є ще одним неоголошеним правилом.
З позиції внутрішнього механізму формування множника нарощення у формулі (2.15) останній не повний період нарахування ні чим не відрізняється від попередніх Якщо в «середині», в межах попередніх цілих періодів нарахування, зростання має просту схему, то чому в останньому періоді схема нарахування стає складною? Звичайно, що формування множників в кожному з періодів нарахування проходить за одним і тим же механізмом ─ і не за складним, а за простим. Отже, випадок, коли у формулі (2.15) в «частині не повного періоду нарахування застосовують механізм складних процентів» не відповідає практичним реаліям фінансових розрахунків.
Таким чином, у формулі (2.15) для множника за неповний період нарахуванняне існує «два способи розрахунку, ─ простий, що має вигляд (1+f·i), та складний, що має вигляд  ». Існує лише один спосіб розрахунку, ─ простий, що має вигляд (1+f·i).
». Існує лише один спосіб розрахунку, ─ простий, що має вигляд (1+f·i).
Міф другий. Цілком справедливим є ствердження, що у формулі (2.10) показник кількості періодів нарахування процентів «n» є показником ступеню, ступеню з математичної точки зору. Але у формулі (2.15) показник «n», що має цілу і дробову частину, не є показником ступеню, як в математиці.
Математика ─ це набір різноманітних інструментів. Для конкретної операції беруться не всі, а обираються з переліку лише потрібні інструменти. Дії по розрахунку конкретної фінансової операції вимагають застосування не всіх, а тільки відповідних обчисленню інструментальних математичних засобів. Дії по обчисленню вказують на відповідний інструмент і обирають інструмент для розрахунку, а не навпаки. Не математичні інструменти «головують» у фінансових розрахунках, а фінансові обчислення «обирають і одягають на себе» математичний інструментарій.
В економічних науках і особливо у фінансах часто-густо математична системність подавляє практичну обумовленість.
Ходом фінансових розрахунків склався випадок, коли у формулі (2.10) показник кількості періодів нарахування процентів «n» є в той же час і однім з математичних інструментів ─ показником ступеню. Проте, автоматичне і необґрунтоване перенесення цієї властивості на формулу (2.15) є помилкою. Звичайно, формула (2.15) відображає механізм складного нарахування процентів, складність (а не простоту) механізму нарахування в цій формулі, як і в формулі (2.10), надає добуток множників, що розраховуються в дужках. Але розрахунок в останніх дужках формули (2.15) відрізняється від розрахунку в попередніх дужках.
Якщо у формулі (2.15) всі показники в дужках, крім останнього, чисельно рівні між собою, то виражати їх добуток показником ступеню є цілком обґрунтованим. Остання дужка чисельно відрізняється від попередніх множників і не відноситься, а тому і не включається до попереднього ступеневого ряду, а є окремим показником. У цього окремого і завжди в однині множника є свій окремий показник ступеню ─ він за правилами математики не позначається але завжди мається на увазі ─ цей показник ступеню дорівнює одиниці. Показником ступеню останньої дужки у формулі (2.15) завжди є одиниця, але цю одиницю неможливо додати до показника ступеню попередніх дужок тому що в них різні основи.
У формулі (2.15) позначку, що показує кількість періодів нарахування процентів, а саме ─ (n = k + f), підставляють на місце показника ступеню і тому виникає помилковий висновок, що це показник ступеню, який має цілу k і дробову f частини, і що k ─ показник ступеню, і f також показник ступеню. Але перебіг, логіка фінансових розрахунків показує, що при «і» рівних між собою та при рівних між собою періодах нарахування процентів, k стає показником ступеню, а f ніколи не становиться показником ступеню. Запис n сумою k + f вказує, що k та f мають спільну основу, але ця основа ─ не основа для показника ступеню. Основи для k, як показника ступеню, і для f, як показника ступеню, різні. Залишається інша основа за якою можливе додавання k + f , ─ а саме, що це показник кількості періодів нарахування.
Читайте також:
- Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
- Абсолютний фагоцитоз або елімінуюча здатність крові (ЕЗК) — це кількість фагоцитованих мікробних клітин лейкоцитами 1 мкл крові.
- Амортизація основних фондів підприємства. Методи нарахування амортизації
- Амортизація основних фондів підприємства. Методи нарахування амортизації.
- Амортизація основних фондів, методи її нарахування.
- Амортизація. Методи нарахування амортизації.
- Ануїтети з безперервним нарахуванням процентів
- Ануїтети з виплатами в середині періодів
- Безсполучникове складне речення
- Біомаса - Кількість живої речовини на одиниці площі чи об'єму місцеперебування в момент спостереження. Визначається сумою біомаси усіх популяцій, що населяють дану екосистему.
- Бухгалтерський облік номіналу депозиту та нарахування процентів за депозитом
- В межах наукового підходу існує велика кількість концепцій, але найбільш переконлива – еволюційна теорія.
| <== попередня сторінка | | | наступна сторінка ==> |
| Розв’язання задачі. | | | У формулі (2.15) показник «n», що має цілу і дробову частину, не є показником ступеню, а є показником виключно тільки кількості періодів нарахування процентів. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |