• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розв’язання задачі.

а) Механізм нарахування процентів ─ простий. Використовуємо формулу (2.2):

1) щоквартальне нарахування процентів:

спочатку підготуємо дані, що входять до формули (2.2), за умовами задачі: PV= 2 млн. грн, n розраховуємо знаючи, що рік має 4 квартали, а загальна кількість років 10. Отже, кількість періодів нарахування n = 40, процентна ставка в умові задачі дається, як річна, але для періоду нарахування ─ кварталу процентна ставкаі = 0,15/4. Підготовлені значення підставимо у формулу (2.2):

FV = PV·(1+ i·n) = 2 млн грн · (1 + 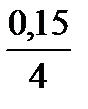· 40) = 5 млн грн.

2) піврічне нарахування процентів:

n розраховуємо знаючи, що рік має 2 півріччя, а загальна кількість років 10. Отже, кількість періодів нарахування (кількість кварталів) n = 20, процентна ставка в умові задачі надається, як річна, отже, для півріччя процентна ставка i =0,15/2. Підготовлені значення підставимо у формулу (2.2), одержимо:

FV = PV·(1+ i·n) = 2 млн грн · (1 + 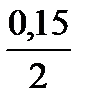· 20) = 5 млн грн.

3) річне нарахування процентів:

n = 10, i = 0,15. Підготовлені значення підставимо у формулу (2.2), одержимо:

FV = PV·(1+ i·n) = 2 млн грн · (1 + 0,15·10) = 5 млн грн.

4) нарахування процентів один раз в 5 років:

nрозраховуємо знаючи, що в 10-ти роках вміщається два періоди по 5 років. Отже, кількість періодів нарахування n = 2, процентна ставка в умові задачі надається, як річна, отже, для п’ятирічного періоду нарахування процентна ставка i = 0,15 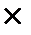5. Підготовлені значення підставимо у формулу (2.2), одержимо:

FV = PV·(1+ i·n) = 2 млн грн · (1 + 0,15 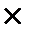5·2) = 5 млн грн.

5) нарахування процентів один раз в 10 років:

n розраховуємо знаючи, що в 10-ти роках вміщується один період з 10 років. Отже, кількість періодів нарахування n= = 1, процентна ставка в умові задачі надається, як річна, отже, для десятилітнього періоду процентна ставка i = =0,15 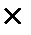10. Підготовлені значення підставимо у формулу (2.2), одержимо:

FV = PV·(1+ i·n) = 2 млн грн · (1 + 0,15 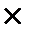10·1) = 5 млн грн.

б) Механізм нарахування процентів ─ складний.

Використовуємо формулу (2.10):

1) щоквартальне нарахування процентів:

Для початку підготуємо дані, що входять до формули (2.10), за умовами задачі: PV= 2 млн. грн, n розраховуємо знаючи, що рік має 4 квартали, а загальна кількість років 10. Отже, кількість періодів нарахування (кількість кварталів) n = 40, процентна ставка в умові задачі дається, як річна, але для кварталу процентна ставкаі = 0,15/4. Підготовлені значення підставимо у формулу (2.10), одержимо:

FV = PV· (1+ і) 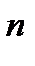= 2 млн грн · (1 + 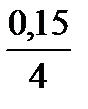) = 8,721 млн грн.

2) піврічне нарахування процентів:

n розраховуємо знаючи, що рік має 2 півріччя, а загальна кількість років 10. Отже, кількість періодів нарахування (кількість півріч) n = 20, процентна ставка в умові задачі надається, як річна, отже, для півріччя процентна ставка i = 0,15/2. Підготовлені значення підставимо у формулу (2.10), одержимо:

FV = PV· (1+ і) 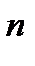= 2 млн грн · (1 + 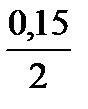) 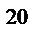= 8,496 млн грн.

3) річне нарахування процентів:

n = 10, i= 0,15. Підготовлені значення підставимо у формулу (2.10), одержимо:

FV = PV· (1+ і) 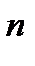= 2 млн грн · (1 + 0,15) 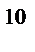= 8,091 млн грн.

4) нарахування процентів один раз в 5 років:

n розраховуємо знаючи, що в 10-и роках є два періоди по 5 років. Отже, кількість періодів нарахування n = 2, процентна ставка в умові задачі надається, як річна, отже, для п’ятирічного періоду процентна ставка i = 0,15 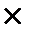5. Підготовлені значення підставимо у формулу (2.10), одержимо:

FV =PV· (1+ і) 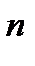= 2 млн грн·(1 + 0,15 5) 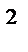= 6,125 млн грн.

5) нарахування процентів раз в 10 років:

n розраховуємо знаючи, що в 10-ти роках вміщується один період з 10 років. Отже, кількість періодів нарахування n = 1, процентна ставка в умові задачі надається, як річна, отже, для десятилітнього періоду процентна ставка i = 0,15 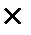10. Підготовлені значення підставимо у формулу (2.10), одержимо:

FV =PV· (1+ і) 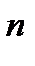= 2 млн грн·(1 + 0,15 10) = 5,000 млн грн.

Аналізуючи розв’язок задачі з Прикладу 2.3, який надано вище, можна зазначити наступне: використання у фінансових розрахунках механізму простих і складних процентів дає неоднакові кінцеві результати.

ВИСНОВОК 1: При використанні механізму простого нарахування процентів поділ строку на більшу кількість періодів нарахування не впливає на розмір нарощеної суми. Нарощена сума FV не змінюється, якщо в межах строку Т кількість періодів нарахування n збільшується або зменшується.

ВИСНОВОК 2: При використанні механізму складного нарахування процентів поділ строку на періоди нарахування впливає на розмір нарощеної суми. Поділ строку Т на більшу кількість періодів нарахування при застосуванні механізму нарахування складних процентів забезпечує більший розмір нарощеної суми. Як бачимо із попередньої задачі, найбільшу «прибавку» в нарощенні дає перехід від n = 1 до n = 2. Подальше зростання n дає меншу суму нарощення по відношенню до попередньої.

ВИСНОВОК 3: Порівнюючи механізми простого та складного нарахування процентів з позиції розрахованих результатів можемо констатувати: механізм простого нарахування процентів завжди надає результат, який дорівнює результату за механізмом складного нарахування процентів при кількості періодів нарахування n = 1 (звісно, при умові тотожності показників PV, Т, і, тривалості періодів нарахування процентів). Прогляньте у Прикладі 2.3 результати всіх розрахунків за механізмом простого нарахування процентів та порівняйте їх з останнім розрахунком, який проведено за механізмом складного нарахування процентів (розрахунок 5) нарахування процентів раз в 10 років). Нарахування за механізмом простого нарахування процентів, це той же розрахунок, що і за механізмом складного нарахування процентів за умови, що період нарахування процентів лише один і завжди один. Отже, можемо зазначити, що при механізмі простого нарахування процентів n охоплює та представляє собою весь строк Т, тобто, що при механізмі простого нарахування процентів n = Т.Тоді формула (2.2) FV = PV·(1+ i·n) може мати і такий запис:

FV = PV·(1+ i·Т) (2.14)

де FV – майбутня вартість у грошових одиницях;

PV – початкова вартість у грошових одиницях;

i– річна процентна ставка, яка застосовується та не змінюється впродовж строку Т ;

Т – строк фінансової операції (в роках), або, що одне і теж, строк (в роках) застосовування річної ставки і.

Читайте також:

1. IV. Перевірка розв’язання і відповідь
2. Алгоритм розв’язання задачі
3. Алгоритм розв’язання розподільної задачі
4. Визначення оптимального варіанта розв’язання проблеми на основі порівняльного аналізу можливих варіантів
5. Визначення проблеми, на розв’язання якої спрямована Програма
6. Відповіді на ситуаційні задачі.
7. Відповіді на ситуаційні задачі.
8. Геофізичний контроль за розробкою нафтових і газових родовищ. Задачі. Методи і методика дослідження
9. Гіпотеза як один із важливих варіантів розв’язання наукової проблеми.
10. Для всіх , та , то він є оптимальним планом транспортної задачі.
11. За допомогою теорії розмірностей розмірні фізичні величини, що входять в опис фізичного процесу, комбінуються в безрозмiрнi комплекси, які можна розглядати як нові змінні задачі.
12. Загальні рекомендації до розв’язання задач

Переглядів: 393