• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

За допомогою теорії розмірностей розмірні фізичні величини, що входять в опис фізичного процесу, комбінуються в безрозмiрнi комплекси, які можна розглядати як нові змінні задачі.

Число таких комплексів завжди менше, ніж число фізичних величин з яких вони складені. Введення таких комплексів можливо як при наявностi системи рівнянь, яка описує фізичний процес, так і без неї, достатньо тільки знати, які фізичні величини входять в опис процесу.

Якщо перелік суттєвих для опису процесу фізичних величин є визначеним, а математичне формулювання у вигляді будь-яких рівнянь відсутнє, числа подібності можуть бути знайдені за допомогою теорії розмірностей, яка встановлює також і кількість чисел подібності, що будуть отримані.

Ця кількість встановлюється так званою ПІ - теоремою, згідно до якої фізичне рівняння, яке має n ³ 2 розмірних величин, з яких k³1 величин мають незалежну розмірність, після приведення до безрозмірного вигляду буде мати n-k - безрозмірних величин.

Перша теорема подібності.

Подібні між собою процеси мають однакові крітерії подібності.

Друга теорема подібності.

Встановлює можливість представлення інтегралу як функції від крітеріїв подібності диференціального рівняння.

Висновок – якщо результати якогось експерименту представлені в крітеріях подібності, вони справедливі для всіх подібних між собою процесів

Третя теорема подібності

Подібні ті фізичні явища, умови однозначності яких подібні, а крітерії, складені з умов однозначності, чисельно однакові.

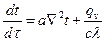При наявності систем рівнянь їх приводять до безрозмірного вигляду, для чого вибирають масштаби незалежних і залежних змінних, спираючись, як правило, на умови однозначності. Покажемо це на прикладі рівняння енергії,

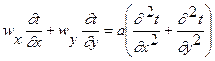для спрощення записаного для двовимірного стаціонарного руху без внутрішніх джерел тепла. Розписуючи повний диференціал температури і оператор Лапласа в такому випадку будемо мати:

Якщо

- за масштаб швидкості обрати швидкість незбуреного потоку wo,

- за масштаб лінійних величин х і у якийсь характерний розмір задачі Lо (довжина або дiаметр каналу, висота стiнки приладу т.i.),

- за масштаб температури - температуру поверхні тіла - tc, то можна записати:

x = X·L0, y = Y · L0, wx = Wx · w0, wy = Wy · w0, t= Θ · tc,

де X, Y, Wx, Wy, Θ - будуть безрозмірними величинами.

Підставляючи їх в рівняння енергії отримаємо:

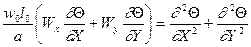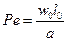Це рівняння є безрозмірним і має один безрозмірний комплекс, який позначають

і називають числом (або крітерієм) Пеклє.

Враховуючи, що розмірності ν і а однакові, він може бути записаний у вигляді:

Де

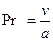- крітерій Рейнольдса,

- крітерій Прандтля.

Аналогічна процедура, проведена для рівняння руху дасть безрозмірні числа:

вже отримане раніше число Рейнольдса;

число Грасгофа -

в яке входять: - прискорення сил тяжіння і

- характерна різниця температур

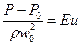(наприклад, це може бути різниця температур стінки і незбуреного потоку рідини);

- Число Ейлера, ро - якесь фіксоване значення тиску, наприклад на вході в канал.

Гранична умова, приведена до безрозмірного вигляду, буде мати вигляд:

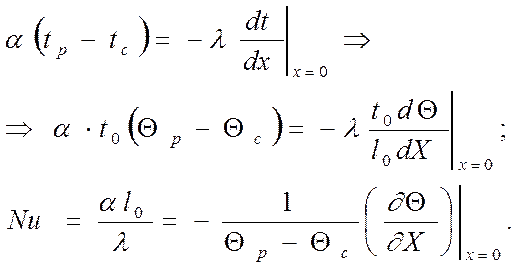
де -

- число Нусельта.

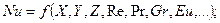
Таким чином, якщо за основний результат вважати визначення коефіцієнта тепловіддачі, який входить в основні формули розрахунку теплопередачі та граничні умови задач нестаціонарної теплопровідності, її розв’язок можна представити у вигляді

Основним практичним висновком з вищеприведеного є встановлення можливостi перенесення результатiв експериментальних дослiджень при певних значеннях безрозмiрних чисел (критерiїв) на iншi процеси, якi мають такi ж значення безрозмiрних чисел та є подiбними до процесу, що дослiджувався експериментально.

Критерії (числа) подібності мають певний фізичний зміст.

Критерій Нусельта є відношенням інтенсивності тепловіддачі a до теплопровідності рідини λ .

Критерій Рейнольдса є мірою відношення інерційних сил до сил тертя.

Критерій Прандля характеризує фізичні властивості рідини та співвідношення товщин гідродинамічного та температурного шарів.

Критерій Грасгофа характеризує співвідношення піднімальної сили до сил тертя

Таким чином теорія подібності дозволяє, не розвязуючи диференціальних рівнянь, отримати критерії подібності і на підставі згаданих вище теорем організувати експериментальні дослідження та отримати явний вигяд критеріальних залежностей, які будуть справедливі для всіх подібних між собою процесів.

Треба підкреслити, що отримані залежності можна використовувати тільки в тому діапазоні параметрів, в якому були проведені експериментальні дослідження, вихід за оговорені межі може призвести до суттєвих похибок.

При обробці експериментальних даних треба розв’язати декілька питань відносно визначення геометричних розмірів і властивостей, які обумовлюють задачу.

Так як при теплообміні температура рідини змінюється як по перерізу, так і вздовж каналу, стінки, приладу, то змінюються і фізичні властивості рідини. Тому при обробці експериментальних даних важливо правильно вибрати температуру, при якій визначаються фізичні властивості задачі.

Така температура має назву визначаюча температура.

Знайти якусь температуру, яка б автоматично враховувала всі особливості задачі неможливо і тому частіше за все такою визначаючою температурою вибирається така, яка в технічних розрахунках була б задана або легко визначалась. Інколи визначаюча температура є функцією розв’язку задачі і тоді при обчисленнях потрібні 2–3 ітераційні наближення.

Другою важливою величиною є геометричний параметр задачі - визначальний розмір.В деяких випадках вибір визначального розміру є очевидним, наприклад, в круглій трубі - це її внутрішній діаметр, при обтіканні пластини - її довжина.

• Для каналів некруглої форми за визначальний розмір беруть умовний діаметр – еквівалентний діаметр, який дорівнює чотирьом площам перерізу канала, перпендикулярно до направлення потоку, віднесений до периметру каналу, який є змоченим рідиною, незалежно від того, яка частина каналу приймає участь в теплообміні.

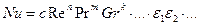• Результати обробки представляються як залежності між критеріями у вигляді степінних функцій. Так як результатом обчислень завжди є коефіцієнт тепловіддачі, який входить в критерій Нульсета, Nu, то формули майже завжди мають вигляд:

•

•

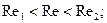• де c, n, k, m - числові коефіцієнти; Re1,2; Gr1,2 Pr1,2 - межі в яких можна використовувати форулу; eі - поправочні коефіцієнти, які вводять для уточнення впливу якихось відмінних від визначених температур та розмірів, визначення впливу напрямку теплового потоку і таке інше. Поправки на вплив температури, напрямку теплового потоку можуть мати різну форму, інколи додаються у вигляді таблиць та графіків.

Найбільш важливою є поправка, яка враховує напрямок теплового потоку.

Частіше ця поправка є функцією відношенням фізичних параметрів при температурі стінки до них же при температурі рідини, що дозволяє враховувати напрямок теплового потоку. Для рідин частіше за все вживають поправку

де Рrp,c - величина Рr обчислена при температурі рідини і стінки. Інколи поправка має вигляд відношення тільки динамічної вязкості ; де n - числовий коефіцієнт.

Для газів така поправка непотрібна при різницях температур між стінкою та газом в 100-200 , так як фізичні властивості газів несуттєво залежать від температур. Для більших різниць використовується поправка у вигляді

Відмітимо, що зміна напрямку руху теплового потоку може змінити величину коефіцієнта тепловіддачі на 10 - 30 %, особливо для вязких речовин - масел, нафти та навiть води.

Читайте також:

1. II. За зміною ступенів окиснення елементів, які входять до складу реагуючих речовин
2. Internet. - це мережа з комутацією пакетів, і її можна порівняти з організацією роботи звичайної пошти.
3. А .Маршалл - основоположник неокласичної теорії.
4. А/. Фізичні особи як суб’єкти цивільного права.
5. Агрегатний індекс фізичного обсягу
6. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
7. Активні інгредієнти, що входять до складу препаратів для симптоматичного лікування лихоманки.
8. Активні інгредієнти, що входять до складу препаратів для симптоматичного лікування сухого кашлю.
9. Альтернативні теорії вартості
10. Альтернативні теорії капіталу
11. Альтернативні теорії макроекономічного регулювання
12. Альтернативні теорії максимізації

Переглядів: 1676