Орієнтовані графи

Введемо основні поняття і терміни, пов’язані з орієнтованими графами. Вони мають додаткову характерну особливість, яка полягає в тому, що на кожному ребрі задається напрям, тобто вказано, яку вершину вважають початком ребра, а яку кінцем. Саме ребро називають орієнтованим.

Визначення 2.9. Граф, всі ребра якого орієнтовані, називається орієнтованим графом (орграфом).

Таким чином, різниця між неорієнтованим і орієнтованим графами полягає в тому, що в першому випадку граничні точки ребра утворюють невпорядковану, а в другому — впорядковану пару вершин. Тому ряд понять, введених для неорієнтованих графів, переносяться аналогічно і на орієнтовані.

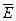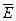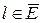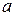Подібно до визначення 2.1, орієнтований граф складається з непорожньої множини V, множини , яка не перетинається з V і між якими визначено відношення інцидентності . Елементи V і , відповідно називаються вершинами і дугами (або напрямними ребрами), а — орієнтованим відображенням інцидентності орієнтованого графа. Якщо і , то кажуть, що дуга має початкову вершину 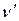і кінцеву .

Орієнтовані графи позначаються . Тоді неорієнтований граф, згідно зі сказаним вище, отримується з орієнтованого відкиданням вимоги впорядкованості.

Зауважимо, що якщо не задано в явному виді, то замість пишуть .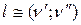

Досить часто визначення понять орієнтованого графа вводять на основі відповідних понять для неорієнтованого. Наприклад, дві дуги графа D називаються паралельними, якщо відповідні їм ребра неорієнтованого графа G паралельні.

Оскільки для орієнтованого графа одна і та сама вершина може служити початком для одних ребер і кінцем для інших, то відповідно розрізняють два степені вершини графа: степінь виходу і степінь входу.

Визначення 2.10. Степенем виходу вершини А орієнтованого графа називається число ребер, які виходять з вершини А.

Відповідно, степінь входу вершини А — це число ребер, які входять в вершину А.

В орієнтованих графах для його вершин можливі ситуації:

а) вершина – ізольована, якщо степінь входу і степінь виходу рівний нулю;

б) вершина – джерело, якщо степінь виходу додатній, а степінь входу рівний нулю;

в) вершина – стік, якщо степінь входу додатній, а степінь виходу нуль.

Визначення 2.11. Шляхом в орієнтованому графі D від до 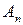називається послідовність орієнтованих ребер ( ; ), ( ; 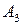),...,( 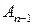; 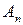)така, що кінець кожного попереднього ребра співпадає з початком наступного і жодне ребро не зустрічається більше одного разу.

Зауважимо, що якщо в орієнтованому графі існує шлях від А до В, то шляху від В до А може і не бути.

Якщо існує орієнтований шлях від А до В, то кажуть, що В досяжна з А.

Визначення 2.12. Простим шляхом в орієнтованому графі називається шлях, в якому кожна вершина не міститься більше одного разу.

Під довжиною шляху розуміють число орієнтованих ребер в цьому шляху. Шлях називають замкненим, якщо початкова і кінцева вершини співпадають і незамкненим в іншому випадку. Замкнений шлях в орієнтованому графі називається орієнтованим циклом.

Відстанню від А до В в орієнтованому графі називають довжину найкоротшого шляху від А до В. Якщо шляху від А до В не існує, то відстань від А до В називають нескінченною.

Визначення 2.13. Повним орієнтованим графом називається граф, кожна пара вершин якого з’єднана одним і тільки одним орієнтованим ребром.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Неорієнтовані графи	\|	Матричне представлення графів

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.003 сек.