МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Матричне представлення графів
У випадку великої кількості вершин і дуг рисунок графа перестає бути наглядним. Тому для його задання використовують матриці. Найбільш вживаними в цьому плані є матриці суміжності, інцидентності, шляхів, циклів, перерізів. Більш детально зупинимося на перших трьох видах матриць.
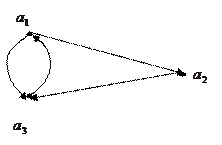 Так для графа
Так для графа 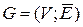 з n вершинами матриця суміжності є розмірності
з n вершинами матриця суміжності є розмірності  , а її елементи
, а її елементи  задаються формулою
задаються формулою

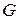
Наприклад, для графа  матриця суміжності має вигляд
матриця суміжності має вигляд

Матриця інцидентності орієнтованого графа, складається з n стовпчиків і k рядків, де n – число вершин графа, а k – число дуг цього графа (пронумеруємо їх 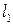 ,
,  ,…,
,…,  ). Елементи матриці
). Елементи матриці  знаходяться за формулою:
знаходяться за формулою:

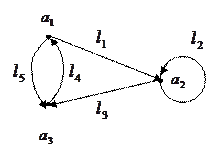 Для графа
Для графа
матриця інцидентності має вигляд

Для зв’язного графа, вершини якого перенумеровані, можна побудувати матрицю шляхів S наступним чином: рядки матриці повинні відповідати шляхам з першої вершини в останню, а стовпчики ребрам графа. Відповідно елемент матриці приймає значення 1 або 0 в залежності від того належить ребро графа даному шляху чи ні.
Так для графа
 |
|
|
|
|
|
всеможливими шляхами є  ,
,  ,
, 
 а матриця шляхів має вигляд
а матриця шляхів має вигляд
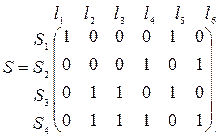
Мережі
Розглянемо орієнтовані зв’язні графи, які не мають петель. Їх називатимемо мережами. Оптимізаційні задачі на мережі можна описати наступними типами моделей.
Читайте також:
- Графічне представлення енергії
- ЕЛЕКТРИЧНІ СИГНАЛИ. СПЕКТРАЛЬНЕ ПРЕДСТАВЛЕННЯ СИГНАЛІВ
- Знання і їхнє представлення в СШІ
- Зображення графів
- Канали представлення і замовлення послуг.
- Культура поведінки соціального працівника з клієнтом: знайомство, вітання, представлення, звертання, спілкування тощо
- Матричне подання циклічних кодів
- Метод побудови прогнозних графів
- НАОЧНЕ ПРЕДСТАВЛЕННЯ ПСИХОДІАГНОСТИЧНИХ ДОСЛІДЖЕНЬ
- Нуль-полюсне представлення характеристик коливального контуру
- Організація і представлення даних. Файл. Файлова система. Ім’я файлу, шлях до файлів. Властивості файлів.
| <== попередня сторінка | | | наступна сторінка ==> |
| Орієнтовані графи | | | Мінімізація мережі |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |