• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

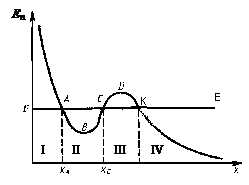
Графічне представлення енергії

В багатьох практичних задачах береться, що потенціальна енергія є функцією лиш однієї змінної (наприклад, координати 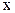), тобто 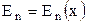. Якщо система консервативна, то для неї справедливий закон збереження повної механічної енергії .

Графік залежності 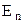від називається потенціальною кривою (рис.1.14).

Повна механічна енергія визначається прямою паралельною до осі абсцис. Потенціальна енергія 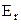ви-значається відрізком вертикалі між точкою на осі абсцис і графіком 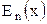. Кінетична енергія визначається відрізком вертикалі між графіком 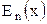і прямою .

Аналіз потенціальних кривих позволяє визначити характер руху тіла. Якщо 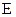– задана повна механічна енергія, то тіло

Рис.1.14 може рухатися тільки там, де , тобто в областях II і

IV. В області I і III тіло проникнути не може, так як потенціальна енергія не може стати більшою за повну (бо кінетична енергія не може бути від’ємною). Область II називають потенціальною ямою. Область III називають потенціальним бар’єром, через який тіло не може проникнути, маючи даний запас повної енергії. Рухаючись в області IV тіло може віддалитися на нескінченність. Такий рух називають інфінітним. Рухаючись в області потенціальної ями, тіло не може віддалитись на нескінченність; такий рух називають фінітним.

Повернемось до формули 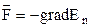, яка виражає зв’язок між консервативною силою і потенціальною енергією. В одновимірному русі вона приймає вигляд .

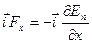Якщо , то , що дає умову рівноваги тіла. Рівновага може бути стійкою або нестійкою. Рівновага буде стійкою, коли потенціальна енергія мінімальна (наприклад, точка В) і нестійкою, коли потенціальна енергія максимальна (наприклад, точка Д).

Читайте також:

1. III. За виділенням або поглинанням енергії
2. IV. Критерій питомої потенціальної енергії деформації формозміни
3. Вигідне господарсько-географічне розташування Харкова перетворило його у XVIIІ ст. на один з найпотужніших економічних центрів Російської імперії.
4. Видання. Поліграфічне виконання. Терміни та визначення
5. Визначення ймовірності перерви електропостачання і середньої кількості недоотриманої електроенергії.
6. ВИКОРИСТАННЯ СВІТЛОВОЇ ЕНЕРГІЇ ГАЛОБАКТЕРІЯМИ
7. Вимірювання енергії
8. Вимірювання потужності та енергії на високих частотах
9. Врахування витраті втрат електроенергії. Приклад складання електробалансу.
10. Втрати енергії вздовж круглого трубопроводу. Формула Пуазейля і коефіцієнт Дарсі.
11. Втрати потужності та енергії в лініях
12. Вчення про економіко-географічне положення (ЕГП).

Переглядів: 847