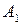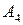РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Потоки в мережах
Надалі, щоб відрізнити орієнтований граф  від мережі, позначатимемо мережу
від мережі, позначатимемо мережу  .
.
Визначення 2.14. Потоком в мережі  називається цілочислова функція
називається цілочислова функція 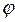 визначена на
визначена на 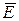 .
.
Ціле число  називається потоком по дузі
називається потоком по дузі 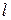 . Більш точно, якщо
. Більш точно, якщо 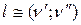 , то кажуть, що потік напрямлений від
, то кажуть, що потік напрямлений від 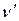 до
до  при
при  і від
і від  до
до 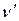 при
при 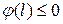 .
.
Величину 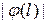 інтерпретують як постійну швидкість потоку однорідної речовини через дугу
інтерпретують як постійну швидкість потоку однорідної речовини через дугу 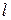 . Напрям потоку визначається знаком
. Напрям потоку визначається знаком  з врахуванням наведених вище умов.
з врахуванням наведених вище умов.
Вершини мережі 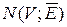 , зазвичай, класифікують за їх впливом на потік
, зазвичай, класифікують за їх впливом на потік 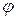 (породжують, поглинають або зберігають потік). Позначимо через
(породжують, поглинають або зберігають потік). Позначимо через 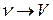 множину дуг, для яких
множину дуг, для яких 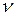 є початковою вершиною, а через
є початковою вершиною, а через 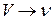 — множину дуг, для яких
— множину дуг, для яких  є кінцевою вершиною. Тоді ціле число
є кінцевою вершиною. Тоді ціле число  , яке визначається співвідношенням
, яке визначається співвідношенням  називається чистим потоком з
називається чистим потоком з  відносно
відносно 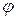 .
.
Якщо  по кожній дузі, то перша сума є загальним потоком, який витікає з вершини
по кожній дузі, то перша сума є загальним потоком, який витікає з вершини  , а друга — загальним потоком, який впадає в вершину
, а друга — загальним потоком, який впадає в вершину 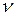 .
.
Якщо по деяких дугах потоки від’ємні, то дані суми не мають наглядної інтерпретації, але їх різниця, як і раніше, є порожнім потоком із вершини 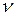 . Надалі чистий потік позначатимемо
. Надалі чистий потік позначатимемо 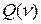 .
.
Згрупуємо вершини мережі  в множини:
в множини:
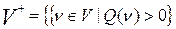 ,
,  ,
,  .
.
Елементи множин 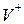 ,
,  ,
,  називаються джерелами, стоками і проміжними вершинами і кажуть, що ці вершини відповідно породжують, споживають і зберігають потік.
називаються джерелами, стоками і проміжними вершинами і кажуть, що ці вершини відповідно породжують, споживають і зберігають потік.
Якщо мережа має єдине джерело  , єдиний стік
, єдиний стік  , і розглядається потік із
, і розглядається потік із  в
в  , то величини
, то величини 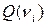 і
і 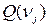 називаються величиною потоку.
називаються величиною потоку.
Нехай  і
і  — потоки в одній і тій же мережі
— потоки в одній і тій же мережі  , а p — ціле число. Тоді для кожної дуги
, а p — ціле число. Тоді для кожної дуги 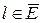 потоки
потоки 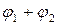 ,
, 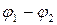 і
і  визначаються за допомогою співвідношень:
визначаються за допомогою співвідношень:
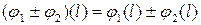 ,
, 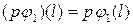 .
.
Будемо писати  тоді і тільки тоді, коли
тоді і тільки тоді, коли  .
.
Кажуть, що потік 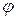 обмежений значеннями
обмежений значеннями  і
і 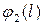 , якщо
, якщо  для кожної дуги мережі.
для кожної дуги мережі.
Потоки  і
і  називаються узгодженими, якщо
називаються узгодженими, якщо 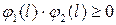 для кожної дуги
для кожної дуги 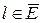 . Іншими словами, потоки
. Іншими словами, потоки  і
і  узгоджені, якщо не існує дуг
узгоджені, якщо не існує дуг 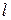 , для яких
, для яких 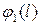 і
і  відмінні від нуля і протилежно напрямлені. Потоки
відмінні від нуля і протилежно напрямлені. Потоки 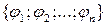 в одній і тій мережі називаються узгодженими в сукупності, якщо вони попарно узгоджені.
в одній і тій мережі називаються узгодженими в сукупності, якщо вони попарно узгоджені.
Нехай в даній мережі  С є множиною дуг, які утворюють простий ланцюг або простий цикл у відповідному неорієнтованому графі. Припустимо, що ми орієнтуємо ребра, проходячи ці прості ланцюги і цикли в одному з можливих напрямків.
С є множиною дуг, які утворюють простий ланцюг або простий цикл у відповідному неорієнтованому графі. Припустимо, що ми орієнтуємо ребра, проходячи ці прості ланцюги і цикли в одному з можливих напрямків.
Визначення 2.15. Дуга із С буде називатися нормальною, якщо її нова орієнтація співпадає з вихідною, і оберненою в іншому випадку.
Визначимо функцію  на
на 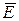 наступним чином:
наступним чином:

На рисунку 2.8 зображений простий ланцюг С, орієнтований з  у
у 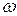 , орієнтований простий цикл S і відповідні функції
, орієнтований простий цикл S і відповідні функції 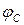 і
і 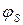 .
.
 | |||
 | |||
Рис.2.8.
 Якщо C – простий ланцюг, який з’єднує v і w і орієнтований від v до w, то
Якщо C – простий ланцюг, який з’єднує v і w і орієнтований від v до w, то 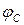 є потоком із v до w, величина якого дорівнює 1. Цей потік називається простим потоком в ланцюзі з v в w. Аналогічно, якщо S — цикл орієнтований в одному з двох напрямків, то
є потоком із v до w, величина якого дорівнює 1. Цей потік називається простим потоком в ланцюзі з v в w. Аналогічно, якщо S — цикл орієнтований в одному з двох напрямків, то 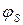 — потік в
— потік в  , величина якого рівна нулю, називається простим потоком по циклу. Потоки цих двох типів (і тільки цих) називаються простими потоками.
, величина якого рівна нулю, називається простим потоком по циклу. Потоки цих двох типів (і тільки цих) називаються простими потоками.
Визначення 2.16. Мережа 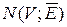 називається мережею з обмеженою пропускною здатністю, якщо на
називається мережею з обмеженою пропускною здатністю, якщо на 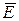 визначені дві функції
визначені дві функції  і
і  , які приймають цілочислові значення, причому
, які приймають цілочислові значення, причому  для всіх
для всіх 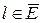 .
.
Цілі числа  і
і  називаються верхньою і нижньою границями пропускної здатності і інтерпретуються як максимально і мінімально допустима величина потоку по кожній дузі. Якщо
називаються верхньою і нижньою границями пропускної здатності і інтерпретуються як максимально і мінімально допустима величина потоку по кожній дузі. Якщо  для всіх
для всіх 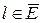 , то
, то  , зазвичай, називають пропускною здатністю дуги
, зазвичай, називають пропускною здатністю дуги 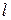 .
.
Визначення 2.17. Потік 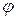 в мережі називається допустимим тоді і тільки тоді, коли
в мережі називається допустимим тоді і тільки тоді, коли 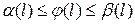 для всіх
для всіх 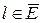 .
.
 Якщо
Якщо  і
і  — допустимі потоки, а
— допустимі потоки, а 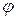 — будь-який потік, обмежений потоками
— будь-який потік, обмежений потоками  і
і  , то
, то 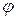 також є допустимим.
також є допустимим.

 Розглянемо мережу, зображену на рисунку 2.9.
Розглянемо мережу, зображену на рисунку 2.9.
| а) | б) |
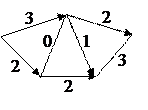
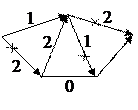
| в) | г) |
| Рис.2.9. |
Наша мета — максимізувати потік з v в w. Очевидно, що максимальна довжина потоку не може бути менша ніж 5 одиниць. Виберемо ланцюг v, у, х, w і припишемо кожній дузі потік величиною 2. Решти дугам припишемо потоки рівні нулю. Отримаємо потік, зображений на рисунку 2.9 б). Візьмемо тепер ланцюг v, х, z, w і припишемо одиничний потік кожній із його дуг. Додавши новий потік до попереднього, отримаємо потік, зображений на рисунку 2.9.в), з трьома насиченими дугами. Єдиний спосіб, з допомогою якого можна збільшити величину потоку з v в w, полягає в тому, щоб відмовитись від раніше прийнятого рішення пропустити потік від у до х. Додамо потік величини 2 в ланцюг v, х, у, z, w. Одержаний в результаті потік, показаний на рисунку 2.9 г) і його величина є максимальною.
Синтез потоків описується з допомогою допоміжного орієнтованого графа, який називається графом приростів. Якщо 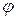 — допустимий потік в мережі
— допустимий потік в мережі 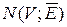 , то відповідний граф приростів
, то відповідний граф приростів 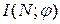 є орієнтованим графом, який має ті самі вершини, що мережа
є орієнтованим графом, який має ті самі вершини, що мережа  . Дуги цього графа визначаються наступним чином: для кожної дуги
. Дуги цього графа визначаються наступним чином: для кожної дуги 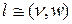 з
з  в графі
в графі 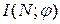 будується дуга
будується дуга 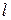 , якщо
, якщо  , а дуга
, а дуга 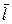 з оберненою орієнтацією
з оберненою орієнтацією  , якщо
, якщо  . Якщо в графі
. Якщо в графі 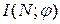 є дуга
є дуга 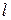 або
або 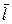 , то можна додати або відповідно відняти одиницю потоку в
, то можна додати або відповідно відняти одиницю потоку в 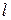 , не порушуючи допустимість потоку по цій дузі.
, не порушуючи допустимість потоку по цій дузі.
Нехай  — мережа з обмеженими пропускними здатностями. Тоді існують допустимі потоки з
— мережа з обмеженими пропускними здатностями. Тоді існують допустимі потоки з  у
у 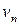 , які мають величину
, які мають величину  . Потрібно серед них вибрати такий, який мінімізує деяку кількісну міру, яку будемо називати вартістю.
. Потрібно серед них вибрати такий, який мінімізує деяку кількісну міру, яку будемо називати вартістю.
Припустимо, що 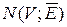 – задана мережа з обмеженнями
– задана мережа з обмеженнями  і
і  на пропускні здатності дуг. Нехай на ній задана функція
на пропускні здатності дуг. Нехай на ній задана функція  , яка приймає дійсні значення і кожній дузі
, яка приймає дійсні значення і кожній дузі  ставить у відповідність одиничну вартість
ставить у відповідність одиничну вартість  . Якщо
. Якщо 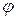 – довільний допустимий потік, то загальна вартість потоку
– довільний допустимий потік, то загальна вартість потоку 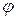 позначається
позначається 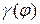 і визначається із співвідношення
і визначається із співвідношення  . Якщо
. Якщо  , то
, то  можна інтерпретувати як вартість переміщення одиниці потоку з
можна інтерпретувати як вартість переміщення одиниці потоку з  в
в 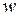 по дузі
по дузі 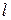 . Тоді
. Тоді 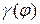 – сумарна вартість потоку в мережі.
– сумарна вартість потоку в мережі.
Важливо відзначити, що така модель застосовується для оцінки вартості потоків тільки тоді, коли вартість потоку в кожній дузі пропорційна величині потоку.
Розглянемо спочатку транспортні мережі (для них  ). Основна задача запишеться так: для заданої транспортної мережі
). Основна задача запишеться так: для заданої транспортної мережі  і функції вартості
і функції вартості  знайти допустимий потік
знайти допустимий потік 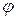 з
з  в
в 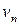 , величина якого рівна
, величина якого рівна  і вартість мінімальна.
і вартість мінімальна.
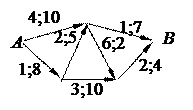 Для мережі
Для мережі
знайти допустимий потік мінімальної вартості. Перші цифри визначають вартість потоків на дугах, другі – пропускні здатності цих дуг.
Весь обчислювальний процес зображатимемо на рисунку 2.10.
Зліва показана необхідна послідовність графів приростів. Числа на дугах відповідають їх довжинам, дуги з нескінченними довжинами опущені, дуги, які входять в найкоротший шлях від джерела до стоку, виділені жирними лініями.
В правій частині малюнка зображена послідовність потоків мінімальної вартості в порядку зростання їх величини. Ці потоки одержані з допомогою послідовного додавання потоків на ланцюгах, які відповідають найкоротшим шляхам в графі приростів. Числа на дугах визначають величину потоку, який по них пропущений.
 |
| |

| 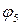
|

 | |||
 | |||

| |
|
|
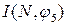
| 
|
 | |||
 | |||


|

| 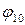
|

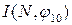
| 
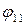
|
| Рис. 2.10. |
В загальному випадку знайдено чотири потоки на ланцюгах, які мають величини 5, 2, 3 і 1 відповідно. Кінцевий потік величиною 11 одиниць, очевидно буде максимальним, оскільки обидві дуги вже насичені.
Зауважимо, що перший граф приростів 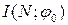 структурно ідентичний з вихідною мережею (тут
структурно ідентичний з вихідною мережею (тут  — потік тотожно рівний нулю по всіх дугах). Це пояснюється тим, що в даний момент ще немає насичених дуг і не існує додатних потоків, які б потенційно можна було б анулювати. У всіх наступних графах приростів деякі прямі дуги (зображаються суцільними лініями), які є насиченими, відсутні. Крім того, в них є деякі обернені дуги (пунктир), відповідні дугам, які мають додатний потік, що може бути виключений без порушення допустимості за рахунок використання дуги в оберненому напрямку.
— потік тотожно рівний нулю по всіх дугах). Це пояснюється тим, що в даний момент ще немає насичених дуг і не існує додатних потоків, які б потенційно можна було б анулювати. У всіх наступних графах приростів деякі прямі дуги (зображаються суцільними лініями), які є насиченими, відсутні. Крім того, в них є деякі обернені дуги (пунктир), відповідні дугам, які мають додатний потік, що може бути виключений без порушення допустимості за рахунок використання дуги в оберненому напрямку.
Простота наведеного прикладу дозволить візуально знайти найкоротші шляхи в кожному графі приростів. В більш складних випадках для знаходження кожного найкоротшого шляху необхідно використати інші методи, оскільки вибір найкоротшого шляху дасть в результаті потік, вартість якого не мінімальна. В цьому випадку його не можна використовувати за початкову точку при визначенні наступного приросту потоку.
В розглянутому прикладі кожний наступний граф приростів має тільки один найкоротший шлях. Проте це не завжди так. Коли є декілька найкоротших шляхів, будь-який з них можна використати в якості базису для знаходження наступного потоку по ланцюгу.
Слід зауважити, що хоча ми обійшлися без побудови потоків величини 1, 2, 3, 4, 6, 8 і 9 в розглянутому вище прикладі, такі потоки мінімальної вартості можна отримати. Наприклад, для одержання потоку мінімальної вартості величини 8 ми повинні додати до потоку  одну одиницю потоку по ланцюгу, який використовується для побудови
одну одиницю потоку по ланцюгу, який використовується для побудови 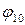 .
.
Контрольні запитання та задачі
1. Дайте визначення графа.
2. Які графи називаються скінченними, виродженими?
3. Які вершини називаються ізольованими, граничними точками ребра, суміжними?
4. Які ребра називають суміжними, паралельними?
5. Що називається петлею?
6. Які петлі називаються паралельними?
7. В чому різниця між суміжністю та інцидентністю?
8. Дайте визначення степеня вершини графа, маршруту.
9. Який маршрут називається замкнутим, ланцюгом, циклом?
10. Дайте визначення простого ланцюга, простого циклу.
11. Який граф називається повним?
12. Чому рівна степінь вершини повного графа?
13. Який граф називається доповненням графа?
14. Чому рівне число вершин повного графа?
15. Який граф називається зв’язним, незв’язним, деревом, лісом?
16. Який граф називають підграфом графа 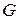 ?
?
17. Яке ребро графа називається мостом?
18. В якому випадку дерево покриває граф?
19. Яке ребро називається орієнтованим?
20. Який граф називається орієнтованим?
21. Дайте визначення степеня виходу і степеня входу вершини А.
22. Яка вершина орієнтованого графа називається вершиною-джерелом, вершиною-стоком?
23. Дайте визначення шляху в орієнтованому графі.
24. Який шлях в орієнтованому графі називається простим, замкнутим, орієнтованим циклом?
25. В якому випадку кажуть, що вершина В досяжна з вершини А?
26. Що розуміють під довжиною шляху?
27. Що називають відстанню між двома вершинами?
28. Дайте визначення матриці суміжності, інцидентності, шляхів.
29. Які графи називають мережами?
30. Що представляє собою задача мінімізації мережі?
31. В чому суть задачі про найкоротший шлях?
32. Дайте визначення потоку в мережі, чистого потоку.
33. Як класифікують мережі за впливом на потік?
34. Які два потоки  і
і  називають узгодженими?
називають узгодженими?
35. Яка дуга називається протилежною?
36. Дайте визначення мережі з пропускною здатністю, допустимого потоку, графу, приростів.
37. Як визначається загальна вартість потоку?
38. Дайте визначення джерела, стоку і проміжної вершини для мережі.
39.  Для графа
Для графа
дайте відповіді:
а) які точки є граничними для кожного з ребер; б) для кожного ребра вкажіть суміжні з ним; в) для кожної вершини вкажіть суміжні з нею і її степінь.
40. Намалюйте повний граф з 5 і 7 вершинами.
41. Чи існує повний граф з 5, 7, 10, 15 ребрами? Якщо існує, то скільки кожен з них має вершин?
42. Намалюйте графи, які є доповненням до графів
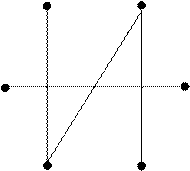 | |||||
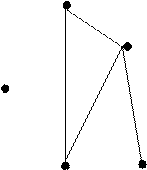 | |||||
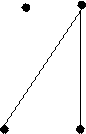 | |||||
43. Нехай граф 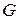 має чотири вершини, А — одна з них,
має чотири вершини, А — одна з них,  — його доповнення. Скільком ребрам належить вершина А в графі
— його доповнення. Скільком ребрам належить вершина А в графі  , якщо в графі
, якщо в графі 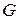 вона належить одному, трьом і жодному ребру.
вона належить одному, трьом і жодному ребру.
44. Намалюйте граф з 5 вершинами, в якого: а) одна вершина ізольована, а друга степеня 4; б) рівно дві вершини мають однаковий степінь; в) степені всіх вершин різні між собою.
45.  Для графа
Для графа
вказати всі маршрути, шляхи, прості шляхи.
46.  В графі
В графі
вкажіть цикли, які містять 4, 5, 6, 10 ребер, прості цикли.
47. Нарисуйте граф з п’ятьма вершинами, який не є зв’язним.
48. Вкажіть всі мости графа
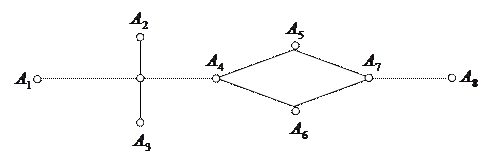 |
49. Які ребра треба видалити в графі,
 |
щоб він став деревом.
50. Для графа побудувати всі покриваючі дерева
 |
|
|
|
|
51. 


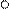 В графі
В графі
 |
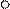 визначити: а) степінь входу і виходу кожної вершини; б) джерело і стік; в) число шляхів від
визначити: а) степінь входу і виходу кожної вершини; б) джерело і стік; в) число шляхів від  до
до  ; г) назвіть вершину, яка недосяжна з жодної вершини.
; г) назвіть вершину, яка недосяжна з жодної вершини.
52.  В графі
В графі
 | |||
 | |||
підрахувати кількість шляхів. Визначити відстань від  до
до  , від
, від  до
до  , від
, від  до
до  .
.
53. Побудувати графи за даними матрицями суміжності
а) б)
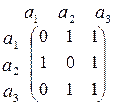

54. Побудувати графи за даними матрицями інцидентності
а) б)
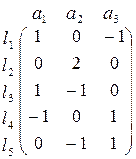
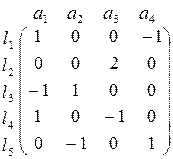
Читайте також:
- АВТОМАТИЧНА КОМУТАЦІЯ В МЕРЕЖАХ ЕЛЕКТРОЗВ'ЯЗКУ
- Адресація в IP-мережах
- Вантажопотоки
- Вантажопотоки, їх види та формування.
- Вибір перерізу провідників у мережах напругою до 1000 В з урахуванням плавких запобіжників
- Вибір перерізу провідників у мережах напругою до 1000В з урахуванням автоматичних вимикачів і теплових реле
- Види звітів про грошові потоки.
- Внутрішнім джерелом фінансування є накопичені нетто-грошові потоки, що виникають при здійсненні міжнародних операцій.
- ГРОШОВИЙ ОБОРОТ ТА ГРОШОВІ ПОТОКИ
- Грошові потоки як об’єкт фінансового менеджменту
- Документні потоки в установі
- Електричних мережах.
| <== попередня сторінка | | | наступна сторінка ==> |
| Задача про найкоротший шлях | | | РОЗДІЛ 3. ЕЛЕМЕНТИ ТЕОРІЇ ІГОР |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |