• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Задача нелінійного програмування

Лінійні моделі є ефективним засобом дослідження широкого кола задач управління та економіки. Виникнення НП пов’язане з тим, що припущення про лінійну залежність можуть лише наближено характеризувати об’єкт дослідження. В більшості випадків залежність між основними параметрами системи є нелінійною.

Наприклад, дохід від реалізації продукції є нелінійною функцією ціни: чим нижча ціна тим більший попит і, відповідно, більший обсяг реалізації. Закон спадаючої ефективності виробництва свідчить про нелінійну залежність обсягів виробництва від собівартості продукції. Різного виду затрати праці та матеріальних ресурсів, як правило, є нелінійними функціями точності, надійності та інших характеристик якості продукції виробництва.

В зв’язку з вищесказаним, виникає потреба у використанні нелінійних моделей як більш узгоджених з практикою.

НП охоплює широкий клас настільки складних задач, що досі не розроблені загальні методи, подібні СМ в ЛП, які б дозволяли розв’язувати будь-які ЗНП. Проблеми розв’язування нелінійних задач на відміну від ЗЛП, полягають перш за все в тому, що область допустимих розв’язків в них може бути неопуклою або мати нескінченне число кутових точок, або і перше і друге одночасно. При нелінійності цільової функції виникають і інші труднощі: оптимум може досягатися не тільки на границі, але і в середині допустимої області; цільова функція може мати в допустимій області декілька локальних екстремумів.

В загальному вигляді ЗНП формулюється так: знайти вектор , який задовольняє системі обмежень

(4.13)

і забезпечує екстремум функції . (4.14)

При цьому вважають, що функці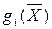ї і відомі. Як і для ЗЛП, на всі або частину змінних задачі накладаються умови невід’ємності.. Крім цього, обмеженням може бути умова цілочисельності розв’язку для деяких або всіх змінних.

Якщо , , ,де – відомі сталі, то при умові невід’ємності розв’язків отримаємо ЗЛП.

В залежності від виду системи обмежень і цільової функції ЗНП діляться на задачі:

– дробово-лінійного програмування (ДЛП) – коли цільова функція раціональна, а система обмежень задається системою лінійних рівнянь і нерівностей;

– опуклого програмування – коли цільова функція та обмеження відповідно опуклі функції та опуклі області;

– квадратичного програмування – коли цільова функція квадратична, обмеження є системою лінійних рівнянь і нерівностей.

Читайте також:

1. Алгебраїчне та інсерційне програмування
2. Безпосереднє програмування відеопам'яті
3. Взаємне положення площин. Перша позиційна задача
4. Взаємне положення прямої і площини. Друга позиційна задача.
5. Виконання програми - реалізація мови програмування
6. Використання пакету Maple для розв’язування задач лінійного програмування
7. Вступ до мови програмування
8. Вторая задача анализа на чувствительность
9. Геометрична інтерпретація задачі лінійного програмування
10. Геометрична інтерпретація задачі нелінійного програмування
11. Геометрична інтерпретація розв’язків цілочислових задач лінійного програмування на площині
12. Графічний метод розв’язування задач лінійного програмування

Переглядів: 1400