• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Рівнем ризику

Введемо позначення:

тривалість циклу замовлення;

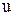– термін виконання замовлення, тобто час від моменту подачі замовлення до його поставки;

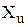– випадкова величина, яка є величиною попиту протягом терміна виконання замовлення;

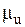– середня величина попиту протягом терміна виконання замовлення;

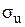– середнє квадратичне відхилення величини попиту протягом терміна виконання замовлення;

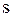– розмір резервного запасу;

максимально можливе значення ймовірності вичерпання запасу протягом терміна виконання замовлення (рівень ризику дефіциту);

витрати на постачання однієї партії товару на поповнення запасу;

витрати зберігання одиниці запасу протягом періоду.

Знайдемо спочатку оптимальний розмір поповнення запасу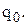

Функція витрат на поповнення і зберігання запасів вобсягі одиниць з урахуванням величини резервного запасу 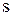має вигляд:

(3.1)

Оптимальний розмір поповнення запасу 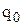визначаємо із умови 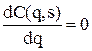, яка дає .

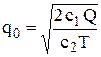У дійсності поповнення запасу може відбуватись не миттєво в момент подачі замовлення, а з деяким терміном. Для більшості реальних ситуацій існує додатний термін виконання замовлення u (часове запізнення) від моменту його подачі до реальної поставки. Щоб зменшити ймовірність дефіциту, необхідно створювати резервні запаси. У цьому випадку замовлення потрібно подавати, коли середній попит за час поставки перевищить наявні запаси, тобто коли рівень наявного запасу опуститься до точки одиниць, де резервний запас.

На рис. 3.1 показана залежність між розміром резервного запасу 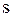і параметрами стохастичної моделі економічного розміру замовлення, яка включає термін виконання замовлення 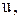середню величину попиту 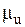, економічний розмір замовлення 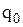і тривалість циклу .

Рис. 3.1

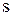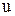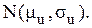Визначимо рівень резервного запасу у випадку, коли дефіцит запасу у системі недопустимий. Основним припущенням при побудові моделі є те, що величина попиту протягом терміну виконання замовлення є нормально розподіленою випадковою величиною із середнім значенням і середнім квадратичним відхиленням , тобто має розподіл Задача полягає у знаходженні такого значення щоб при заданому коефіцієнті ризику імовірність дефіциту дорівнювала

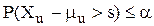, або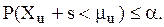

Для випадку нормального розподілу щільність імовірності дорівнює

Перетворенням приводимо нормальний розподіл з довільними параметрами 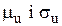до стандартного розподілу з 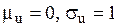і щільністю

Для знаходження 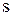необхідно розв’язати рівняння

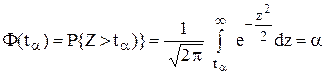
відносно де

Величина називається квантилем розподілу 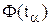. У Mathcad 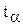визначається як квантиль нормованого нормального розподілу 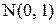із середнім 0 і стандартним відхиленням 1 за оператором , де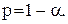

Коефіцієнт характеризує важливий показник політики фіксованого ризику, виражений процентним відношенням числа дефіцитних циклів до загального числа циклів замовлень 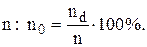Отже, 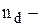число випадків, коли рівень запасів зменшується до нуля, а чергова партія у ці моменти ще не надійшла. Якщо величина Х має нормальний розподіл, то для середнє значення складе 17, 2,5 і 0,5%.

За знайденим значенням визначаємо обсяг резервного запасу 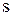і точку замовлення :

(3.2)

Величина попиту протягом терміна виконання замовлення 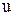описується щільністю розподілу ймовірностей, віднесеною до одиниці часу (наприклад, до тижня або місяця). Якщо попит за одиницю часу є нормально розподіленою випадковою величиною із середнім 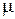і стандартним відхиленням 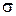, то загальний попит протягом терміна виконання замовлення 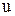буде мати розподіл 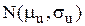з параметрами і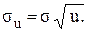

На рис 3.1. представлена зміна рівня запасу у часі у припущенні, що термін виконання замовлення u менше тривалості циклу замовлення , що у загальному випадку виконується не завжди. У протилежному випадку визначається ефективний термін виконання замовлення у вигляді

,

де m – найбільше ціле, яке не перевищує 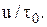Таке рішення виправдовується тим, що після m циклів (кожний довжиною 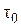) ситуація управління запасами стає такою ж, як і у випадку, якщо б інтервал між подачею одного замовлення і одержанням другого дорівнював .

Коментар. Оптимальна стратегія управління запасами для моделі без дефіциту з фіксованим рівнем ризику дефіциту має такі параметри: оптимальний розмір поповнення запасу дорівнює одиниць продукції, оптимальний резервний запас – 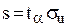, точка замовлення на поповнення запасу одиниць.

Приклад 3.1. Загальний об’єм замовлень товару, який здійснюється торгівельною фірмою за період T=365 днів дорівнює Q=3650 одиниць. Товари постачаються партіями однакового об’єму, вказаному у замовленні. Витрати на постачання однієї партії складають 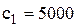грн., витрати на зберігання одиниці запасу за добу дорівнюють 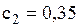грош. од. Дефіцит товару недопустимий. Термін виконання замовлення від моменту його подачі до реальної поставки складає днів.

Для детермінованої моделі системи управління запасами (приклад 2.1) оптимальною є така стратегія: обсяг замовлень одиниць, середня кількість замовлень у рік 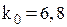разів, інтервал часу між замовленнями 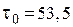днів.

Визначимо ці ж параметри, а також величину резервного запасу 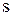і точку замовлення 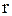для стохастичної моделі таким чином, щоб імовірність вичерпання запасу (імовірність дефіциту) не перевищувала при умові, що денний попит є нормально розподіленою випадковою величиною з математичнім сподіванням 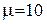одиниць у день і середнім квадратичним відхиленням одиниці, тобто має розподіл .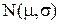

Читайте також:

1. Абстрактна небезпека і концепція допустимого ризику.
2. Акустичні рівнеміри
3. Аналiз ризику методами iмiтацiйного моделювання
4. Аналіз втрат від маркетингового ризику
5. Аналіз кредитного ризику банку
6. Аналіз невизначеності і ризику
7. Аналіз ризику в життєдіяльності людини.
8. Аналіз ризику можливих збитків
9. Аналіз ризику через моделювання.
10. Аналіз та оцінка інвестування в умовах ризику. Якісні та кількісні методи оцінювання проектних ризиків.
11. Взаємодія важелів. Оцінка сукупного ризику, зв'язаного з підприємством.
12. Взаємозалежність між рівнем соціально-економічного розвитку суспільства і державно-правовими інститутами.

Переглядів: 619