
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 9. Принципи побудови економетричних моделей. Парнолінійна регресія
Між економічними показниками часто існує кількісний взаємозв’язок, який оцінюється за допомогою економетричних моделей. Потім на їх основі визначаються наявні тенденції та складаються прогнози.
Показник, який впливає на інший, позначається змінною х (пояснювальна, результуюча, незалежна змінна). Змінна y(результативна, залежна) позначає показник, який зазнає впливу.
У загальному вигляді економетрична модель виглядає наступним чином:

де X — пояснювальні змінні (x1, x2, xn); u — випадкова (стохастична), складова, яку називають залишком, помилкою, відхиленням або збуренням.
Якщо у економетричній моделі пояснювальна змінна одна, регресія є парною, а якщо дві чи більше – множинною, або багатофакторною.
Побудова економетричних моделей містить певні труднощі. По-перше, потрібно вибрати вірний вид регресії (лінійна, степенева, логарифмічна тощо). По-друге, при оцінці параметрів моделей часто існують такі небажані явища, як мультиколінеарність (тісний зв’язок між пояснювальними змінними), гетероскедастичність (непостійна дисперсія залишків для різних спостережень), автокореляція (зв’язок між залишками через певний проміжок часу). Ігнорування важливої пояснювальної змінної або врахування зайвої змінної призводять до зміщення оцінок параметрів. Зазначені явища не дозволяють оцінювати параметри моделі методом найменших квадратів, тому її потрібно додатково коректувати.
Теоретичні значення змінних у економетричній моделі повинні бути якомога ближче до фактичних значень. Однак, відхилення можуть бути як позитивні, так і негативні, тому потрібно мінімізувати суму їх квадратів. На цьому базується метод найменших квадратів (1 МНК). Згідно нього, параметри моделі можна знайти, розв’язавши систему рівнянь, яка для лінійної залежності виглядатиме наступним чином:

Для параболічної та гіперболічної залежностей потрібно в зазначеній системі замінити х відповідно на х2 та 1/х.
Приклад 9.1
Побудувати економетричну модель залежності витрат матеріалу на одиницю продукції від обсягу випуску продукції.
| Номер підприємства | |||||||
| Випуск продукції, тис. шт. | 1,0 | 0,5 | 0,7 | 0,3 | 0,25 | 0,34 | 0,13 |
| Витрати матеріалу на одиницю продукції, тис. грн. | 1,5 | 1,6 | 2,7 | 5,0 | 4,5 | 2,5 | 5,0 |
Розв’язання
Нехай шукана залежність описується прямою лінією
Y = a0+ a1X + u,
де Y — витрати матеріалу на одиницю продукції; X — випуск продукції, тис. грн.
Складемо таблицю для розрахунку параметрів моделі методом найменших квадратів (табл. 9.1):
Таблиця 9.1
Застосування методу найменших квадратів для парної лінійної регресії
| № | x | y | x2 | y2 | x * y | і | u2 | 
| 
|
| 1,5 | 2,25 | 1,5 | 1,1 | 0,16 | 3,09 | 4,65 | |||
| 0,5 | 1,6 | 0,25 | 2,56 | 0,8 | 3,1 | 2,24 | 2,75 | 0,02 | |
| 0,7 | 2,7 | 0,49 | 7,29 | 1,89 | 2,3 | 0,16 | 0,31 | 0,92 | |
| 0,3 | 0,09 | 2,5 | 1,5 | 3,9 | 1,22 | 3,04 | 0,41 | ||
| 0,25 | 4,5 | 0,0625 | 20,25 | 1,13 | 4,1 | 0,16 | 1,54 | 0,71 | |
| 0,34 | 2,5 | 0,12 | 6,25 | 0,85 | 3,74 | 1,53 | 0,57 | 0,23 | |
| 0,13 | 0,0169 | 0,65 | 4,58 | 0,18 | 3,04 | 1,75 | |||
| Σ | 3,22 | 22,8 | 2,03 | 88,6 | 8,32 | 22,8 | 5,65 | 14,34 | 8,7 |
Для наших даних система рівнянь має вигляд

З першого рівняння виражаємо  і підставляємо в друге.
і підставляємо в друге.
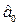 = 5,1;
= 5,1; 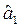 = -4.
= -4.
Таким чином, економетрична модель має вигляд
Y = 5,1 – 4X + u.
Оскільки 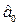 = 5,1 ¹ 0, то рівень витрат матеріалу на одиницю продукції не строго пропорційний до обсягу випуску продукції. Значення
= 5,1 ¹ 0, то рівень витрат матеріалу на одиницю продукції не строго пропорційний до обсягу випуску продукції. Значення 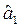 = -4 означає, що збільшення випуску продукції на 1 тис. шт. веде до зменшення витрат матеріалу на одиницю продукції гранично на 4 тис. грн.
= -4 означає, що збільшення випуску продукції на 1 тис. шт. веде до зменшення витрат матеріалу на одиницю продукції гранично на 4 тис. грн.
Коефіцієнт еластичності знаходимо за формулою:
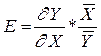

Отже, при збільшенні випуску продукції на 1% витрати матеріалу на одиницю гранично зменшаться на 0,56%.
Тісноту зв’язку між змінними у моделі оцінимо за допомогою коефіцієнту детермінації (R2) та коефіцієнту кореляції (R).


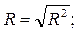

Зміна витрати матеріалу на одиницю продукції на 61% пояснюється зміною обсягів випуску продукції, а на 39% – іншими чинниками.
Питання для самостійного вивчення: t-критерій Стьюдента, F-критерій Фішера.
Читайте також:
- Аграрна політика як складова економічної політики держави. Сутність і принципи аграрної політики
- Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
- Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
- Алгоритм побудови калібрувального графіка для визначення загального білка сироватки крові
- Алгоритм побудови організаційних структур управління.
- Алгоритм побудови сітьових графіків.
- Алгоритми побудови дерев екстремальної ваги
- Антикорупційні принципи
- Антикорупційні принципи
- Антикорупційні принципи
- Антикорупційні принципи
- АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 8. Система показників кількісного оцінювання ступеня ризику | | | Тема 10. Лінійні моделі множинної регресії |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |