
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Малюнок 11.3.
Формування умінь учнів розв'язувати складені задачі розпочинається після введення першої складеної текстової задачі і продовжується протягом всього періоду вивчення математики у початкових класах. Аналіз досліджень, які розглядають різноманітні аспекти навчання школярів розв'язувати текстові задачі (роботи М.В.Богдановича, Ю.М.Колягіна, А.А.Свєчнікова, Л.М.Скаткіна, Л.М.Фрідмана та ін.), дозволяють виявити структуру цього складного уміння. Загальне уміння розв’язувати задачі є складним умінням, оволодіння яким передбачає сформованість певних часткових умінь. Структурними компонентами загального уміння розв’язувати задачі є наступні часткові уміння: 1) уміння прочитати задачі, ставлячи відповідні логічні наголоси на даних задачі, на зв’язку між даними і невідомим, виділення наголосом запитання задачі; 2) уміння записати задачу коротко, коли цього вимагає вчитель; 3) уміння скласти за задачею опорну схему або модель задачі; 4) уміння проаналізувати задачу; 5) уміння скласти план розв’язання задачі; 6) уміння записати розв’язання задачі відповідно до вимог вчителя; 7) уміння працювати над розв’язаною задачею (уміння виконати перевірку розв’язання задачі, уміння скласти обернену задачу, уміння видозмінити задачу тощо).
Проаналізувавши методичні посібники для вчителів, наявні підручники з математики для початкових класів, можна встановити, що для формування вказаних умінь використовується система вправ. Вона включає до свого складу принаймні наступні завдання: 1) розв’язування задач різних типів і видів; 2) вправи, основне призначення яких полягає в тому, щоб ознайомити дітей із загальними правилами роботи над задачею. Вивчення досвіду роботи вчителів свідчить, що вони з цією метою використовують різноманітні пам’ятки, одна з яких представлена у таблиці № 11.9. Спочатку така пам’ятка може висіти в класі, а потім її потрібно зняти, дозволивши користуватися нею лише тим дітям, які без неї не можуть самостійно розв’язати вказану задачу. 3) повторне розв'язування тих самих задач через певний проміжок часу; 4) завдання, в яких потрібно у розв’язаній задачі змінити числові дані чи шукану величину (наприклад: заміни кількість білих кролів; заміни число 9 іншим; заміни шукане тощо); 5) завдання, в яких запитання слід замінити таким новим, для якого задається нове запитання або вказується, які зміни необхідно внести до запитання; 6) вправи, в яких після розв’язання задачі пропонується змінити сюжет задачі, зберігши задані числа (можливо відповідно до індивідуальних особливостей школярів з метою особистісної орієнтації навчального процесу задати новий сюжет чи дозволити обрати його довільно); 7) завдання, в яких учням пропонується замінити наявні у даній задачі зв’язки замінити іншими, коли вони вказані чи не вказані; 8) вправи, в яких перед учнями ставиться завдання на поступове ускладнення задачі завдяки збільшенню числових даних у задачі або включенню нових зв’язків між даними. (приклад такого ускладнення представлено у таблиці № 11.10.); 9) розв’язування задач різними способами; 10) вправи, в яких після розв’язання задачі пропонується скласти вираз, пояснивши, що означає кожне число чи вираз; 11) завдання на складання задач, які можуть бути принаймні наступних видів: а) на зазначену дію; б) за поданим розв’язанням; в) за заданим виразом чи рівнянням; г) із вказаною залежністю між величинами; д) із вказівкою на вид чи тип задачі; е) на складання обернених задач; є) за числовими даними; ж) за малюнком; з) за схемою тощо; 12) вправи на порівняння задач; 13) завдання на складання плану розв’язання задачі; 14) вправи, в яких потрібно провести аналіз задачі; 15) завдання, в яких слід розв’язати задачі за поданим планом.
Таблиця № 11.9. Пам’ятка “Як працювати над задачею”.
| 1. Уважно прочитай задачу! 2. З «ясуй незрозумілі слова! 3. Виділи умову задачі! 4. Уважно прочитай запитання і поміркуй, що слід знати, щоб дати відповідь на нього! 5. Подумай, що означає кожне число в задачі! 6. Який існує зв’язок між даними задачі? 7. Як пов’язані між собою дані та шукане? 8. Проаналізуй задачу! 9. Наміть план розв'язування! 10. Якщо план намітити не вдалося, то зроби короткий запис умови задачі! 11. Чи можна тепер дати відповідь на запитання задачі? 12. Оформи розв’язання задачі вказаним способом! 13. Перевір відповідь задачі! 14. Подумай, чи є інші способи розв’язання задачі! |
Проведені дослідження свідчать, що розв'язування складених задач займає досить багато часу уроку, але разом з тим значна частина дітей продовжує відчувати значні труднощі при виборі та обґрунтуванні відповідної арифметичної дії, при самостійному розв’язуванні задач. Для таких школярів, як засвідчили результати експериментального навчання, доцільно з метою формування вказаних умінь використовувати усні вправи у вигляді завдань-запитань, спрямованих на навчання дітей вибору потрібної арифметичної дії, на порівняння задач, що містять схожі формулювання, на самостійну роботу з розв'язування складених задач без попереднього розбору їх з вчителем. Використання тих чи інших видів вказаних вправ повинне обумовлюватися індивідуально-психологічними особливостями дітей. Такий підхід, з одного боку, сприятиме особистісній зорієнтованості навчального процесу, а з іншого – дозволить економити час уроку.
Таблиця № 11.10. Ускладнення задач.
| Задачі | Вказівки на вид ускладнень |
| Турист за день пройшов 10 км пішки та проїхав 240 км на автомобілі. Яку відстань подолав турист за день? | Зміни задачу так, щоб було задано швидкість і час руху пішки! |
| Турист йшов 2 год зі швидкістю 5 км/год і проїхав 240 км на автомобілі. Яку відстань подолав турист за день? | Зміни задачу так, щоб було задано швидкість і час руху пішки та автомобілем! |
| Турист йшов 2 год зі швидкістю 5 км/год та їхав автомобілем 4 години із швидкістю 60 км/год. Яку відстань подолав турист за день? | Зміни задачу так, щоб було невідомо час руху автомобілем! |
| Турист пішки йшов 2 години зі швидкістю 5 км/год, а їхав на автомобілі на 2 години більше зі швидкістю 60 км/год. Яку відстань подолав турист за день? |
Спостереження за роботою вчителів дають підстави для висновку про те, що досить часто вчителі використовують лише один з можливих двох способів аналізу задачі: чи аналітичний (від запитання до умови), чи синтетичний (від умови до запитання). Проведені методистами дослідження переконливо доводять, що жоден з них не можна вважати універсальним. Крім того, універсалізація може нанести лише шкоду. Для того, щоб навчання умінню відшукати шлях розв’язання складеної задачі було особистісно-зорієнтованим, слід відповідно до індивідуальних особливостей дітей використовувати підготовчі завдання такого виду: 1) що можна визначити за цими даними? (у процесі їхнього виконання діти приходять до таких висновків: не все, що можна знайти за вказаними даними, потрібно визначати, щоб розв’язати задачу; виконувати слід лише ті дії, результати яких використовуються для одержання відповіді на запитання задачі); 2) що показують наступні вирази?; 3) виконай аналіз задачі двома способами, вказавши переваги чи недоліки кожного з них; 4) коли будеш шукати спосіб розв’язання задачі, міркуй від запитання до умови (або навпаки); 5) завдання на складання плану розв’язання задачі без наступного її розв'язування.
Вивчення продуктів діяльності учнів яскраво свідчить, що досить часто їм досить важко відрізнити просту задачу від складеної. Якщо дитина не може зробити цього, то відповідно до індивідуальних особливостей корисно у період ознайомлення учнів зі складеними задачами та формування умінь їх розв'язувати розглядати складені задачі у протиставленні та зіставленні з простими, З цією ж метою дуже корисно використовувати завдання на перетворення простих задач у складені та навпаки. Експериментальні дослідження свідчать, що такий підхід буде сприяти формуванню уявлень учнів про складену задачу та процес її розв'язування, а також формуватиме уміння розв'язувати складені текстові задачі. Так, при розв’язуванні складених задач виду “В одному куску 7 м тканини, а в другому на 3 м більше. Скільки метрів тканини в обох кусках разом?” учні обмежуються однією дією 7+3=10, вважаючи, що задачу розв’язано. Причинами подібних помилок є зовнішня схожість структур простої та складеної задач. Для того, щоб попередити такі помилки та забезпечити особистісно-зорієнтований підхід до навчання школярів розв'язувати задачі, слід відповідно до індивідуальних потреб дітей пропонувати їм завдання, представлені у варіантах №№ 1 і 2 таблиці № 11.11. Для учнів, які спроможні самостійно справитися з розв’язанням таких задач, слід пропонувати завдання, спрямовані на регулювання процесу розв’язання або на перетворення задачі (такі завдання представлені у варіантах №№ 3 і 4 таблиці № 11.11.).
Таблиця № 11.11.
| І варіант | ІІ варіант |
 1. Закінчи короткий запис задачі: 1. Закінчи короткий запис задачі:
  І кусок – ÿ
? І кусок – ÿ
?
 ІІ кусок - ? на 3 м більше, ніж
2. Запиши вираз для відповіді на запитання: “Скільки метрів тканини у другому куску?”
3. Використовуючи схему, закінчи розв’язання задачі:
(7 + ÿ) + ÿ = ÿ
4. Запиши відповідь. ІІ кусок - ? на 3 м більше, ніж
2. Запиши вираз для відповіді на запитання: “Скільки метрів тканини у другому куску?”
3. Використовуючи схему, закінчи розв’язання задачі:
(7 + ÿ) + ÿ = ÿ
4. Запиши відповідь.
| 1. Закінчи короткий запис задачі:
   І кусок –
? І кусок –
?
 ІІ кусок - ? на ÿ більше, ніж
2. Використовуючи схему, склади за задачею вираз та обчисли його значення:
(ÿ + ÿ) + 7 =
3. Запиши відповідь. ІІ кусок - ? на ÿ більше, ніж
2. Використовуючи схему, склади за задачею вираз та обчисли його значення:
(ÿ + ÿ) + 7 =
3. Запиши відповідь.
|
| ІІІ варіант | ІУ варіант |
| 1. Використовуючи опорні слова, зроби короткий запис задачі: І кусок – . . . . . . ІІ кусок - . . . 2. Розв’яжи задачу, склавши за нею вираз. 3. Запиши відповідь. | 1. Зроби короткий запис задачі. 2. Розв’яжи задачу та запиши відповідь. 3. Заміни в умові слово “більше” словом “менше”. 4. Запиши розв’язання одержаної задачі. |
Спостереження за роботою вчителів свідчать, що певна їх частина при повторенні пройденого мало використовує завдань творчого характеру. Такий підхід не сприяє особистісній орієнтації навчального процесу та гальмує розвиток сильних учнів. ТМО особистісно-зорієнтованого навчання вимагають дотримання такої закономірності: питома вага завдань творчого характеру під час повторення пройденого повинна неухильно зростати. Покажемо, як це можна зробити при навчанні учнів розв'язувати складені задачі, на прикладі такої задачі “Крісло коштує 200 гривень, а диван на 380 гривень дорожчий. Скільки коштують разом крісло та диван?”. Відповідні можливі варіанти роботи представлені у таблиці № 11.12.
Таблиця № 11.12.
| І варіант | ІІ варіант |
 1. Закінчи короткий запис задачі:
К. - . . .
?
Д. - ? на ÿ дорожчий
2. Використовуючи схему, запиши розв’язання задачі:
( ÿ + ÿ ) + ÿ =
3, Запиши відповідь.
4. Запиши слово, яким можна замінити слово дорожчий. 1. Закінчи короткий запис задачі:
К. - . . .
?
Д. - ? на ÿ дорожчий
2. Використовуючи схему, запиши розв’язання задачі:
( ÿ + ÿ ) + ÿ =
3, Запиши відповідь.
4. Запиши слово, яким можна замінити слово дорожчий.
| 1. Користуючись опорними словами, зроби короткий запис задачі:
 К. - . . .
?
Д. -
2. Розв’яжи задачу.
3. Запиши відповідь.
4. Запиши на скільки гривень крісло дешевше, ніж диван – на ÿ грн. К. - . . .
?
Д. -
2. Розв’яжи задачу.
3. Запиши відповідь.
4. Запиши на скільки гривень крісло дешевше, ніж диван – на ÿ грн.
|
| ІІІ варіант | ІУ варіант |
| 1. Розв’яжи задачу, склавши за нею вираз. 2. Запиши відповідь. 3. Склади короткий запис задачі за даним розв’язанням: 200+380=580 (грн) | 1. Розв’яжи задачу та запиши відповідь. 2. Склади короткий запис задачі за даним розв’язанням: 580–200=380 (грн) |
При розв’язуванні задачі “Вранці в море вийшло 20 маленьких та 8 великих рибальських човнів. 6 човнів повернулися. Скільки човнів з рибалками повинні ще повернутися?” можна запропонувати такі варіанти особистісно-зорієнтованих завдань відповідно до індивідуальних особливостей школярів (див. таблицю № 11.13.).
Таблиця № 11.13.
| І варіант | ІІ варіант |
| 1. Закінчи короткий запис задачі: Вийшли – 20 ч. і 8 ч. Повернулися - ÿ Повинні повернутися - ? 2. Склади вираз для відповіді на запитання “Скільки всього човнів вийшло в море?” 3. Використовуючи схему, запиши розв’язання задачі: ( ÿ + ÿ ) - ÿ = ÿ 4. Запиши відповідь. | 1. Закінчи короткий запис задачі: Вийшли – 20 ч. і ÿ Повернулися - ÿ Повинні повернутися - . . . 2. Використовуючи схему, запиши розв’язання задачі: ( 20 + ÿ ) * ÿ = ÿ 3. Запиши відповідь. |
| ІІІ варіант | ІУ варіант |
| 1. Зроби короткий запис задачі: Вийшли – ÿ і ÿ Повернулися - ÿ Повинні повернутися - ? 2. Розв’яжи задачу, склавши за нею вираз. 3. Запиши відповідь. 4. Запиши розв’язання цієї задачі, якщо відомо, що повернулося 6 великих човнів. | 1. Розв’яжи задачу та запиши відповідь. 2. Запиши розв’язання цієї задачі, якщо відомо, що повернулося 6 маленьких човнів 3. Запиши розв’язання цієї задачі, якщо відомо, що повернулося 4 великих та 2 малих човни. |
Для задачі “У Зої було 6 зошитів у клітинку та 4 зошити у лінійку. 2 зошити у клітинку вона віддала братові. Скільки зошитів залишилося у Зої?” можна запропонувати такі варіанти особистісно-зорієнтованих завдань (див. таблицю № 11.14.).
Таблиця № 11.14.
| І варіант | ІІ варіант |
| 1. Закінчи короткий запис умови задачі: Було - 6 зошитів в кл. і 4 зошита в л. Віддала – Залишилось – 2. Використовуючи коротку схему, запиши розв’язання задачі: ( ÿ + ÿ ) * ÿ = ÿ 3. Запиши відповідь. | 1. Закінчи короткий запис умови задачі: Було - 6 зошитів в кл. і ÿ зошита в л. Віддала – Залишилось – 2. Використовуючи схему, запиши розв’язання задачі: ( ÿ * ÿ ) * ÿ = ÿ 3. Запиши відповідь. |
| ІІІ варіант | ІУ варіант |
| 1. Розв’яжи задачу, склавши за нею вираз. 2. Запиши відповідь. 3. Запиши числом, скільки зошитів у клітинку залишиться у Зої, якщо вона віддасть брату ще 3 зошити у лінійку. | 1. Склади за задачею вираз та обчисли його значення. 2. Запиши відповідь. 3. Запиши, які зміни потрібно внести в умову задачі, щоб її можна було розв’язати трьома способами. |
У відповідності з індивідуально-психологічними особливостями учнів для формування умінь розв'язувати складені задачі можна запропонувати такі особистісно-зорієнтовані завдання: 1) змініть умову задачі “У Миколки було 15 копійок. Він витратив на сніданок 10 копійок, а потім татко дав йому ще 20 копійок. Скільки грошей залишилося у Миколки?” так, щоб вона розв’язувалася таким виразом: а) (15-10)+20; б) (15+10)+20; в) (15+10)–20 (використання таких вправ не вимагатиме від вчителя додаткових затрат часу при підготовці до уроку та на перевірку результатів виконаної роботи. Крім того, застосування вказаних завдань сприятиме розвиткові школярів.); 2) якою повинна бути умова задачі, щоб її розв’язання було таким (7-3)+5?; 3) придумати задачу за таким виразом (6+4)+4; 4) розв’яжи задачу “За 3 книжки Петрик заплатив 90 копійок. Перша книжка коштувала 32 копійок, а друга 28 копійок. Скільки коштувала третя книжка?” таким способом, щоб: а) першою дією було додавання, а другою – віднімання; б) щоб обидві дії були відніманням; в) при розв’язанні довелося складати такий вираз (90–(32+28); г) при розв’язанні довелося складати такий вираз (90-32)-28. Враховуючи індивідуальні особливості та можливості учнів до розв'язування задач, можна пропонувати їм картки, на яких є допоміжний елемент, що полегшує виконання основного завдання чи додаткове завдання для сильних учнів. Такі вправи представлені у таблиці № 11.15.
Таблиця № 11.15.
| Картка 1. | Картка 2. | Картка 3. | Картка 4. |
| Розв’яжи задачу № 672 (ІІ клас) двома способами: 1-й спосіб: спочатку визнач, скільки суконь зшила кожна швачка окремо, а потім дай відповідь на запитання задачі. 2-й спосіб: спочатку визнач, скільки метрів тканини було у двох швачок разом, а потім дай відповідь на запитання задачі. | Розв’яжи задачу № 730 двома способами: 1-й спосіб: (ÿ+ÿ)·ÿ. 2-й спосіб: ÿ·ÿ+ÿ·ÿ. Поясни кожен спосіб розв’язання. | Скласти та розв’язати задачу № 824 (ІІ клас). Розглянь таблицю. Повтори, які величини відомі у задачі, яка величина є сталою. Згадай, як знайти невідому кількість, знаючи ціну та вартість. Знайди. Згадай, як знайти невідому ціну, знаючи кількість і вартість. Запиши розв’язання задачі. | Розв’язати задачу № 423 (ІІІ клас). Прочитай задачу. Повтори її, користуючись коротким записом. |
| Садили 2 дні по 246 дерев і 3 дні по 336 дерев. | Залишилося у 5 разів менше, ніж посадили - ? | ||
| Склади план розв’язання та запиши розв’язання задачі. |
Для того, щоб здійснювати особистісно-зорієнтований підхід до організації навчального процесу та полегшити окремим дітям сприймання певних видів задач, слід використовувати опорні схеми, представлені у таблиці № 11.16. За допомогою цих схем можна виконувати різноманітні завдання: 1) складіть задачу за схемою (у віконечках виставляються відповідні числа); 2) назвіть дію, з допомогою якої розв’язується кожна із задач; 3) поясніть, чому задача за вказаною схемою розв’язується саме такою дією; 4) які з задач розв'язуються дією додавання, а які – віднімання? 5) запишіть, як знайти х у кожній з таких схем; 6) за яким правилом знаходимо значення х у кожній задачі?
Таблиця № 11.16.
 ÿ ÿ ÿ ÿ
Х |   І - ÿ на ÿ більше, ніж І - ÿ на ÿ більше, ніж
 ІІ – х ІІ – х
|   І - ÿ І - ÿ
 ІІ - х на ÿ більше, ніж ІІ - х на ÿ більше, ніж
| |||
    І - ÿ на ÿ на менше, ніж І - ÿ на ÿ на менше, ніж
 ІІ - х ІІ - х
|   І - ÿ І - ÿ
 ІІ – х на ÿ менше, ніж ІІ – х на ÿ менше, ніж
|   І - ÿ на х ÿ, ніж
?
ІІ - ÿ І - ÿ на х ÿ, ніж
?
ІІ - ÿ
|
Для тих дітей, які не можуть зразу розв’язати складену задачу, слід пропонувати до основної задачі допоміжну, яка допоможе при відшуканні шляху розв’язання складеної. Так, наприклад, для основної задачі “Якщо від дому до вокзалу їхати на автобусі, а назад йти пішки, то на весь шлях піде 50 хв. Якщо ж туди і назад їхати на автобусі, то необхідно витратити всього 20 хв. Скільки хвилин необхідно на весь шлях, якщо від дому до вокзалу і назад йти пішки?” допоміжною буде така: “1 кг цукерок і 1 кг печива коштують разом 4 грн. Відомо, що 2 кг цукерок коштують 6 грн. Скільки коштує 1 кг печива?”. У цій задачі формулювання простіше, ніж у основній, а хід її розв'язування підказує початок розв’язання основної задачі.
Для основної задачі “На ремонт дороги довжиною 80 км витрачено на 1 800 грн менше, ніж на ремонт дороги довжиною 95 км. Які витрати на ремонт кожної з доріг?” допоміжною буде задача “5 мішків картоплі важчі, ніж 2 мішки на 240 кг. Скільки кілограмів картоплі в одному мішку?”. Після розв’язання допоміжної задачі думка учнів спрямовуватиметься на відшукання вартості ремонту 1 км дороги. Якщо основною задачею буде “У бідоні, який заповнений молоком, 39 кг. У бідоні, який заповнений молоком наполовину, 22 кг. Яка маса порожнього бідону?”, то допоміжною задачею можна взяти таку “Сума двох чисел дорівнює 15. Якщо з цієї суми відняти половину першого числа, то одержимо 12. Знайти перше число”. Особливість допоміжної задачі полягає в тому, що вона позбавлена інформації, яка здатна ускладнити аналіз основної задачі. Крім того, складене для її розв’язання рівняння нагадує рівняння до основної задачі.
Особливий інтерес у методичному плані являють задачі, в яких навіть неправильне розв’язання приводить до правильної числової відповіді. Прикладом такої задачі може бути така: “Слід пофарбувати 150 рам. Один маляр може це зробити за 15 днів, а інший за 10 днів. За скільки днів виконають цю роботу обидва маляра, якщо будуть працювати разом?” (неправильне розв’язання може бути таким: 1) 10+15=25 (дн.) 2) 150:25=6 (дн.)). Сильним учням слід запропонувати знайти помилку у розв’язанні такої задачі та розв’язати її правильно. Для школярів, які відчувають певні труднощі при розв’язуванні задач за допомогою складання виразу, корисно використовувати допомогу у вигляді початку пояснення або пам’ятки. Наприклад, для задачі “Годинниковий завод випускає за хвилину 50 годинників марки “Слава”, а марки “Політ” на 35 штук менше. Скільки годинників обох марок випускає завод за одну хвилину?” Початок пояснення може мати вигляд, який представлений у таблиці № 11.17. Відповідно пам’ятка може мати вигляд, який представлений у таблиці № 11.18.
Таблиця № 11.17.
| У задачі запитується, скільки всього годинників обох марок випускає завод. Щоб дати відповідь на запитання задачі, потрібно до кількості годинників марки “Слава” додати кількість годинників марки “Політ”. Пишемо: 50 + “, бо слід знайти суму двох доданків. Другий доданок “ (або кількість годинників марки “Політ”) невідомий, ставимо дужки і пишемо (50 – 35), бо в умові сказано, що на 35 менше. Одержуємо: до 50+(Ä-Æ). |
Таблиця № 11.18.
| У задачі запитується ... Щоб дати відповідь на запитання ... Пишемо ... і пояснюємо ... Одержуємо ... |
Психолого-педагогічні та методичні дослідження дають підстави для висновку про те, що з метою особистісної орієнтації навчального процесу для школярів, які мають проблеми з висловленням своїх думок, слід пропонувати розв'язування задач за запитаннями (приклад такого розв'язування представлено у таблиці № 11.19.) чи планом, тривале використання алгоритмічних приписів, різноманітне читання виразів.
Таблиця № 11.19.
| Задача: “ Годинниковий завод випускає за хвилину 50 годинників марки “Слава”, а марки “Політ” на 35 штук менше. Скільки годинників обох марок випускає завод за одну хвилину?” |
| Розв’язання |
| 1) Скільки годинників марки “Політ” виготовляє годинниковий завод за одну хвилину? 50-35=15 (год.) 2) Скільки годинників обох марок випускає завод за одну хвилину? 50+15=65 (год.) Відповідь: 65 годинників обох марок виготовляє завод за одну хвилину. |
Для того, щоб навчити учнів умінню відшуковувати різні способи розв'язування задачі корисно використовувати такі особистісно-орієнтовані методичні прийоми роботи: 1) проведення аналізу задачі різними способами; 2) прийом відшукання розв’язання задачі за заданим планом; 3) прийом продовження розпочатого розв’язання (він представлений у таблиці № 11.20. для задачі “ Слід пофарбувати 150 рам. Один маляр може це зробити за 15 днів, а інший за 10 днів. За скільки днів виконають цю роботу обидва малярі, якщо будуть працювати разом?”); 4) прийом наочної інтерпретації задачі (для задачі “Довжина городу прямокутної форми 72 м, а ширина у 2 рази менша. 3/4 площі зайнято овочами, а решта – картоплею. Скільки квадратних метрів городу зайнято картоплею?” він представлений у таблиці № 11.21.); 5) порівняння розв’язань задач (такі вправи слід використовувати і для тих учнів, у яких на сформовано прийоми спостереження та порівняння (див. таблицю № 11.22..).
Формуванню уміння розв'язувати складені задачі та особистісній орієнтації навчального процесу сприяє виконання завдань на знаходження різних способів розв'язування задачі. Вони дозволяють кожному учневі відповідно до його індивідуальних особливостей проявити свої здібності, бо одні учні знайдуть один спосіб розв’язання, інші – два, треті – більшу кількість способів розв’язання, якщо це можливо. Розв'язування задач різними способами досить часто ґрунтується на різноманітних властивостях арифметичних дій або на правилах, які випливають з них. Наприклад, задача “Із двох міст, відстань між якими дорівнює 846 км, вийшли одночасно назустріч один одному два поїзди. Якою буде відстань між поїздами, коли один пройде 324 км, а інший – 286 км?” допускає способи розв’язання, які представлені у таблиці № 11.23.
Таблиця № 11.20.
| Продовж розв’язання задачі |
| 1) 150:15=ð (р.) 2) 150:Ñ=Ä (р.) 3) ð+Ä=Æ (р.) 4) 150:Æ=D (дн.) Відповідь: |
Таблиця № 11.21.
| ¾ | 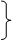
| ||
| Овочі | Картопля |

72 м
Таблиця № 11.22.
| Задача № 1 | Задача № 2 |
   Миколка зібрав 4 кг макулатури
Василько - ? на 2 кг більше, ніж Миколка зібрав 4 кг макулатури
Василько - ? на 2 кг більше, ніж
| 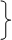   Миколка зібрав 4 кг макулатури
? кг Миколка зібрав 4 кг макулатури
? кг
 Василько – на 2 кг більше, ніж Василько – на 2 кг більше, ніж
|
| Доведіть, що задача № 2 складена! | |
| На картці подається короткий запис умови задачі й запитання щодо її аналізу, наприклад: | |
  Володя прочитав 5 книжок.
? Володя прочитав 5 книжок.
?
 Іринка - ? на 3 книжки більше, ніж Іринка - ? на 3 книжки більше, ніж
| |
| Що необхідно знати, щоб дати відповідь на запитання задачі? Що із цих даних нам невідомо? Що необхідно знати, щоб визначити кількість книжок, які прочитала Іринка? Що слід знати, щоб визначити скільки книжок разом прочитали діти? |
Таблиця № 11.23.
| І спосіб | ІІ спосіб | ІІІ спосіб |
| 846–(324+286)=236 (км) | (846-324)–286=236 (км) | (846-286)–324=236 (км) |
З метою формування навичок самоконтролю, розвитку учнів і для особистісної орієнтації навчального процесу корисно використовувати перевірку розв’язання задачі різними способами: способом складання і розв'язування оберненої задачі; способом встановлення відповідності між числами, одержаними в результаті, і даними в умові. Вказані способи представлено у таблиці № 11.24. Задача “Від двох пристаней, відстань між якими 177 км, одночасно назустріч один одному вийшли теплохід, зі швидкістю 32 км/год, та катер. Зустріч відбулася через 3 год. Яка швидкість катера?” допускає різні способи перевірки. Саме тому пропонуємо студентам виконати завдання № 27 для самостійної роботи.
Таблиця № 11.24.
| Спосіб складання і розв'язування оберненої задачі. | Спосіб встановлення відповідності між числами, одержаними в результаті та даними в умові. | ||
| Дана задача: “Із пачки взяли 18 зошитів. Після цього у пачці залишилося у 2 рази менше зошитів, ніж було. Скільки зошитів було у пачці спочатку?” | Обернена задача: “У пачці було 27 зошитів. Із неї взяли 18 зошитів. У скільки разів зошитів залишилося менше, ніж було?” | “З двох пунктів, відстань між якими 150 км виїхали одночасно назустріч один одному аеросани, зі швидкістю 60 км/год, та лижник. Зустріч відбулася через 2 год. Знайти швидкість лижника.” (Цю задачу найдоцільніше перевірити способом встановлення відповідності між числами, даними в умові та числами, які одержимо у відповіді) | Розв’язання: 1) 60·2=120 (км) 2) 150-120=30 (км) 3) 30:2=15 (км/год) |
| Перевірка: 1) 15·2=30 (км) 2) 60·2=120 (км) 3) 30+120=150 (км) |
Оскільки учні з високою та доброю успішністю виділяють математичні відношення між даними величинами та між даними та шуканими здебільшого вже під час первинного сприймання задачі, то, ознайомлюючи їх із задачею, що має знайому структуру, слід надавати їм якомога більше самостійності. Це пояснюється тим, що вони, абстрагуються від несуттєвих і наочних елементів предметної ситуації, в змозі самостійно знайти відразу шлях до розв’язання задачі, бо відповідно до сприйнятої загальної її структури вони розрізняють зміст запитання, дані та шукані величини. Як справедливо зазначає з цього приводу С.Д.Максименко, такий підхід до організації роботи із школярами є одним з основних чинників їх успішної навчальної діяльності [Максименко С.Д. Індивідуальні способи розв'язання задач //Психолог. - 200???. № ???. – С.]..
Аналіз психолого-педагогічної та методичної літератури (роботи М.В.Богдановича, Ю.М.Колягіна, С.Д.Максименка та ін.) дозволив серед учнів як із високою, так і з низькою успішністю виділити принаймні три якісно різні групи відносно розв’язання графічно оформлених задач. До першої групи слід віднести учнів, які, шукаючи шлях розв’язання задачі, враховують лише текст умови, не звертаючи уваги на графічну схему. Таке явище пояснюється принаймні двома обставинами: невмінням учнів читати графічну схему та суттєвим переважанням в їхньому індивідуальному способові мислення словесно-логічних компонентів. Звідси з необхідністю випливає напрямок особистісно-орієнтованих дій вчителя. Якщо діти не вміють читати графічну схему, то їх треба цьому вчити, а якщо у них переважають словесно-логічні компоненти мислення, то вчитель повинен потурбуватися про розвиток образного компонента мислення.
Для учнів другої групи характерне звертання лише до схеми графічного запису умови, бо графічна схема була для них самостійною задачею, що за своїми ознаками простіша. Вона була для них подібною до прикладів на обчислення суми, різниці тощо. Учні цієї групи звертаються до графічної схеми задачі тільки за спеціальною вказівкою вчителя навіть у тих випадках, коли за схемою розв’язати задачу не змогли. Для учнів третьої групи характерне звертання в одних випадках до тексту умови, а в інших – до графічної схеми. У школярів цієї групи не помічається переважання словесного чи графічного сприймання, хоч те і друге виявлялося по-різному – залежно від типу розв’язуваних задач. Отже, в учнів даної групи різко переважають наочно-дієві компоненти розумової діяльності над словесно-логічними. Завдяки тому, що вказана індивідуальна особливість у дітей з низькою успішністю веде до майже повного розриву між теоретичними знаннями і практичними вміннями, то згодом цей розрив детермінує різке зниження математичних здібностей.
У дітей третьої групи відношення показників успішності під час розв’язання задач на основі схеми й тексту як для учнів з високою успішністю, так і для учнів з низькою успішністю корелюються. Саме тому у дітей даної групи немає значного переважання наочно-образних чи словесно-логічних компонентів мислення в індивідуальних способах розумової діяльності. Разом з тим, учні з низькою успішністю і за знаннями теоретичного матеріалу, і за практичними уміннями мають нижчі показники, ніж відповідно учні з низькою успішністю із першої та другої груп. На думку С.Д.Максименка, саме в учнів з низькою успішністю третьої групи найменше розвинулися математичні здібності, тоді як учні з високою успішністю цієї самої групи набули найбільшого розвитку: вони опанували теоретичний матеріал і практичні вміння, що зумовлено органічним зв’язком між наочно-образними і словесно-логічними компонентами розумової діяльності.
На основі аналізу психолого-педагогічної і методичної літератури встановлено, що учні з переважанням словесно-логічного компоненту мислення у процесі сприймання графічної схеми стислого запису умови задачі орієнтується переважно на ключові слова, які розкривають відношення між величинами, але не звертають уваги на інші елементи схеми чи тексту задачі. В результаті експериментальних досліджень встановлено, що якщо із графічної схеми вилучити ключові слова, то учні даної групи відмовляються від розв’язання задачі, а коли вилучити графічні елементи, зберігаючи ключові слова, то вони не звертають уваги на недоліки схеми й намагаються розв’язати задачу. Наслідком цього стає те, що діти правильно чи помилково використовують один із знайомих способів розв’язання, спираючись на відповідне ключове слово: ”більше – значить треба додавати, менше – слід віднімати” [Максименко С.Д. Індивідуальні способи розв'язання задач //Психолог. - 200???. № ???. – С.].
Вивчення питання про те, чому учні з низькою успішністю та кращим розвитком наочно-образних компонентів розумової діяльності не звертаються до графічної схеми стислого запису умови при відшуканні шляху розв'язування задачі дозволяє зробити наступні висновки: 1) вони сприймають її лише як подану в зоровому плані систему наочних символів, як фігуру, яка потребує способу дій; 2) вони не спроможні розчленовувати її на окремі елементи; 3) вони не можуть встановити зв’язок між елементами та окремими даними й математичними відношеннями задачі; 4) вони асоціюють сприйняту графічну схему в своєму мисленні з баченою раніше схемою іншої задачі, не помічаючи навіть незначних графічних розбіжностей між цими схемами, які спричиняють радикальну зміну способу розв’язання; 5) вилучення із пропонованої схеми ключових слів не заважає їм обирати правильний чи помилковий спосіб розв’язання задачі. Знаючи вказані причини відносно кожного учня, вчитель початкових класів має можливості для реалізації у навчальному процесі особистісно-орієнтованого підходу до молодших школярів. На жаль, як свідчать проведені дослідження ці можливості не реалізуються в практиці роботи більшості вчителів, навіть незважаючи на те, що у методичній літературі та в досвіді роботи вчителів-новаторів можна знайти досить значну кількість методичних прийомів, які дозволять при такій організації навчання учнів розв’язувати текстові задачі усунути названі типові помилки.
Аналіз психолого-педагогічної та методичної літератури, проведені експериментальні дослідження дозволили виділити учнів з низьким темпом виконання завдань і встановити, що такий темп може бути обумовлений низьким рівнем розвитку навіть тільки одного із компонентів навчальної діяльності. С.Д.Максименко встановив, що відставання одного компонента детермінує загальну затримку розумового розвитку, бо іншим компонентам при цьому також не вистачає належного тренування. Разом з тим, для таких дітей властиві: 1) невміння узагальнювати математичний матеріал; 2) намагання при відшуканні шляху розв’язування задачі та під час її розв’язування безпосередньо використовувати один із не багатьох способів дії без свідомого аналізу нового завдання; 3) відсутність запитань про відповідність чи невідповідність, про доцільність чи недоцільність обраного способу розв’язування; 4) неточність, помилковість, наявність смислових відхилень при відтворенні математичного матеріалу; 5) відсутність нової орієнтувальної основи для сприймання математичного матеріалу; 6) інертність і бідність думки; 7) обмеженість у пошуках математичного змісту ситуації, описаної в умові задачі; 8) необхідність прикладання значних зусиль для того, щоб відмовитися від попередньо обраної схеми, гнучко змінити шлях розв’язування задачі. Вказані індивідуальні особливості вимагають від вчителя застосування особистісно-орієнтованого підходу для подолання вказаних недоліків. Відсутність такої організації навчального процесу чи необізнаність вчителя із вказаними особливостями з необхідністю призводить до закріплення вказаних недоліків і до зниження успішності навчання молодших школярів [Максименко С.Д. Індивідуальні способи розв'язання задач //Психолог. - 200???. № ???. – С.].
Проведені дослідження свідчать, що школярі з низькою успішністю шукають шлях розв'язування задачі йдучи від її конкретного або числового змісту до схематичного уявлення загальної її математичної структури. Не маючи достатнього рівня схематизації, вони не можуть осягнути числовий зв’язок ні між частинами задачі, ні між назвами величин та їх числовими значеннями, ні між умовою та запитанням. Саме знання цієї відмінності (а точніше незнання її більшістю вчителів!) у розумінні задач між учнями з високою та низькою успішністю слід, з одного боку, вважати основою для особистісно-орієнтованого формування уміння розв'язувати задачі у молодших школярів, а з іншого – значними недоліками у сформованості цього уміння у більшості школярів [Максименко С.Д. Індивідуальні способи розв'язання задач //Психолог. - 200???. № ???. – С.].
Читайте також:
- В якій камері утворюється малюнок у сирі швейцарському?
- Малюнок 11.1.
- Малюнок 11.2.
- Малюнок 11.7.
- Малюнок 16.2 - Крива сукупної пропозиції
- Малюнок 7.2.1. Етап проектування.
- Малюнок 8.1.
- Малюнок 8.3.
- Малюнок 8.4.
- Малюнок 8.5.
- Малюнок 8.7 - Види еластичності попиту
| <== попередня сторінка | | | наступна сторінка ==> |
| Малюнок 11.2. | | | ТМО навчання учнів розв'язувати типові складені задачі на знаходження четвертого пропорційного. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |
