• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Кореляція цінних паперів та її застосування.

Як правило, інвестор купує декілька видів цінних паперів. У зв'язку з цим важливою є ще одна характеристика, що торкається пари цінних паперів. Вона характеризує взаємозв'язок між нормами прибутку двох цінних паперів. Називають її кореляцією цінних паперів. Поняття кореляції подамо на при­кладі двох звичайних акцій.

Міру (ступінь) щільності взаємозв'язку між двома акціями (точніше, між нормами прибутку двох акцій) вимірюють за допомогою коефіцієнта кореляції. Якщо розглядають дві різні звичайні акції А та В, позначені відповідно номерами 1 та 2, то коефіцієнт їх кореляції визначають за формулою:

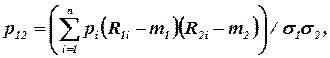
де р₁₂ – коефіцієнт кореляції першої і другої акції;

m₁ – очікувана норма прибутку першої акції;

m₂ – очікувана норма прибутку другої акції;

R_1t – можлива норма прибутку першої акції (i = 1…. n);

R_2t – можлива норма прибутку другої акції (i = 1….n);

рi – вірогідність відповідно можливих норм прибули (i = 1….n);

σ₁, σ₂ – середньоквадратичне відхилення відповідно першої та другої акції.

Коефіцієнт кореляції двох акцій кiлькiсно оцінює щільність взаємозв'язку норм прибутку цих акцій між собою.

Приведемо деякі з його основних властивостей.

1. Коефіцієнт кореляції приймає значення в межах [-1,..1]

2. Абсолютна величина коефіцієнту кореляції вказує на силу взаємозв'язку норм прибутку акцій, тому чим вищою є абсолютна величина, тим міцніше між собою пов’язані ці акції. Найміцніше пов'язані між собою ті дві різні акції, коефіцієнт кореляції яких мало відрізняється від 1 чи - 1, а слабо пов'язаними ті, у яких коефіцієнт кореляції є близьким до нуля.

3. Знак коефіцієнта кореляції вказує напрямок взаємозв’язку норм прибутку акцій. Якщо він додатній, маємо так звану додатну кореляцію. Це означає, що зростання (зниження) норми прибутку однієї акції відбувається одночасно зі зростанням (зниженням) норми прибутку другої акції. Коли ж коефіцієнт кореляції є від’ємною величиною, то маємо коефіцієнт так званої від’ємної кореляції акцій. Це означає, що зростання (зниження) норми прибутку однієї акції відбувається одночасно зі зниженням (зростанням) норми прибутку другої акції.

На практиці додатна кореляція зустрічається частіше, ніж від'ємна. Це пов'язано з так званою силою зростання ринку. Наприклад, дослідження, що були проведені на Нью-йоркській біржі, показали, що переважна частина акцій має коефіцієнт кореляції у межах 0,4...0,6.

Аналогічно тому, як це було зроблено при розрахунку сподіваної норми прибутку та ризику при обчисленні коефіцієнта кореляції акцій, можна скористатися інформацією відносно норм прибутку акцій у минулому.

Формула для обчислення коефіцієнта кореляції двох акцій приймає при цьому такий вид:

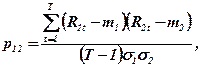
де Т - кількість попередніх періодів, для яких маємо інформацію;

R_1t — норма прибутку першого цінного паперу в t-му періоді;

R_2t— норма прибутку другого цінного паперу в t-му періоді;

m₁—сподівана норма прибутку першого цінного паперу;

m₂—сподівана норма прибутку другого цінного паперу;

"σ₁", "σ₂" —ризик (середньоквадратичне відхилення) відповідно першого та другого цінних паперів.

Проілюструємо характерні випадки щодо різних значень коефіцієнта кореляції двох акцій (рис. 4.1).

Рис. 9.1. Коефіцієнт кореляції двох акцій:

близький до 1 (а), до - 1 (б) та до 0 (в)

На рис. 4.1 на осі абсцис відкладені різні можливі значення норм прибутку деякої гіпотетичної акції 1, а на осі ординат— різні можливі значення норми прибутку гіпотетичної акції 2, що мали місце у минулі періоди.

З рис. 4.1(а) видно, що множина точок, координатами яких є можливі значення норми прибутку акції 1 і 2 за ті самі періоди, дуже щільно сконцентрована навколо деякої зростаючої прямої лінії.

Високим (низьким) нормам прибутку однієї акції відповідають за ті ж періоди високі (низькі) норми прибутку другої акції. З рис. 4.1(б) видно, що відповідна множина точок, кожна з яких характеризує значення норми прибутку акції 1 та 2 за один період, дуже щільно сконцентрована навколо деякої спадаючої прямої. Високим (низьким) нормам прибутку одній акції відповідають за той самий період низькі (високі) норми прибутку другої акції.

З рис. 4.1(в) видно, що відповідна множина точок не сконцентрована навколо будь-якої лінії. Можна говорити про відсутність якоїсь кореляційної залежності між нормами прибутку цих двох акцій за різні періоди. Коефіцієнт кореляції цих двох акцій є близьким до нуля.

Читайте також:

1. Автокореляція
2. Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
3. Акти правозастосування.
4. Аналіз в управлінні портфелем цінних паперів.
5. Антисептики ароматичного ряду (фенол чистий, іхтіол, дьоготь, мазь Вількінсона, лінімент за Вишневським). Особливості протимікробної дії та застосування.
6. Аудит цінних паперів.
7. Бактеріофаг, його природа і практичне застосування. Вплив бактеріофага на мінливість мікроорганізмів.
8. Банки як учасники ринку цінних паперів
9. Будова СВА. Стандарти практичного застосування.
10. Види освіти, особливості повноцінних знань
11. Види освіти, особливості повноцінних знань
12. Види цінних паперів та їх основні характеристики.

Переглядів: 1679