• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Портфель з двох різних акцій.

Узгодження максимізації норми прибутку і мінімізації ризику не є простим, бо на досить ефективному ринку цінні папери з високою нормою прибутку характеризуються відповідно високим ступенем ризику. Розсудливий інвестор шукає такі можливості розміщення капіталу, за яких зі збільшенням норми прибутку одночасно, зменшувався б ступінь ризику. Такі можливості дає йому формування портфеля цінних паперів. Сукупність придбаних цінних паперів складає їх портфель.

Особливим випадком є однорідний портфель, тобто такий, котрий містить лише один вид цінних паперів. Подібно до того як у випадку одного виду цінних паперів, так і у випадку портфеля двох акцій основними характеристиками можна обрати норму прибутку і ризик.

Припустимо, що портфель утворюють дві різні акції А та В, відповідно з номерами 1 та 2. Позначимо сподівані норми прибутку цих акцій через m1 та m2, варіації через V1 та V2, а середньоквадратичні відхилення через "σ1" та "σ2".

Припустимо, що інвестор посідає портфель, до якого входять 100 акцій певної дніпропетровської фірми (1) та 200 акцій певного київського підприємства (2). Ціна однієї акції з номером 1 становить 500 грн., а однієї акції 2 – 200 грн.

Знайдемо частку вартості кожного виду акцій в портфелі:

х₁ = (100 • 500)/(100 • 500 + 200 • 200) = 0,56;

х₂ = (200 • 200)/(100 • 500 + 200 • 200) = 0,44.

Очевидно, що частка кожної акції в портфелі є величиною в інтервалі від 0 до 1:

х₁+х₂=1; (0 ≤ х ≤ 1)

Частки можна трактувати як частини від одиниці капіталу (грошей), що вкладені у відповідний вид цінних паперів. Знаючи сподівані величини норми кожної з цих акцій та їх частки в портфелі, легко визначити сподівану норму прибутку портфеля з двох акцій за формулою

m_p = x₁m₁ +x₂m₂

де m_p — норма прибутку портфеля з двох різних акцій.

Як бачимо , норма прибутку портфеля двох акцій є зваженою середньою нормою прибутку кожного виду акцій, при цьому ваговими коефіцієнтами виступають частки цих акцій (у грошовому обсязі) в портфелі.

Приклад. Інвестор посідає портфель, що складається з двох акцій А та В з нормами прибутку відповідно 20% та 25%, причому частка акції А становить 40% портфеля. Підрахуємо норму прибутку портфеля.

m_p= 0,4 × 20% + 0,6 × 25% = 23%.

Слід зазначити, що норма прибутку портфеля з двох акцій завжди знаходиться в інтервалі, границями якого є норми прибутку акцій, що входять до складу портфеля.

Визначимо ризик портфеля двох акцій, умовно позначених номерами 1 і 2. Виявляється, що варіація портфеля двох акцій може бути обчислена за формулою:

V_p = x₁²σ₁² + x₂²σ₂² + 2х₁х₂σ₁σ₂р₁₂.

де V_p— варіація портфеля двох акцій; р₁₂ — коефіцієнт кореляції двох акцій.

Середньоквадратичне відхилення портфеля двох акцій визначається за формулою:

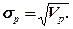
Варіація (а отже ризик портфеля) двох акцій залежить не лише від ризику кожного виду акцій, що залучені до його складу, але також від кореляції цих акцій, тобто від ступеня взаємозалежності (взаємозв'язку) між їхніми нормами прибутку.

Далі більш детально проаналізуємо вплив кореляції на ризик портфеля.

Як відшукати структуру капіталу, що забезпечить його мінімальний ризик? Виходячи з вищенаведених формул:

х₂ =1- х₁

V_p = x₁²σ₁² + (1- x₁)²σ₂² + 2x₁ (1 – x₁) σ₁ σ₂ p₁₂

Мінімум V_pможна знайти, якщо прирівняти до нуля першу похідну V_pякфункції від х₁.

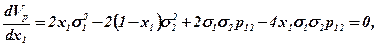
звідси одержимо, що це виконується при таких х*₁ та х*₂:

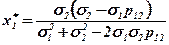
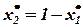
Формування оптимального портфелю цінних паперів, що складається з двох акцій можна проілюструвати графічно вдвовимірному просторі, де на осі абсцис відкладатимемо значення ризику (середньоквадратичні відхилення), а на осі ординат значення сподіваної норми прибутку (рис. 4.2).

Розглянемо випадок, коли р₁₂ = 1. Це один з екстремальних випадків, який означає абсолютну додатну кореляцію (функціональну залежність) між нормами прибутку двох акцій.

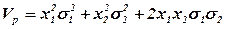
чи

V_р = (х₁σ₁ + х₂σ₂)².

Отже, ризик портфеля, виражений як середньоквадратичне відхилення в цьому випадку, дорівнює

σ_р = х₁σ₁ + х₂σ₂

Як бачимо у випадку абсолютної додатної кореляції між нормами прибутків певних акцій, ризик портфеля є середньо­зваженою величиною ризику окремих видів акцій, що входять до його складу. А ваговими коефіцієнтами е частки цих акцій в портфелі.

Підставляючи різні значення х₁ та х₂, причому х₁ + х₂ = 1, тобто змінюючи структуру портфеля, визначатимемо значення сподіваної норми прибутку та ризику множини усіх допустимих портфелів двох акцій.

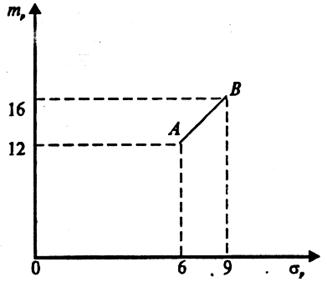
Рис. 4.2. Множина портфелів двох абсолютно додатньо

корельованих видів акцій

Слід зазначити, що точка А відповідає портфелеві, що скла­дається лише з акцій А, а точка В – портфелеві, котрий скла­дається лише з акцій В. Середина відрізку АВ відповідає порт­фелеві, де обидві акції мають частку х1 = х2 = 0,5.

Як бачимо, випадок абсолютної додатної кореляції акцій не дозволяє досягнути якогось суттєвого ефекту. Зменшуючи ризик, ми одержуємо прямо пропорційне зменшення сподіваної норми прибутку і навпаки. Цей випадок не цікавий для інвес­тора, бо тут дуже обмежене поле щодо маневру.

Розглянемо випадок, коли р₁₂= -1. Цей екстремальний випадок означає абсолютну від'ємну кореляційну залежність (функціо­нальну залежність) між нормами прибутку двох акцій.

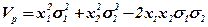
чи

V_p = (x₁σ₁ – x₂σ₂)².

Ризик портфеля, виражений як середньоквадратичне відхи­лення в цьому випадку дорівнюватиме

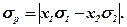
Аналіз рівняння показує, що ризик портфеля в цьому особливому випадку можна суттєво зменшити. Якщо "σ_р" прирівняти до нуля, а цього можна досягнути за умови, коли

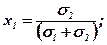
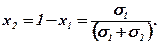
Тобто у випадку абсолютної від'ємної кореляції є можливість обрати таку структуру портфеля, котрий цілком позбавлений ризику.

Аналогічно попередньому проілюструємо цей приклад графічно (рис. 4.3).

Рис. 4.3. Множина портфелів з двох абсолютно від’ємно

корельованих акцій

Для цього випадку множина усіх допустимих портфелів складається з точок ламаної АСВ. Точки А та В відповідають портфелям, що складаються лише з одного виду акцій (А та В вiдповiдно).

Слід зауважити, що виходячи з точки А і збільшуючи в портфелі частку акції В, отримуємо зростання норми прибутку і одночасне зменшення ступеня ризику. В точці С маємо портфель з нульовим ступенем ризику.

Коли ж частка акції В і далі зростатиме, то маємо подальше зростання норми прибутку портфеля. Однак, ризик тепер теж зростає до величини σ2.

З рисунку маємо, що розсудливий менеджер (інвестор) напевне не обере жодного портфеля розташованого на відрізку АС. Для кожного такого портфеля знайдеться кращий (з іншою структурою), якому відповідають точки відрізка CD. Кращий тому, що за тим самим ступенем ризику дає більшу норму прибутку. Відрізок СВ називають множиною ефективних портфелів.

Розглянемо випадок, коли р₁₂=0. Цей випадок означає відсутність взаємозв'язку (взаємозалежності) між акціями, тобто формування норми прибутку однієї акції ніяк не пов'язане з формуванням норми прибутку другої акції.

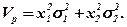
Ризик портфеля, виражений як середньоквадратичне відхилення, визначається за формулою

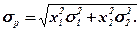
З формули випливає, що є можливість часткової редукції ризику портфеля двох акцій. Підставляючи в формулу значення х₂ = (1 - х₁), обчислимо першу похідну функції σ_р.

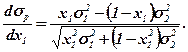
Величина σ_р досягає свого мінімуму за умови, що:

dσ_p / dx₁ =0

а це можливо, коли

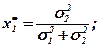
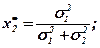
Мінімальне значення ризику дорівнює

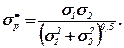
Приклад. Маємо дві різні звичайні акції А та В, позначені номерами 1 та 2. Нехай сподівані норми прибутку від цих акцій дорівнюють відповідно m₁ =40%, m₂ = 60%, а ризик σ₁ = 5%, σ₂ = 8%, коефіцієнт кореляції між нормами прибутку за цими акціями р₁₂=0. Обчислити та проаналізувати сподівану норму прибутку та ризику портфелів, які можливо сформувати з цих акцій.

m_р = x₁ × 40% + x₂ × 60%, σ_р = (х₁² • 25 + х₁² • 64)^0,5.

Як і у попередньому випадку, проілюструємо цей приклад графічно (рис. 4.4). Цього разу усі допустимі портфелі розташовані на кривій АВ.

Точки А та В знову ж відповідають портфелям, в які входять лише акції виду А та В відповідно.

Відзначимо що, виходячи з точки А і збільшуючи частку акцій В у портфелі, отримуємо зростання норми прибутку i зниження ступеня ризику.

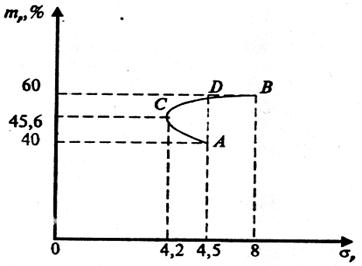
Рис. 4.4. Множини портфелів із двох некорельованих видів акцій

Доходячи до точки С, отримуємо портфель з мінімально можливим ступенем ризику. Також легко відшукати частки акцій А та В в цьому портфелі:

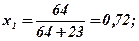х₂ = 0,28.

Ризик цього портфеля до­рівнює 4,24%, а норма прибутку буде:

m_c = m_р = 0,72 × 40% + 0,28 × 60 % = 28,8 + 16,8 = 45,6 %.

Збільшуючи надалі частку акцій В в портфелі (х₂ > 0,28) отримуємо подальше зростання норми прибутку портфеля. При цьому ризик теж зростає відносно своєї мінімальної величини. З рис. 4видно, що розсудливий інвестор напевне не обере жодного з портфелів, котрі знаходяться на відрізку АС кривої. Для кожного такого портфеля знайдеться кращий, що зна­ходиться на відрізку кривої CD. Він кращий, бо при такому ж ступені ризику дає більше значення норми прибутку. Відрізок СВ кривої є множиною ефективних портфелів.

Наведені вище приклади показують, що вміле формування портфеля з двох видів акцій може призвести до значного змен­шення ризику. Ясно, що залучення до портфеля, котрий скла­дався лише з одного виду акцій, другого виду акцій, призводить майже завжди до зниження ризику, часом навіть при одно­часному зростанні норми прибутку портфеля. Такі дії інвестора (менеджера) називаються диверсифікацією.

Розрізняють «наївну» диверсифікацію та «розсудливу». «Наїв­на» диверсифікація спирається на максимальну різноманітність залучених до портфеля різних видів цінних паперів без точного використання ступеня кореляції (зв'язку) між ними. Така дивер­сифікація, як правило, рідко призводить до значної редукції ри­зику, як це показано у випадку зі звичайними акціями з великим від'ємним (близьким до мінус одиниці) коефіцієнтом кореляції. «Розсудлива» диверсифікація повинна враховувати кореляцію між цінними паперами. Не мають рації ті, хто вважає, що до фор­мування портфеля не конче потрібно використовувати економіко-математичні методи та моделі.

Читайте також:

1. Адаптаційні зміни суглобово-зв'язкового апарату спортсменів різних спеціалізацій.
2. Акціонерні товариства випускають облігації на суму не більше 25 % від розміру статутного капіталу і лише після повної оплати всіх випущених акцій.
3. Але різних за значенням
4. Але різних за значенням.
5. Арифметичні операції в різних системах числення
6. Банківська система в ринковій економіці є звичайно дворівневою і включає центральний банк (емісійний) і комерційні (депозитні) банки різних видів.
7. В однакових об'ємах різних газів за однакових умов (температура і тиск) міститься однакова кількість молекул.
8. В умовах різних облікових систем
9. Вибори, їх класифікація та особливості при різних політичних режимах.
10. Вибори, їх класифікація та особливості при різних політичних режимах.
11. Види планів щодо різних критеріїв
12. ВИДИ СПОСТЕРЕЖЕННЯ В РІЗНИХ ТИПАХ ДОСЛІДЖЕННЯ

Переглядів: 3084