• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Портфель з багатьох акцій.

Перейдемо тепер до загального випадку, коли до складу портфеля залучено багато різних акцій.

Введемо такі позначення: n – кількість різних акцій, які входять до портфелю, що пронумеровані від 1 до n; m_i – сподівана норма прибутку i-й акції , σ_i – ризик (розраховується як середньозважене відхилення) i-й акції 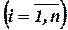, р_ij – коефіцієнт кореляції i-й и j-й акцій 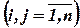, (i ≠ j), х_i - часка i-й акції, що включається до портфелю .

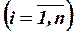Очевидно, що

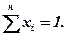
Аналогічно, як і у випадку двох різних акцій, так і в за­гальному випадку, потрібно вміти обчислювати сподівану норму прибутку i ризик портфеля.

Це здійснюють за допомогою таких формул:

;

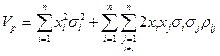σ_р = (V_р)^0,5,

де т_р— сподівана норма прибутку портфеля акцій,

V_р — варіація (дисперсія) портфеля акцій,

σ_р - середньоквадратичне відхилення (ризик) портфеля акцій.

Варіацію, тобто ризик порт­феля, можна трактувати як суму двох складових. Перша складова віддзеркалює індивідуальний ризик кожної з акцій. Оскільки це середньозважена варіацій окремих акцій (ваговими коефіцієн­тами виступають квадрати часток акцій в портфелі); друга скла­дова характеризується взаємозв'язками між парами акцій Тобто показує вплив коефіцієнтів кореляції пар акцій на ризик портфеля: від'ємні величини коефіцієнтів кореляції призводять до зменшення варіації портфеля.

Приклад. Три акції А, В, С, пронумеровані 1, 2, 3, мають норми прибутку відповідно m₁ = 5%, m₂ = 10%, m₃ = 15% середньоквадратичні відхилення і коефіцієнти кореляції приймемо вiдповiдно σ₁ = 3%, σ₂ = 7 %, σ₃ = 10%, р₁₂ = 0,6, р₁₃ = - 0,2, р₂₃ = -0,4. Визначити допустиму множину портфелів.

Позначені літерами А, В, С вершини відповідають портфелям, що сформовані лише з однієї акції А, В, С відповідно. Частка інших двох акцій дорівнює нулеві. Необхідно зазначити, що кожен розсудливий інвестор обере будь-який з портфелів, що відповідає множині точок, котрі лежать на відрізку МС, зображеної на рис. 4.5 фігури. Дійсно, для будь-якоїіншої точки, що міститься в межах даної фігури (таких, що не лежать на кривій МС)знайдеться відповідна точка на кривій МС, для якої при тому ж значенні величини ризику, норма прибутку буде більшою.

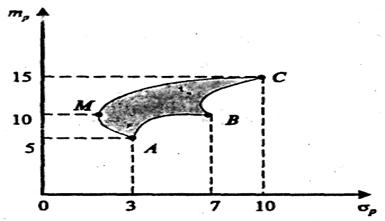
Рис. 4.5. Допустима множина портфелів з трьох акцій

Заштрихована область, точки котрої характеризують ступінь ризику та норму прибутку портфеля за усіх можливих часток окремих акцій в портфелі, називається допустимою множиною портфелів.

Відрізок кривої МС належить до допустимої множини. Але для будь-якої точки цього відрізку не можна вказати ін­шої точки допустимої множини, для якої портфель був би кращим.

Множина точок кривої МС називається ефективною мно­жиною портфелів.

Тобто ефективним портфелем з допустимої множини буде такий, для котрого не існує іншого:

· з тим самим значенням величини норми прибутку і меншим ступенем ризику;

· з тим самим значенням величини ризику і більшим значенням норми прибутку.

Нехай ми маємо "n" різних цінних паперів, кожна пара яких пов'язана між собою певною кореляційною залежністю.

Допустима множина портфелів, сформованих з цих цінних паперів, зображена на рис. 4.6, де відрізок кривої MN харак­теризує ефективну множину портфелів.

Рис. 4.6. Вибір портфеля менеджерами с ризиковими функціями корисності

Зазначимо, що опуклість кривої MN, котра характеризує ефективну множину, випливає з тих міркувань, що лінійна комбінація двох портфелів також є портфелем.

Для двох менеджерів (управлінських команд, інвесторів) по­будовані відповідні функції корисності, криві ліній байдужості яких зображені на рис. 6 (І —для першого менеджера, II — для другого менеджера).

Вибір найкращого портфеля з ефективної множини, що відповідають множині точок кривої MN, буде залежати від функ­цій корисності (схильності або несхильності до ризику).

Менеджер І обере портфель, позначений точкою N₁, яка від­повідає найбільшому значенню його корисності на ефективній множині портфелів. Менеджер II, що більш схильний до ризику, обере портфель з ефективної множини, позначений точкою N₂.

Читайте також:

1. Акціонерні товариства випускають облігації на суму не більше 25 % від розміру статутного капіталу і лише після повної оплати всіх випущених акцій.
2. Включення в портфель безризикових цінних паперів
3. Градієнт функції багатьох змінних. Похідна функції по напрямку
4. Економічні задачі, що приводять до поняття функцій багатьох змінних
5. Екстремум функції багатьох змінних
6. Екстремум функції багатьох змінних. Необхідна та достатня умови екстремуму. Критерій Рауса-Гурвіца
7. ЕНЕРГЕТИКА І КІНЕТИКА РЕАКЦІЙ.
8. Замикання тимчасових зв’язків. Нейронні кореляти формування і прояву умовно-рефлекторних реакцій.
9. Затвердження уповноваженим органом емітента результатів закритого (приватного) розміщення акцій та звіту про результати закритого (приватного) розміщення акцій.
10. Збереження документів у Портфель
11. Збереження зовнішніх файлів у Портфель
12. ИНВЕСТИЦИОННЫЙ ПОРТФЕЛЬ

Переглядів: 621