• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Загальні засади теорії портфеля цінних паперів та оптимізація його структури.

Подамо постановку та класичний розв'язок задачі.

Нехай R_it – норма прибутку i-ого цінного паперу, що наведена у відсотках за період t, 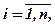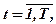де n – кількість видів цінних паперів; Т – об’єм вибірки (кількість досліджень).

Норма прибутку портфеля в періоді t дорівнює:

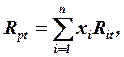
де х_i— постійний коефіцієнт, частка інвестицій в i-й цінний папір, що є залученим до портфеля.

Сума всіх часток становить

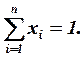
Сподіване значення (математичне сподівання) норми прибутку портфеля також є зваженою середньої очікуваної норми прибутку від окремих цінних паперів:

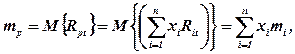
де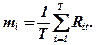

Ступінь ризику портфеля оцінюється середньоквадратичним відхиленням σр, яке обчислюється на базі варіації (дисперсії) його норми прибутку:

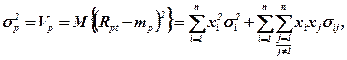
де σ_i² – дисперсія (варіація) норми прибутку i-й цінного паперу

;

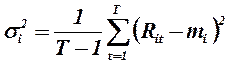деσ_ij– коваріація між нормами прибутку i-й и j-й цінних паперів:

чи

σ_ij = p_ij σ_i σ_j

Нехай норма прибутку цінних паперів з фіксованим відсотком складає R_F. Для цих паперів сподівана норма прибутку m_F теж дорівнює R_F,а ризик дорівнює нулеві, тобто m_F = R_F, σ_F = 0. Інвестуючи капітал у цінні папери, обтяжені ринковими коливаннями (ризиком), прагнуть отримати найкраще співвідношення між додатковим прибутком та зростаючим ступенем ризику.

Відкладемо на рис. 4.7 у просторі m_p — σ_рточку, що характеризує цінний папір з фіксованим прибутком R_F на осі ординат.

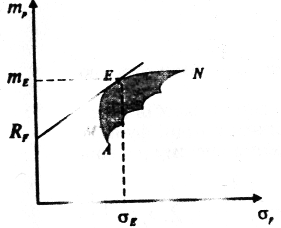
Рис. 4.7. Геометрична iнтерпретацiя оптимального портфеля

Зрозуміло, що найкраще співвідношення між приростом норми прибутку і зростанням ризику забезпечує портфель цінних паперів, що позначений точкою Е, через котру проходить дотична до лінії ефективних портфелів, яка починається в точці R_F.

Отже, оптимальною структурою портфеля буде та, що від­повідає точці Е. її можна знайти за допомогою максимізації наступної функції:

φ = (m_p – R_F) / σ_p

за умови, що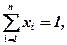

де х_i—частка капіталу, що інвестована в i-й цінний папір.

Введемо обмеження до цільової функції. Для цього запишемо R_F як

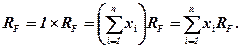
Зробив підстановку, отримуємо:

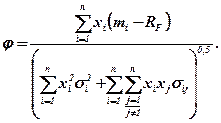
Необхідно визначити коефіцієнти x_i, що максимізують цю функцію.

Цього можна досягти за допомогою звичайних засобів математичного аналізу, прирівнявши перші часткові похідні функції ф, за шуканими параметрами до нуля. Одержимо систему рівнянь

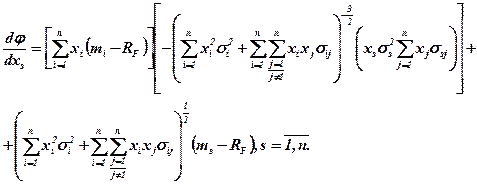
Помножив ліву та праву частину виразу на:

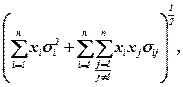
отримуємо

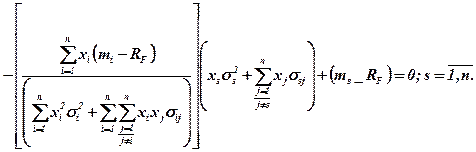
Не важко помітити, що співвідношення у квадратних дужках є константою, бо всі його складові є постійними. Позначимо його через (λ) і перепишемо у виді

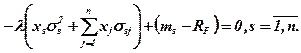
Ця система складається з «n» неоднорідних рівнянь (n+1) з невідомими: λ, x_s, .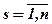

Введемо нові позначення:

y_s = λx_s;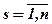

Підставив їх у початковий вираз, отримуємо систему «n» лінійних неоднорідних рівнянь відносно невідомих у_s. Розв’язавши її, та обозначивши у_s, 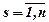, та знаючи їх, розрахуємо х_s, використовуючи:

;

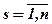
Величини x_s визначають оптимальну структуру портфеля при заданому наборі цінних паперів у формі прибутку R_F щодо паперу з фіксованим відсотком.

Але може так статися, що в результаті розв'язку системи частина коефіцієнтів х_i буде мати від'ємні значення.

Що ж робити в цьому випадку?

Якщо на коефіцієнти х_i накласти умови невід'ємності, тобто

x_i ≥ 0; i =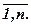

то задачу знаходження максимуму можна розв'язати за одним із методів квадратичного про­грамування. Це пов'язано з тим, що цільова функція, котру необхідно максимізувати – нелінійна, в ній містяться члени з х_i² i x_i x_j.

Рішення знаходити просто за наявності відповідного про­грамно-технічного комплексу. Якщо умови невід’ємності не накладаються, то від'ємне значення якогось з x_jозначає, що відповідні цінні папери необхідно продати на термін без покриття (to sell short), тобто при їх відсутності у продавця на час продажу. Іншими словами, йдеться про гру на пониження. Необхідно зазначити, що за кордоном більшість інституційних інвесторів не торгують цінними паперами на термін без покриття. А багатьом інституціям ця операція просто заборонена законом. Та все ж вона широко використовується, зокрема, на Нью-Йоркській та деяких інших фондових біржах і по суті є однією з форм позички.

У загальному вигляді задача щодо оптимального інвестування в цінні папери допускає як позичку, так і надання кредитів. Позичка збільшує ресурси для інвестування, а на­дання кредиту рівнозначно (в певному сенсі) інвестуванню під фіксований відсоток. Для спрощення задачі вважають, що одер­жання та надання кредиту здійснюються за тим же фіксованим відсотком R_F.

Припустимо, що інвестор вирішив вкласти частину своїх засобів у певний портфель Е і, окрім цього, надати кредит чи взяти в борг під фіксований відсоток R_F. Проаналізуємо ці ситуації.

Нехай х – частка від позичкового капіталу, котру інвестор розмістив у вигляді портфеля Е. Величина х може бути більшою ніж одиниця, оскільки можна допустити, що інвестор може скористуватися позичкою та інвестувати більше, ніж величина його власного початкового капіталу. Якщо х — частка, вкладена у портфель Е, то (1 - х) повинно дорівнювати частці засобів, розміщених під фіксований відсоток.

Сподівана норма прибутку від комбінації з позичково-кре­дитною операцією може бути визначена так:

m_p = (1 – x) R_F + xm_E

Ризик такої комбінації характеризується величиною:

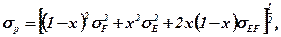
де σ_F = 0, відповідно, σ_EF = 0, тобто:

σ_р = хσ_Е

Розв’язуючи це рівняння відносно «х», отримаємо:

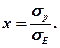
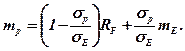
Після переробки отримуємо:

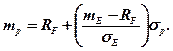
Останнє рівняння є рівнянням прямої у двомірному просторі (σ – т). Ця пряма називається лінією ринку капіталів i харак­теризує портфелі, що складаються як із цінних безризикових паперів, так і з цінних паперів, обтяжених ризиком.

Слід зауважити, що Коли х=1, тобто, коли відсутня позичково-кредитна операція, маємо, що m_p= m_E, σ_p = σ_Е.

На рис. 4.8 точка Е лежить на лінії MN (множина ефективних портфелів). Ця точка також належить до прямої R_FE, що є дотичною до множини ефективних портфелів (кривої MN):

Точку Е з координатами (σ_Е, m_E) називають ринковим портфелем.

Всі комбінації ринкового портфеля Е із позичково-кредит­ними операціями з фіксованим відсотком лежать вздовж прямої у просторі ризик — норма прибутку. Пряма перетинає вісь ординат на рівні R_F під кутом (α):

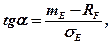
проходячи через точку Е (σ_Е, m_Е), котра репрезентує ринковий портфель (рис. 4.8).

Рис. 4.8. Комбінація оптимального (ринкового портфеля Е) з кредитно-позичковими операціями: 1 — позика, 2 — кредит

На рис. 4.8 пряма R_FN являє собою множину оптимальних розв’язань, що характеризуються пропорційним (сталим) співвідношенням приросту норми прибутку до зростання ступеня ризику.

Вибір залишається за менеджером (інвестором) залежно від його схильності до ризику.

Відрізок R_FE відображає рішення інвестувати певну частку власних засобів в портфель Е, а іншу частку віддати у вигляді позики під фіксований відсоток R_F. Вздовж відрізка ЕК розташовані рішення щодо позички додаткових засобів, а весь сумарний капітал інвестується в портфель Е. Таким чином, у будь-якому випадку пошук точки Е на множині ефективних портфелів є розв'язком проблеми щодо оптимізації структури портфеля.

Читайте також:

1. I. Загальні збори АТ
2. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
3. I. Загальні положення
4. II. ЗАГАЛЬНІ ПОЛОЖЕННЯ.
5. XXXIII. ЗАГАЛЬНІ ПРОФЕСІЇ (У ВСІХ ГАЛУЗЯХ ГОСПОДАРСТВА)
6. А .Маршалл - основоположник неокласичної теорії.
7. А) загальні критерії
8. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
9. Альтернативні теорії вартості
10. Альтернативні теорії вартості
11. Альтернативні теорії вартості
12. Альтернативні теорії капіталу

Переглядів: 844