• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Спрощена класична модель формування портфеля цінних паперів.

Найпростішою і широко використовуваною на практиці математичною моделлю для наближених розрахунків є запропонована Вільямом Шарпом однофакторна модель.

Ця модель ґрунтується на багаторічних спостереженнях і виявленні того факту, що норми прибутків більшості акцій, в ос­новному, залежать від одного чинника, котрий називають чин­ником ринку (біржі). На більшості бірж спостерігається, що зі зростанням ринкових індексів зростають пропорційно і ціни біль­шості акцій і навпаки. Ці спостереження дозволили висунути гіпо­тезу, згідно з якою норми прибутку акцій щільно корельовані віднос­но загальнобіржового індексу доходів (середньому по біржі в цілому). Цей індекс можна трактувати як гіпотетичний цінний папір (акцію), ціна котрого весь час коливається, і для якого, зокрема, можна визначити сподівану норму прибутку та варіацію. Цей гіпотетичний цінний папір можна прийняти за портфель ринку. Кореляційну залежність норми прибутку звичайних акцій від норми прибутку, котру вказує ринковий індекс, у середньому можна подати за допомогою рівняння регресії:

m_i = a_i + β_im_M +e_i,

де m_i — сподівана норма прибутку i-й акції;

m_M — сподівана норма при­бутку ринку (ринкового портфеля, до якого залучена і дана акція);

a_i, β_i— коефіцієнти рівняння регресії;

е_i — випадкова складова рівняння регресії.

Ця формула називається характеристичною лінією цінного паперу, в даному випадку це — характеристична лінія i-й акції.

У цьому рівнянні норма прибутку певної акції «пояснюється» нормою прибутку ринку. Звичайно, «пояснення» є наближеним, тому що на норму прибутку акції впливає ряд інших чинників, окрім загальної ситуації на біржі, що виражається нормою при­бутку ринкового показника чи ринкового портфеля. Дію інших чинників відображає випадкова складова рівняння регресії (е_i). Власне, введення цієї випадкової величини дозволяє поставити знак рівності між лівою і правою частинами рівняння.

Дуже важливу роль у цьому рівнянні відіграє коефіцієнт β_i (в економічній науці та практиці його називають коефіцієнтом бета).

Йому можна дати наступну інтерпретацію: коефіцієнт бета звичайної акції вказує, на скільки відсотків наближено зросте (знизиться) норма прибутку акції, коли норма прибутку ринку зросте (знизиться) на 1%. Тобто, це означає, що коефіцієнт бета певної акції показує, в якій мірі норма прибутку акції реагує на зміни, що відбуваються на ринку в цілому. Як від­значається в другому розділі, коефіцієнт бета може трактуватися як міра ринкового ризику певної акції.

Наведемо кілька простих прикладів.

Коефіцієнт бета дорівнює нулеві (β_i = 0). Це означає, що норма прибутку даного цінного паперу ніяк не реагує на зміни на ринку. Тобто, даний цінний папір не обтяжений ринковим ризиком. Таким папером може бути, зокрема, державна облі­гація, для котрої норма прибутку майже позбавлена ризику.

Величина коефіцієнта бета така, що 0 < β_i < 1. Це означає, що норма прибутку даної акції досить помірковано реагує на зміни, що відбуваються на ринку цінних паперів, таку акцію називають дефенсивною (захищеною) акцією.

Коефіцієнт бета дорівнює одиниці (β_i = 1). Це означає, що норма прибутку даної акції змінюється так само як і норма прибутку ринку. Зауважимо, що ринковий портфель має кое­фіцієнт β = 1.

Величина коефіцієнта бета більша ніж одиниця (β_i > 1). Це означає, що норма прибутку акції значною мірою залежить від змін, що відбуваються на ринку. Таку акцію називають агресивною.

В Україні останнім часом починають в періодичних виданнях публікувати дані про це, але досить нерегулярно. В країнах з розвинутою ринковою економікою ряд солідних часописів систематично публікують коефіцієнт бета для багатьох акцій. Більшість акцій Нью-Йоркської біржі мають коефіцієнт бета, який знаходиться в інтервалі від 0,5 до 1,5.

Приклад.Маємо акцію, характеристична лінія котрої подана наступним рівнянням:

m_i = 3,1 + 1,3m_M + е_i.

Наведене рівняння показує, що зміна ринкового (біржового) показника на 1% призводить до зміни норми прибутку даної акції приблизно на 1,3%. Тобто, ця акція значно реагує на зміни на ринку цінних паперів.

Характеристична (ринкова) лінія акції може бути проілюст­рована графічно (рис. 4.9).

На рис. 4.9 зображена характеристична лінія даної акції, де на осі абсцис відкладаються норми прибутку ринку, а на осі ординат норми прибутку даної акції. Коефіцієнт бета відповідає тангенсу кута „α” нахилу характеристичної лінії акції до осі абсцис. Отже, чим більшу величину має „β” акція, тим більшим є кут нахилу характеристичної лінії. Збільшення коефіцієнта „β” означає збільшення ступеня реагування норми прибутку акції на зміни норми прибутку ринкового показника.

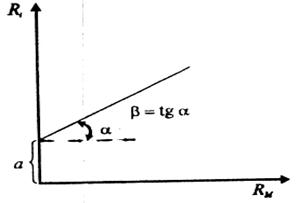
Рис. 4.9. Ринкова лінія акції

Важливою проблемою є визначення характеристичної лінії акції. Існує декілька способів цього. Найчастішим є використання інформації за минулі періоди та широко відомого методу най­менших квадратів.

У випадку застосування методу найменших квадратів (не вдаючись в деталі) одержимо наступні рівняння для визначення коефіцієнтів аi та β:

;

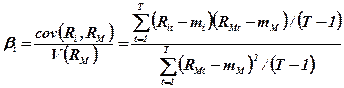a_i = m_i – β_im_M,

де cov (R_i, R_M) – коваріація між i-ю акцією і нормами прибутку ринку; V(R_M) – варіація (дисперсія) ринкової норми прибутку цінних паперів; Т – кількість періодів, за які береться відповідна інформація; R_it - норма прибутку i-i акції в t-му періоді; R_Mt – норма прибутку показника ринку (індексу біржі) в t-му періоді; m_i – сподівана норма прибутку i-ї акції; m_M – сподівана ринкова норма прибутку.

У даному випадку

;

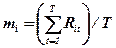Метод найменших квадратів дозволяє визначити також варіа­цію (дисперсію) ринкової норми прибутку і варіацію (дисперсію) випадкової складової.

Визначаються вони за допомогою таких формул:

;

;

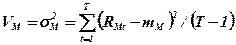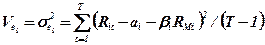де V_M = σ_M² – варіація показника ризику; 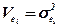- варіація випадкової складової, яка відповідає i-й акції.

Отже, робимо висновок, що:

1) для обчислення норми прибутку i-й акції необхідно мати коефіцієнт "a_i" коефіцієнт "β_i" цієї акції, а також сподівану (середню арифметичну) норму прибутку ринку;

2) для обчислення ризику i-й акції необхідно знати коефіцієнт "β_i", варіацію, пов'язану з ринком в цілому, а також варіацію випадкової складової, що відповідає даній акції;

3) для обчислення коефіцієнта кореляції i-й та j-ї акцій необхідно знати коефіцієнти "β_i" і "β_j", варіацію ринкового показника, а також середньоквадратичні відхилення i-ї та j-ї акцій.

Частку систематичного ризику в загальному ризику i-й си­туації можна подати за допомогою коефіцієнта z_i, що обчис­люється за формулою:

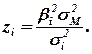
Велика частка систематичного ризику в загальному ризику певної акції вказує, зокрема, на те, що поводження ринку цінних паперів має великий вплив на ризик, яким обтяжена дана акція. І, навпаки, мала частка свідчить про те, що лінійна регресійна залежність між нормами доходу певної акції та ринку не досить добре характеризує цю залежність тощо.

Поняття систематичного ризику (ризику ринку) і специфічного ризику має безпосередній зв'язок з диверсифікацією, з формуванням портфеля цінних паперів. Диверсифікація призводить до зниження ризику портфеля стосовно окремих цінних паперів, що залучені до нього. Однак, ризик портфеля далеко не завжди можна зробити рівним нулеві (якщо цей портфель не порожній чи не сформований лише з безризикових цінних паперів).

Вміла методика формування портфеля дозволяє суттєво знизити (позбавитися) специфічний ризик, яким він обтяжений. Однак залишається ще ризик ринку, котрий може мати певний (більший чи менший) ступінь в складі всіх акцій, що залучені до портфеля, вилучити котрий не вдається шляхом диверсифікації.

Викладені вище засади класичної моделі мають широке застосування. Коефіцієнти "β" використовують під час прийняття рішень у фірмах. Вони придатні при обчисленні ціни необ­хідного капіталу для інвестиційних програм.

Коефіцієнти β означені вище як міра систематичного ризику окремих акцій (майнових активів).

Нехай розглядається портфель із "n" акцій (різних активів), часки яких у портфелі складають відповідно х_i, 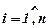, а також відомі коефіцієнти β_i,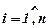

Можна довести, що коефіцієнт бета портфеля (β_р) розраховується за формулою:

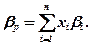
Необхідно зазначити: якщо певну фірму трактувати як множину окремих груп активів, то, користуючись викладеним вище, можна обчислити, зокрема, вплив інвестиційних проектів на коефіцієнт "β" фірми в цілому. А, отже, на систематичний ризик, ціну власного капіталу, а також середньозважену ціну капіталу. Параметри ці мають вирішальний вплив на результати обчислення економічної ефективності інвестиційних проектів та відповідних рішень.

Читайте також:

1. CMM. Модель технологічної зрілості. Зрілі і незрілі організації.
2. G2G-модель електронного уряду
3. I. ІСТОРИЧНІ ШЛЯХИ ФОРМУВАННЯ УКРАЇНСЬКОЇ КУЛЬТУРИ
4. OSI - Базова Еталонна модель взаємодії відкритих систем
5. V – модель
6. XIII. Формування та оприлюднення рейтингового списку вступників, рекомендованих до зарахування
7. Абстрактна модель
8. Абстрактна модель
9. Абстрактна модель оптимального планування виробництва
10. АДАПТОВАНА ДО РИНКУ СИСТЕМА ФОРМУВАННЯ (НАБОРУ) ОКРЕМИХ КАТЕГОРІЙ ПЕРСОНАЛУ. ВІДБІР ТА НАЙМАННЯ НА РОБОТУ ПРАЦІВНИКІВ ФІРМИ
11. Алгоритм формування комплексу маркетингових комунікацій
12. Алгоритм формування потенціалу Ф2

Переглядів: 765