• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Загальні засади та концепція теорії корисності.

Для задач прийняття рішень за умов невизначеності та ризику принцип оптимальності нерідко будується у виді функції корисності. Оскільки при наявності ризику результати рішень залежать від випадкових величин, то для порівняння їх ефективності необхідно вміти порівнювати функції розподілу ефективності. У цьому випадку важливе значення для прийняття рішень мають результати про властивості функції корисності чи конкретного її виразу, які витікають із того чи іншого набору властивостей співвідношень пріоритетності.

Корисність визначає ступінь задоволення, яке одержує суб'єкт від споживання товару чи виконання будь-якої дії.

Можливо, що найбільш загальний підхід щодо оцінки ступеня (міри) ризику полягає у введенні функції корисності. Концепція функції корисності є одним із важливих елементів будь-якої сучасної економічної теорії. Вона дозволяє здійснити співвимірність споживчих елементів різних товарів.

Корисність включає важливу психологічну компоненту, тому що люди досягають корисності, отримуючи речі, що приносять їм задоволення. В економічному аналізі корисність часто використовується для того, щоб описати пріоритет в процесі ранжування наборів споживчих товарів та послуг. Якщо людина більше задоволена від купівлі декількох книжок, ніж від придбання сорочки, то книжки мають для цієї людини більшу корисність, ніж сорочка. Сумірність цінних паперів, котрі також є товаром, на перший погляд, простіше здійснити, оскільки усі вони мають ціну. Але ризиковані цінні папери — це документи, що свідчать про можливість одержання грошей у майбутньому, і тут сумірність проблематична: не можна сказати, котра з величин випадкова, якою є ефективність (норма доходу) кожного з цінних паперів, буде більшою чи меншою, а отже, не можна сказати, який з цінних паперів чи який портфель цінних паперів є пріоритетнійшим.

Встановлення будь-якої міри ризику є спробою подолати це протиріччя, характеризуючи випадкову величину одним показником (параметром). Застосовуючи різні функції корисності, можна описати будь-які варіанти оцінки випадкової економічної ситуації у виді сподіваного значення такої функції. Природа, що будь-які підходи такого роду є суб'єктивними, але без них не обійтися, якщо намагатися ввести певну єдину міру.

Існує таке поняття як пріоритет, яке досить часто використовується менеджерами (суб'єктами прийняття рішень).

Позначимо співвідношення «більш пріоритетніше ніж”, «байдуже», «не гірше ніж» відповідно символам , ~, .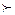

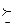Нестроге співвідношення пріоритетності «не гірше ніж» є одним із основних найпростіших понять; його записують так:

х 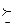у,

де х та у є набором товарів чи послуг (точками простору Х).

Цей запис означає, що певний суб'єкт (споживач) вважає для себе набір х або пріоритетнійшим, ніж набір у, або не робить між ними різниці, тобто х не гірше ніж у. Можна визначити поняття байдужості та строгої пріоритетності у термінах нестрогого співвідношення пріоритетності: набори товарів х та у байдужі (еквівалентні) для споживача (х~ у) тоді і лише тоді, коли

(х 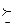у та у 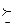х).

А коли ж споживач бажає обрати х, а не у, тобто х пріоритетніше, ніж у (записують х 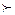у), тоді і лише тоді, якщо він не гірше ніж у, а у гірше, ніж х. Значить х 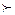у тоді та лише тоді, коли

х 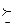у, а у 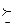х – несправедливе.

Надалі будемо вважати, що нестроге співвідношення пріоритетності задовольняє дві основні аксіоми.

Перша аксіома стверджує, що це співвідношення є досконалоюнапівупорядкованістю у просторі товарів X. Співвідношення називається досконалим, якщо для двох заданих наборів х та у з X справедливе одне з двох співвідношень:

х 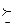у, або у 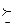х, або одночасно.

Це означає, що у просторі товарів немає таких «білих плям», де пріоритет не існує. Співвідношення називають частковою впорядкованістю, якщо воно транзитивне, тобто для трьох заданих наборів х, у та z iз X виконується умова:

якщо х 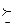у, та у 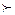z, то х 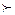z,

що виражає сумісність пріоритетів, і, якщо співвідношення рефлексивне, тобто для будь-якого 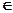х Х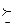

х х.

Цей факт випливає з досконалості співвідношення. Нестроге співвідношення пріоритетності є досконалою частковою впорядкованістю простору товарів і означає, що співвідношення байдужості є співвідношенням еквівалентності, котре транзитивне, оскільки при заданих х, у та z 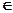Х, якщо

х ~ у та у ~ z, тоді х ~ z

рефлексивне, оскільки при заданому 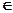х Х

х ~ х,

та симетричне, оскільки при заданих х та у 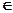Х

х ~ у означає у ~ х.

Для доведення, наприклад, транзитивності зазначимо, що х ~ у та у ~ zозначає з визначення байдужості, що х 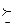у та у 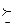z і що z 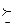х и у 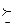х. Тоді з транзитивності нестрогого співвідношення пріоритетності х 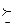z та z 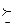х випливає, що х ~ z.

Співвідношення байдужості, як співвідношення еквівалентності, ділить простір товарів Х на класи еквівалентності — підмножини, що попарно не перетинаються, називаються множинами байдужості, кожна з яких складається з усіх наборів, байдужих заданому наборові х:

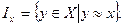
Друга основна аксіома стверджує, що нестроге співвідношення пріоритетності неперервне, тобто пріоритетні множини, кожна з яких складається з усіх наборів, що епріоритетніші чи байдужі заданому наборові х:

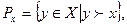
і непріоритетні множини, кожна з яких складається з усіх таких наборів, для котрих заданий набір х пріоритетніший чи байдужий

є замкнутою множиною простору товарів для будь-якого 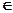х Х.

За цією аксіомою обидві множини містять усі граничні точки, причому для обох множин ці точки утворюють множину байдужості I_x, рівну перетинові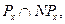

З цих основних аксіом досконалої нестрогої впорядкованості та неперервності випливає, що існує неперервна дійсна функція, визначена на елементах множиш X - U(·), котру називають функцією корисності і для якої

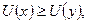якщо х 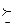у.

Функція корисності співставляє кожному наборові споживчих товарів певне число в такий спосіб, що, якщо набір А пріоритетніший, ніж набір В (А 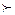В), то число, яке відповідає набору А, буде більшим, ніж те, що відповідає набору В.

Гранична корисність вимірює додаткове задоволення, яке одержує особа від споживання додаткової кількості товару.

Наприклад, гранична корисність, що пов’язана з зростанням споживання від 1 до 5 одиниць шоколаду, може дорівнювати 10, від 6 до 10 одиниць — 5, а від 11 до 15 одиниць — 3. Ці цифри узгоджуються з принципом зниження граничної корисності. У міру зростання споживання товару процес додаткового споживання дає усе менший приріст корисності.

2.Корисність за Нейманом. Сподівана корисність.

Для визначення корисності розглянемо вибір особи за умов ризику, який формалізується за допомогою поняття лотереї.

Для цього необхідно з множини пред’явлених експертам значень певного економічного показника (об’єкта) виділити два х_* и х^* таких, що х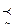_* х для всіх х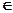_* Х та х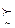^* х для всіх х 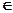Х, тобто найменш пріоритетне, в певному сенсі, значення економічного показника (це буде «нуль» даної шкали інтервалів) і найбільш пріоритетне у певному сенсі значення показника (разом з «нулем» воно визначить масштаб даної шкали). Власне так побудована функція корисності Дж. Неймана і О. Моргенштерна. Експерту пропонують порівнювати альтернативу:

1) значення показника х;

2) лотерею: одержати х^* з імовірністю (1 - р) чи х_* з імовірністю (р). Величину імовірності р змінюють доти, доки, на погляд експерта, значення показника х і лотерея L (х^*, р, х_*) не стануть еквівалентними. Максимальному та мінімальному значенням х^* та х_* приписують довільні числові значення U^*= U(х^*) та U_*= U(x_*), але так, щоб U^* > U_*.

Пiд лотереєю L (х_*, р(х), х^*) розуміють ситуацію, в якій особа може отримати х_* з імовірністю р(х) або х^* з імовірністю 1 - р(х).

Корисність варіанту х визначається ймовірністю р(х), при якій особі байдуже, що обирати: х — гарантовано, чи лотерею L (х_*, р(х), х^*), де х^*, х_* — вектори, більш та менш пріоритетні порівняно з х.

Нехай L — лотерея, що призводить до виграшів (подій) х₁,х₂,....х_n з відповідними ймовірностями р₁, p₂, ….р_N. Позначимо сподіваний виграш (математичне сподівання виграшу) через х.

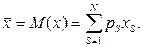
Справедлива головна формула теорії сподіваної корисності

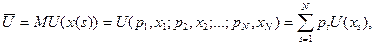
тобто корисність ансамблю результатів збігається математичним сподіванням корисності результатів.

Поняття детермінованого еквівалента лотереї L є одним з основних при розгляді різних характеристик ризику і їх взаємозв'язку з функціями корисності.

Детермінований еквівалент лотереї L – це гарантована сума 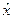, отримання якої еквівалентне участі в лотереї, тобто 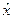~ L. Отже 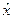визначається з рівняння:

U(x) = M [U(x)], або 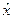= U^-1MU(x)

Сподіваний виграш та детермінований еквівалент, які визначені згідно з наведеними формулами, стосуються лотереї з кінцевим числом можливих виграшів. Якщо можливі виграші описуються щільністю розподілу φ(х), то сподіваний виграш у цій лотереї дорівнює

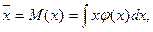
а детермінований еквівалент 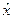є розв’язком рівняння:

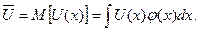
Згідно з теорією сподіваної корисності, суб’єкт керування, що приймає рішення за умов невизначеності та ризику, повинен максимізувати математичне сподівання корисності результатів. Отже, якщо f(x, ω) – вектор результатів, що залежать від вектора плану х та елементарної події ω, то ефективність плану х для значень ω, які містяться у множині Ω, ω 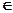Ω з імовірнісною мірою Р(dω), має вид

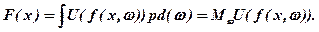
Величина Р(dω) визначається або за статистичними методами при наявності необхідної кількості спостережень, або за допомогою спеціальних експертних процедур.

Читайте також:

1. I. Загальні збори АТ
2. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
3. I. Загальні положення
4. II. ЗАГАЛЬНІ ПОЛОЖЕННЯ.
5. XXXIII. ЗАГАЛЬНІ ПРОФЕСІЇ (У ВСІХ ГАЛУЗЯХ ГОСПОДАРСТВА)
6. А .Маршалл - основоположник неокласичної теорії.
7. А) загальні критерії
8. Абстрактна небезпека і концепція допустимого ризику.
9. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
10. Альтернативні теорії вартості
11. Альтернативні теорії вартості
12. Альтернативні теорії вартості

Переглядів: 434