• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Різне ставлення до ризику та корисність.

Особу, яка приймає рішення, називають несхильною до ризику, якщо для неї більш пріоритетною є можливість отримати гарантовано сподіваний виграш у лотереї, ніж приймати в ній участь.

З попереднього відомо, що корисність лотереї збігається з математичним сподіванням корисності її випадкових результатів. Отже умова несхильності до ризику приймає вид

U (M [x (ω)]) > M [U (x (ω))],

де М( ) – символ (оператор) математичного сподівання, х – випадкова величина, що залежить від елементарної події ω.

Для зростаючих функцій корисності премією π(х) за ризик в лотереї L є різниця між сподіваним виграшем та детермінованим еквівалентом

π(х) = М [x (ω)] - .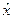

Страховою сумою (СС) називають величину детермінованого еквіваленту з протилежним знаком, тобто

CC(x) = - 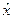= -U^-1 (M [U (x (ω))].

Умова схильності до ризику має вид

U (M [x (ω)]) < M [U (x (ω))].

Умова байдужості до ризику має вид

U (M [x (ω)]) = M [U (x (ω))].

Приклади функцій корисності:

1) зростаюча функція корисності для суб'єкта керування байдужого до ризику

U(x) = a + bx, b > 0;

2) зростаюча функція корисності для суб'єкта керування несхильного до ризику

U(x) = log (x + b), x > - b;

3) зростаюча функція корисності з несхильністю до ризику

U(x) = a – be^-cx, b > 0, x ≥ 0;

4) зростаюча функція корисності зі схильністю до ризику

U(x) = x², x ≥ 0.

За своєю фізичною сутністю премія за ризик (надбавка за ризик) — це сума (в одиницях виміру критерію х, якою суб’єкт керування (особа, що приймає рішення) згоден знехтувати (поступитися нею) з середнього виграшу (тобто ця сума менша, ніж математичне сподівання виграшу) за те, щоб уникнути ризику пов'язаного з лотереєю.

Якщо особа, що приймає рішення зіштовхується з несприятливою для неї лотереєю (тобто лотереєю, що менш пріоритетна ніж стан, в якому вона у даний момент знаходиться), то природно виникає питання, скільки вона заплатила б (в одиницях виміру критерію х) за те, щоб не брати участі у цій лотереї (уникнути її).

На рис. 5.1 показано, як графічно можна зобразити ставлення особи до ризику. Крива ON, що задає рівень корисності (на осі ординат), котрий може бути досягнутий за відповідним рівнем доходу (відкладеного в тис. грн. на осі абсцис). Ця крива ілюструє несхильність особи до ризику.

Рис. 5.1. Функція корисності особи, що несхильна до ризику

Міра несхильності до ризику.Локальна несхильність до ризику у деякій точці х визначається за допомогою функції несхильності:

r(x) = -U"(x)/U'(x).

Використовують також формулу:

r(x) = -(d/dx) [log U'(x)].

Читайте також:

1. Абстрактна небезпека і концепція допустимого ризику.
2. Аналiз ризику методами iмiтацiйного моделювання
3. Аналіз втрат від маркетингового ризику
4. Аналіз кредитного ризику банку
5. Аналіз невизначеності і ризику
6. Аналіз ризику в життєдіяльності людини.
7. Аналіз ризику можливих збитків
8. Аналіз ризику через моделювання.
9. Аналіз ризику.
10. Аналіз та оцінка інвестування в умовах ризику. Якісні та кількісні методи оцінювання проектних ризиків.
11. В. І. Ленін про ставлення до Всеукраїнської вчительської спілки. (З виступу 3 грудня 1919 р.)
12. Взаємодія важелів. Оцінка сукупного ризику, зв'язаного з підприємством.

Переглядів: 751