• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Функція корисності з інтервальною нейтральністю.

Функція корисності з інтервальною нейтральністю відображає відношення до ризику особи, що приймає рішення за умов, коли результат знаходиться в певних межах. Якщо йдеться про весь інтервал змінення результатів, корисність якого оцінюють, то тут відношення до ризику не буде нейтральним.

Один із типів функції з інтервальною нейтральністю до ризику має такий вид.

U(x) = min (a_ix + b_i).

Якщо a_i> 0, то U(x) – зростаюча функція корисності, що характеризує несхильність до ризику, оскільки вона є опуклою вгору (рис. 5.4).

Рис. 5.4. Інтервальна нейтральність (глобальна несхильність) до ризику

Часто U(х) представляють у виді:

a₁х + b₁, 0 ≤ x ≤ x₁,

a₂x + b₂, x₁ ≤ x ≤ x₂,

U(x) =

a_nx + b_n, x_{n 1} ≤ x ≤ ∞.

де a₁>a₂ ……… > a_n, a b₁ < b₂ < b_n, x₁, x₂, x_n-1 – точки перетину графіків функцій a₁x + b₁ та a₂x +b₂, a₂x +b₂таa₃x + b₃ і т.д. Оскільки будь-який з доданків корисності не змінює її стратегічну еквівалентність, приймають b₁=0.

На інтервалах [0, х₁], [х₁, х₂], , [х_n-1, ∞] функція буде нейтральною до ризику.

За допомогою функцій з iнтервальною нейтральністю до ризику можна з будь-якою точністю апроксимувати нелінійні функції корисності.

Для зручності інтервали нейтральності до ризику класифікують. Наприклад, інтервал [0,х₁], зображений на рис. 5.4, є інтервалом з високою граничною корисністю, [х₁, х₂] — з середньою, [х₂, ∞] - з низькою.

Функції інтегрально-нейтральні до ризику в багатьох випадках дають можливість перейти до лінійних залежностей. Нехай виникає потреба в максимізації функцій корисності U(x) = min (a_ix + b_i):

U(x) = 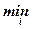(a_ix + b_i) → ,

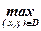де у — вектор параметрів деякої системи; D — множина допустимих пар (х,у).

Вважається, що ця задача еквівалентна задачі з лінійною функцією корисності:

U → 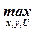; U ≤ a_ix + b_i; (i = 1, n; (x,y) 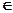D).

Якщо вектор результатів f складається з одного елемента (одноцільова задача), то відношення до ризику суб'єкта керування можна описати за допомогою функції корисності U(f). Існує досить багато конкретних типів функцій корисності.

Розглянута функція з інтервальною нейтральністю до ризику U(f) = 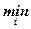(a_if + b_i), де a₁ > a₂ > … > a_n та 0 ≤ b₁ < b₂ ,< … < b_n відображає глобальну несхильність до ризику на окремих інтервалах.

Функція U(f) = 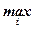(a_if + b_i), де 0 < a₁ < … < a_n та 0 ≥ b₁ > b₂ > … > b_n,відображає глобальну схильність до ризику.

Читайте також:

1. V теорія граничної корисності визначає вартість товарів ступенем корисності останньої одиниці товару для споживача.
2. Атрибутивна функція ґерундива
3. Б) Поняття корисності: (поняття, гранична та сукупна корисність продукту).
4. Багатомірність і сутність культури виявляється в її основних функціях: соціальній (гуманістичній), пізнавальній, аксиологічній, семіотичній, нормативній.
5. Базовою для інтегрального числення є така теорема: ТЕОРЕМА 2. Якщо функція неперервна, то для неї існує
6. Бюджетування як функція фінансового контролінгу
7. Виробництво та виробнича функція
8. Виробництво та виробнича функція
9. Виробництво та виробнича функція
10. Виробнича функція
11. Виробнича функція з двома змінними факторами
12. Виробнича функція з двома змінними факторами

Переглядів: 1746