• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Чистий вигин криволінійного бруса. Задача Головіна

При чистому згинанні криволінійного бруса, вісь якого обкреслена по дузі окружності (рис. 4.13), розподіл напружень у всіх радіальних перерізах однакове. Отже, напруження в такому брусі можна визначати по формулах (4.40).

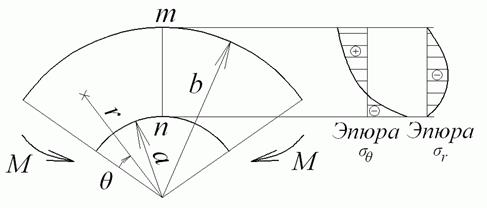
Рис. 4.13. Чисте згинання криволінійного бруса

Для визначення вхідних у ці формули постійних маємо наступні умови на криволінійних поверхнях:

при	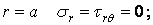(а)
при	(б)

На торцях рівнодіюча зусиль повинна бути дорівнює нулю, тобто

,

(в)

і тому ці зусилля повинні приводитися до пари з моментом :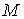

.

(г)

Умови (а) і (б) для дотичних напружень виконуються тотожно, а відносно нормальних напружень після підстановки першої формули (4.40) приводяться до наступних рівнянь:

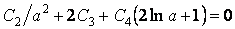;	(д)
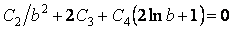.	(е)

Умова (в) приймає наступний розгорнутий вид:

,

звідки після інтегрування

.

(ж)

Аналогічно з умови (г) у вигляді

після інтегрування одержуємо

.

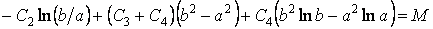Неважко бачити, що при виконанні умов (д) і (е) умова задовольняється тотожно. Вирішуючи спільно рівняння (д), (е) і (з), одержуємо:

;

.

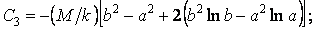
Тут введене позначення:

.

Підставляючи отримані постійні у формули (4.40), знаходимо

(4.41)

Епюри напружень і 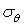побудовані на рис. 4.13.

Точне рішення задачі про чисте згинання, а також задача про поперечне згинання криволінійного бруса вперше отримане в 1881 р. X. С. Головіним.

Порівнюючи формули (4.41) і (3.23), зауважуємо, що на відміну від прямого бруса при чистому згинанні криволінійного існує тиск волокон один на одного. В опорі матеріалів рішення задачі чистого згинання криволінійного бруса засновано на гіпотезі плоских перерезів і допущенні про відсутність тиску поздовжніх волокон один на одного. При цьому виходять наступні результати:

(4.42)

де 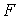— площа поперечного переріза; — відстань від центра ваги перерізу до нейтральної осі; — середній радіус кривизни бруса.

У табл. 4.1 наведені результати обчислення напружень по формулах (4.41) і (4.42) для бруса великої кривизни, коли висота перерізу 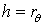або радіус 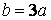. Найбільше значення напруження 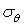, отримане методом теорії пружності, прийнято за одиницю.

Таблиця 4.1

Порівняння результатів теорії пружності та опору матеріалів

Формули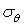
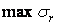
при	при
Теорії пружності (4.41)	–1,000	0,492	–0,192
Опору матеріалів (4.42)	–1,005	0,480
Розбіжність, %	0,5	2,5	--

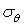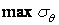Як видно з таблиці, навіть при дуже великій кривизні бруса рішення опору матеріалів відносно нормального напруження відрізняється всього на 2,5% від точного рішення. Максимальні нормальні напруження становлять 19,2% від , однак вони виникають у точках, де напруження 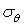близькі до нуля, і, отже, не мають значення при оцінці міцності. Тому при розрахунку криволінійних брусів рішення опору матеріалів цілком прийнятно.

Читайте також:

1. Антисептики ароматичного ряду (фенол чистий, іхтіол, дьоготь, мазь Вількінсона, лінімент за Вишневським). Особливості протимікробної дії та застосування.
2. Б. Задача
3. Валовий національний дохід і чистий національний дохід
4. Взаємне положення площин. Перша позиційна задача
5. Взаємне положення прямої і площини. Друга позиційна задача.
6. Вторая задача анализа на чувствительность
7. Головна задача м/н фінансового менеджменту полягає у оцінці короткострокових і довгострокових активів і зобов’язань фірми у часовому і просторовому використанні м/н ринків.
8. Двоїста задача
9. Двухмерная задача Коши
10. З праці В. Леніна «О задачах пролетариата в данной революции»
11. Загальна задача лінійного програмування (ЗЛТ)
12. Задача # 12 (з тих, що вона скидувала)

Переглядів: 627