• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Поняття про дію зосередженої сили на пружний півпростір

Пружним півпростором називається частина простору, обмежена площиною. Задача про дію сили , прикладеної по нормалі до цієї площини (рис. 4.16), ставиться до просторової задачі теорії пружності і є більш складною, чим задача про дію сили на границі напівплощини (див. 4.6). Її рішення зручно будувати в циліндричній системі координат.

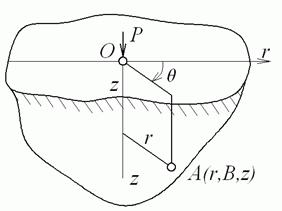
Рис. 4.16. Дія сили на пружний півпростір

У цій системі будь-яка точка простору визначається трьома координатами , , . Задача є осесимметричною, тому всі перерізи, паралельні площини , перебувають в однакових умовах і всі функції не залежать від полярного кута .

Рішення розглянутої задачі належить Ж. Буссінеску. Інтегрування системи диференціальних рівнянь рівноваги й рівнянь нерозривності деформацій Бельтрамі - Мітчелла в циліндричній системі координат дає наступний результат:

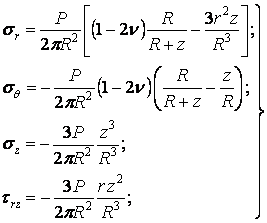
(а)

де як і раніше 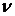— коефіцієнт Пуассона, a .

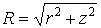Напружений стан, описуваний формулами (а), зображене на рис. 4.17. З формул треба, що на будь-якій прямій напруження обернено пропорційні квадрату відстані від початку координат .

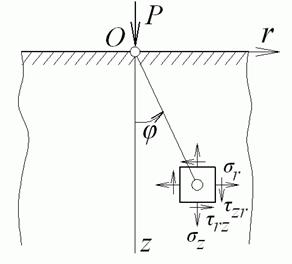
Рис. 4.17. Рішення Ж. Буссінеска

Рішення, як і в плоскої задачі, має особливість на початку координат, тому для включення в нього сили зроблена її заміна статично еквівалентним навантаженням, що розподілене по сфері малого радіуса 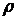, обкресленої з початку координат. На підставі принципу Сен-Венана така заміна позначиться на розподілі напружень тільки поблизу початку координат.

На горизонтальній площадці в довільній точці 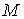(рис. 4.18) відношення напружень

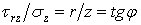
і, отже, напрямок повного напруження на цій площадці 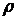проходить через початок координат . Величина цього напруження

.

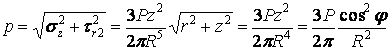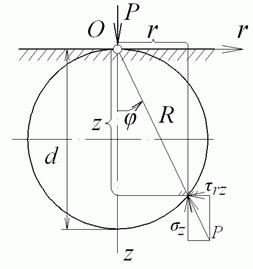
Рис. 4.18. Напруження на горизонтальній площадці

Якщо накреслити сферу діаметром , що проходить через точку і касається границі площини на початку координат (рис. 4.18), то

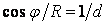
і повне напруження

.

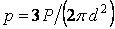Таким чином, у всіх точках розглянутої сфери повне напруження на горизонтальних площадках постійне.

Для визначення переміщень у півпросторі необхідно напруження (а) підставити у формули закону Гука, виражені в циліндричній системі координат, і знайти деформації. Потім треба проінтегрувати геометричні співвідношення Коші в циліндричній системі координат, у результаті чого одержимо наступні складові переміщень:

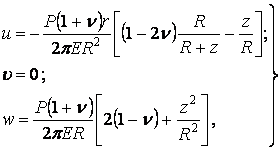
(б)

де 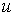— радіальна складова переміщення; 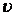— окружна, а — переміщення уздовж осі .

З формул (б) треба, що на будь-якій прямій переміщення обернено пропорційні відстані від початку координат і при 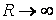прагнуть до нуля.

Найбільший інтерес представляють вертикальні переміщення точок на граничній площині (при )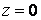

.

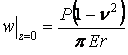Ця формула справедлива у всіх точках, за винятком малої області в початку координат.

Рішення, отримане для зосередженої сили, можна поширити на навантаження, розподілене по деякій площі граничної площини.

Читайте також:

1. II. Поняття соціального процесу.
2. V. Поняття та ознаки (характеристики) злочинності
3. VII. Поняття про рану, рановий процес, види загоювання ран
4. А/. Поняття про судовий процес.
5. Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
6. Адміністративний проступок: поняття, ознаки, види.
7. Адміністративні провадження: поняття, класифікація, стадії
8. Акти застосування юридичних норм: поняття, ознаки, види.
9. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
10. АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ
11. АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ
12. Аудиторські докази: поняття та процедури отримання

Переглядів: 499