• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Задання та запис множин

Для задання множини, утвореної з будь-яких елементів, будемо використовувати такі способи. В основі всіх способів лежить позначення множини за допомогою фігурних дужок.

СПОСІБ 1. Якщо a₁, a₂, ..., a_n – деякі об’єкти, то множину цих об’єктів можна позначити через {a₁, a₂, ..., a_n}, де у фігурних дужках перелічують всі елементи відповідної множини. Таким способом переважно задають скінченні множини, які мають невелику кількість елементів. Порядок запису елементів множини при цьому позначенні є неістотним. Якщо множина містить однакові елементи, то у фігурних дужках їх прийнято записувати лише один раз.

Наприклад, множину десяткових цифр записуюєть {0,1,2,3,4,5,6,7,8,9}, множину основних арифметичних операцій – {+,-,*,/} або {*,/,+,-}, множину розв’язків нерівності x² +1£ 1 – {1}.

СПОСІБ 2. Цей спосіб задання множин ґрунтується на описі загальної характеристичної властивості (умови) для всіх об’єктів, що утворюють множину.

У загальному випадку задання множини M має вигляд:

M = {a | P(a)}.

Цей вираз читається так: “множина M – це множина всіх таких елементів a, для яких виконується властивість P”, де через P(a) позначено властивість, яку мають елементи множини M і тільки вони. Іноді замість вертикальної риски записують двокрапку.

Наприклад,

S = { n | n - непарне число }

X = { x | x = pk, kÎZ},

F = { f_i | f_i+2 = f_i+1 + f_i, iÎN, f₁ = f₂ = 1 }.

Порожню множину можна визначити за допомогою будь-якої суперечливої властивості, наприклад: Æ={x | x¹x} тощо. Твердження “множина M – не порожня” можна замінювати рівносильним йому твердженням “існують елементи, які належать множині M”.

СПОСІБ 3. Елементи множини можна задати за допомогою елементів вже відомих множин із застосуванням для них деякого правила чи операцій над вже відомими множинами. При цьому задання множини повинно обов’язково містити опис допоміжних (вже відомих) множин.

Наприклад,

N₀={0, N}, N ={1, 2, 3, 4, 5, …};

N_2n= { 2n | n=1, 2, 3, …} – множина всіх парних натуральних чисел;

X = { x | x = pk, kÎZ},

Останнім способом задано множину всіх можливих пар, перша компонента яких належить множині 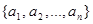, а друга – .

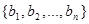Отже, після вертикальної риски слід записати опис допоміжних множин.

Читайте також:

1. А. Розрахунково-пояснювальна записка
2. Алгебра множин
3. Аналіз паралельного інтерейсу з DSP-процесорами: запис даних в ЦАП, що під’єднаний до адресного простору пам’яті
4. Бухгалтерські записи (проводки) складають перед записом сум на рахунки.
5. Бухгалтерські записи (проводки) – прості та складні.
6. Бюджетні множини й лінії бюджетного обмеження
7. В крайньому випадку, записи мають бути тезисні, в які ви можете заглянути у крайньому випадку (при загрозі краху, загибелі тощо).
8. Валютна позиція банку та її врахування в бухгалтерських записах за операціями в іноземній валюті
9. Види відображень множин
10. Визначення добутку двох цілих невід’ємних чисел як числа елементів декартового добутку двох скінченних множин
11. Визначення добутку на множині цілих невід’ємних чисел, його існування та єдиність. Операція множення та її основні властивості (закони).
12. Визначення загальної множини компонентів

Переглядів: 914