
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 5. Арифметичні операції в двійково-десяткових СЧ
5.1 Представлення десяткових чисел в Д-кодах
5.2 Формальні правила порозрядного складання в Д-кодах
5.3 Представлення від’ємних чисел в Д-кодах
5.4 Виконання операцій додавання і віднімання чисел в Д-кодах
5.1 Представлення десяткових чисел в Д-кодах
Операції над десятковими числами (десяткова арифметика) часто включається в склад головних команд універсальних ЄВМ. Крім того десяткова арифметика застосовується широко в електронних калькуляторах і персональних мікроЄВМ. Тому крім загальної інформації про можливості представлення десяткових чисел розробнику потрібно знати і алгоритми виконання арифметичних операцій.
Д*код (двійково-кодоване представлення) десяткового числа – таке його представлення в якому кожна десяткова цифра зображується тетрадою з двійкових символів :
 =
=  (5.1)
(5.1)
де 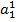 – двійкові розряди тетроди j: n – кількість десяткових розрядів.
– двійкові розряди тетроди j: n – кількість десяткових розрядів.
Кількість різних Д кодів визначається кількістю можливих поєднань по 10 з 16 комбінацій, які допускає тетрада. При обробці Д-кода слід виходити з загальних вимог представлених до систем числення:
− різним десятковим цифрам повинні відповідати різні тетради;
− велика десяткова цифра повинна зображуватися великою тетрадаю (якщо розряди тетради мають мають вагу по двійковій системі числення);
− для десяткових цифр a = {  } і b = {
} і b = { 


 }, пов’язаних відношенням a + b = 9, повинно задовольнятися умовою
}, пов’язаних відношенням a + b = 9, повинно задовольнятися умовою
β = 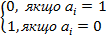 ( і = 1, 2, 3,4) (5.2)
( і = 1, 2, 3,4) (5.2)
Для однозначності переводу чисел в Д-код і назад бажано, щоб розряди тетрад мали певну вагу. Тоді значення десяткової
цифри 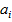 відповідає виразу
відповідає виразу

де 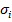 − вага розряду тетради .
− вага розряду тетради .
В табл. 5.1 представлено кодування десяткових цифр в різних Д-кодах.
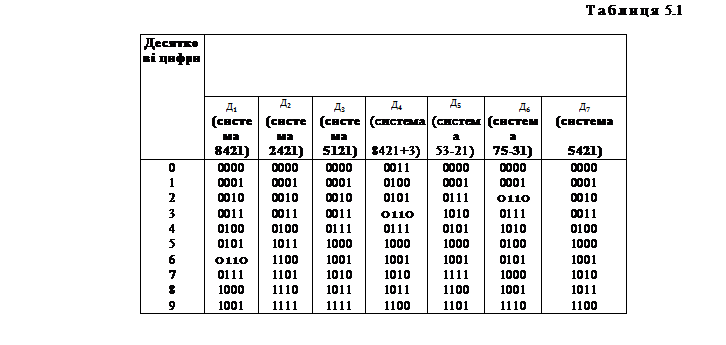
В таблиці для кожного Д-кода вказані дозволені комбінації. Всі інші комбінації – заборонені.
Наявність дозволених і заборонених комбінацій – дуже важлива властивість Д-кодів. Воно відрізняє їх від звичайних позиційних систем числення, в яких всі комбінації – дозволені. Розглянемо найбільш поширені Д-коди. Код  прямого заміщення (система 8421). В коді
прямого заміщення (система 8421). В коді  дозволені комбінації, які відповідають двійковим еквівалентам десяткових цифр з вагою розрядів, рівних степеням підстави 2. Для цього коду не виконується умова (5.2),так як цифри є доповненням до 9, не виходять простими інвертируванням наборів тетрад.
дозволені комбінації, які відповідають двійковим еквівалентам десяткових цифр з вагою розрядів, рівних степеням підстави 2. Для цього коду не виконується умова (5.2),так як цифри є доповненням до 9, не виходять простими інвертируванням наборів тетрад.
Код 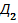 (система 2421). Для кода
(система 2421). Для кода 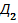 вага розрядів тетради відповідно рівна 2, 4, 2, 1; таблиця кодування ділиться на 2 частини: від 0 до 4
вага розрядів тетради відповідно рівна 2, 4, 2, 1; таблиця кодування ділиться на 2 частини: від 0 до 4 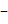 тетради повторюють двійкові еквіваленти, від 5 до 9 – в порівнянні з двійковою системою кожна тетрада містить надлишок +0110. Це дає можливість любу цифру однієї частини таблиці перетворити в її доповнення до 9 простим інтегруванням.
тетради повторюють двійкові еквіваленти, від 5 до 9 – в порівнянні з двійковою системою кожна тетрада містить надлишок +0110. Це дає можливість любу цифру однієї частини таблиці перетворити в її доповнення до 9 простим інтегруванням.
Код  (система 8421+ 3). Для цього кода всі тетради мають значення на три одиниці більше, чим тетради кода
(система 8421+ 3). Для цього кода всі тетради мають значення на три одиниці більше, чим тетради кода 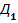 (звідци назва кода), і для нього не існує цілочисельних значень ваги, котрі задовільняли би (5.3)
(звідци назва кода), і для нього не існує цілочисельних значень ваги, котрі задовільняли би (5.3)
Коди  (система 53 – 21) і
(система 53 – 21) і  ( система 75 – 31). Ці коди відрізняються від вищезгаданих кодів тим, що для них деяка вага має негативнее значення.
( система 75 – 31). Ці коди відрізняються від вищезгаданих кодів тим, що для них деяка вага має негативнее значення.
В обчислюваних машинах різного призначення частіше всього використовуються коди 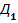 і
і  .
.
5.2 Формальні правила порозрядного складання в Д-кодах
Для визначення формальних правил порозрядного складання чисел, представлених в Д-коді, розглянемо ті особливості котрі притаманні цим кодам.
1. Наявність дозволених і заборонених комбінацій. Появлення забороненої комбінації при появленні помилки або ж при необхідності ввести коректування результата.
2. При складанні тетрад виникає потетрадний перенос  = 16 замість порозрядного переносу
= 16 замість порозрядного переносу  = 10. Це призводить до необхідності корекції результата.
= 10. Це призводить до необхідності корекції результата.
На справді якщо складаються числа  …
…  і
і 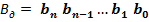 , то сума
, то сума 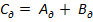 і
і

де  – і-й розряд суми;
– і-й розряд суми; 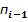 – перенос із молодшої тетради;
– перенос із молодшої тетради; 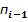 = {0,1},
= {0,1}, 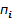 = [0,1], q = 10. Далі виведем правила складання стосовно до Д-кодів. При складанні чисел в коді
= [0,1], q = 10. Далі виведем правила складання стосовно до Д-кодів. При складанні чисел в коді 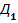 можуть виникнути наступні ситуації.
можуть виникнути наступні ситуації.
1.Нехай 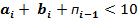 , де
, де 
 - тетради кода
- тетради кода 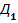 . При складанні в даному розряді числа створюється сума менше 10. Якщо дії над розрядами тетради виробляють за правилами двійкової арифметики, то правильний результат одержують без корекції
. При складанні в даному розряді числа створюється сума менше 10. Якщо дії над розрядами тетради виробляють за правилами двійкової арифметики, то правильний результат одержують без корекції
Приклад 5.1 Скласти тетради  Розв’язок
Розв’язок 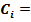
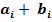 +
+ 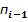 =1001. Відповідь
=1001. Відповідь 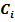 = 1001
= 1001
2.Нехай  , т. е. виникає десяткове перенесення і сума повинна дорівнювати
, т. е. виникає десяткове перенесення і сума повинна дорівнювати  , де
, де  .
.
Свідченням того, що результат неправильний є поява забороненої комбінації, якщо 15 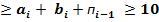 , або поява потетрадного перенесення
, або поява потетрадного перенесення 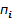 = 16, що перевищує значення десяткового перенесення на 6. Отже потрібна корекція результату в даній тетраді введенням поправки, рівної +0110.
= 16, що перевищує значення десяткового перенесення на 6. Отже потрібна корекція результату в даній тетраді введенням поправки, рівної +0110.
Приклад 5.2 Скласти тетради 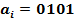 і
і 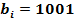 при значенні
при значенні  . Розв’язок
. Розв’язок  +
+ 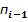 = 1111. Величина
= 1111. Величина  = 1111 - заборонена комбінація. Отже треба ввести поправку:
= 1111 - заборонена комбінація. Отже треба ввести поправку:

т.е результат дорівнює 0101в даній тетраді і утворене перенесення в старшу тетраду
Відповідь  0101,
0101,  .
.
Приклад 5.3 Скласти тетради  ,
, 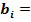 1001 при значенні
1001 при значенні 
Розв’язок  +
+ 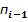 = (1)0001
= (1)0001
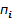
Поява потетрадного перенесення вимагає корекції результату:  = 0001 + 0110 + 0111
= 0001 + 0110 + 0111
Отже:  = 0111,
= 0111,  .
.
Приклади розглянуті вище, дають можливість сформулювати наступні правила потетрадного складання чисел в 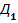 -коді:
-коді:
якщо при потетрадному складанні перенесення в сусідню старшу тетраду не виникає (  ), то результат підсумування не потребує корекції;
), то результат підсумування не потребує корекції;
корекція результату потетрадного складання шляхом добавлення поправки + 0110 потрібна лише, якщо:
а) виникає потетрадне перенесення в старшу тетроду(  1);
1);
б)виникає заборонена комбінація;
Розглянемо приклад підсумування цілих чисел.
Приклад 5.4Скласти числа A= 279 = 0010 0111 1001 і В= 581 = 0101 1000 0001записані в коді 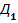 .
.
Розв’язок. Перш за все проводиться потетрадне підсумовування, а потім корекція там, де це необхідно:
A= 0010 0111 1001
+
B= 0101 1000 0001
 + 0111 1111 0101
+ 0111 1111 0101
0110 0110 поправки
 С = 1000←0110 ←0000
С = 1000←0110 ←0000
Тут стрілка вказує передачу одиниці десяткового перенесення. Відповідь: С = 860 = 1000 0110 
При складанні чисел в коді 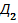 можуть виникнути такі випадки:
можуть виникнути такі випадки:
1. Нехай  <5 і
<5 і 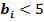 , де
, де  і
і 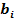 тетради для кода
тетради для кода 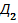 . Тоді: якщо
. Тоді: якщо  +
+ 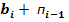 – результат складання корекції не потребує; якщо
– результат складання корекції не потребує; якщо  +
+  ≥ 5 – результат потрапляє в другу частину таблиці кодування, де
≥ 5 – результат потрапляє в другу частину таблиці кодування, де  =
= 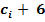 . Тут необхідна корекція результату введенням поправки 0110. Ознака цього поява заборонених комбінацій.
. Тут необхідна корекція результату введенням поправки 0110. Ознака цього поява заборонених комбінацій.
2. Нехай 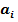 ≥ 5 і
≥ 5 і 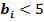 , 15 >
, 15 >  +
+  ≥ 5.
≥ 5.
Так як  =
=  + 6, то при підсумовуванні поправка не потрібна.
+ 6, то при підсумовуванні поправка не потрібна.
3. Нехай 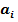 ≥ 5 і
≥ 5 і 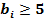 ;
;  1. Тоді: якщо 10 ≤
1. Тоді: якщо 10 ≤  +
+  ≤ 15 - результат вимагає корекції шляхом введення поправки – 0110, тому що з'являється заборонена комбінація *;
≤ 15 - результат вимагає корекції шляхом введення поправки – 0110, тому що з'являється заборонена комбінація *;
якщо ж  +
+  < 15 – результат не потребує корекції.
< 15 – результат не потребує корекції.
При потетрадному підсумовуванні в 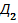 -коді результат підсумовується без корекції вихудить у всіх випадках крім наступних: якщо за відсутності переносу в старшу тетраду
-коді результат підсумовується без корекції вихудить у всіх випадках крім наступних: якщо за відсутності переносу в старшу тетраду  0 ) виникає заборонена комбінація, то потрібно ввести поправку +0110; якщо за наявності переносу в старшу тетраду
0 ) виникає заборонена комбінація, то потрібно ввести поправку +0110; якщо за наявності переносу в старшу тетраду  1) виникає заборонена комбінація то потрібно ввести поправку -0110 (1001 у зворотному коді або 1010 в додатковому коді).
1) виникає заборонена комбінація то потрібно ввести поправку -0110 (1001 у зворотному коді або 1010 в додатковому коді).
Так як поправки бувають позитивні або негативні, то їх введення супроводжується блокуванням ланцюгів міжтетрадного перенесення в період корекції результату.
Приклад 5.5 Скласти числа А = 0010 0100 1110 і В= 0001 1100 1111. Записані в коді 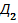 . Розв’язок. Спочатку проводиться потетрадне підсомування, а потім здійснюється корекція:
. Розв’язок. Спочатку проводиться потетрадне підсомування, а потім здійснюється корекція:
А= 0010 0100 1110
+
 В= 0001 1100 1111
В= 0001 1100 1111
С= 0100← 0001← 1101
Результат отриманий без корекції. Відповідь  = +
= + 
Приклад 5.6 Скласти числа А=137 = 0001 = 0011 1101 і В = 457 = 0100 1011 1101 записані в коді 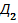 .
.
Рішення. Спочатку проводиться потетрадное підсумовування, а потім корекція:
А= 0001 0011 1101
+ +
 В= 0100 1011 1101
В= 0100 1011 1101
0101 1111 1010
+ +
 0110 0000 1010 поправки
0110 0000 1010 поправки
С= 1011 1111 0100
У молодшій тетраді виникає перенесення 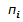 = 1і заборонена комбінація - вводиться поправка 1010 в додатковому коді, в старшій тетраді при
= 1і заборонена комбінація - вводиться поправка 1010 в додатковому коді, в старшій тетраді при  0 виникла заборонена комбінація - поправка вводиться 0110.
0 виникла заборонена комбінація - поправка вводиться 0110.
Відповідь: С= 594 = 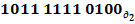
При складанні чисел в коді 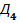 можливі наступні випадки. Нехай
можливі наступні випадки. Нехай 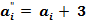 ,
, 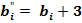 , де
, де  і
і 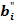 – тетради для кода
– тетради для кода  . Тоді: якщо
. Тоді: якщо 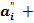
 то
то 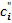 =
=  ;
;  =
=  , результат потребує корекції шляхом поправки – 0011: якщо
, результат потребує корекції шляхом поправки – 0011: якщо 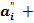

 10, то
10, то 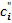 =
=  .
.
Тут виникає десяткове перенесення, яке, за умовою, «забирає» з собою шість надлишкових комбінацій. Отже, в даному випадку потрібна корекція результату шляхом введення поправки +0011.
Приклад 5.7 Скласти числа А=35=0110 1000 і В=28=0101 1011, записані в коді 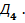 Розв’язок. Спочатку проводиться потетрадне додавання, а потім введення поправок:
Розв’язок. Спочатку проводиться потетрадне додавання, а потім введення поправок:
А= 0110 1000
+
 В= 0101 1011
В= 0101 1011
1100 ←0011
0011 + 0011 поправки
 С= 1001 0110
С= 1001 0110
Відповідь: 
Тут поправки вводяться при блокуванні ланцюгів потетрадного переносу. Правила введення поправок можна сформулювати так: якщо при складанні тетрод не виникає переносу  0 ), то поправка рівна – 0011 (або доповнення + 1101); якщо виникає потетрадний переніс
0 ), то поправка рівна – 0011 (або доповнення + 1101); якщо виникає потетрадний переніс  1 ), то поправка рівна + 0011.
1 ), то поправка рівна + 0011.
Аналогічним образом можна роздивитися правила сумування для інших Д-кодів.
5.3 Представлення від’ємних чисел в Д-кодах
Представлення Д-коду в розрядній сітці машини може здійснюватися у формі з фіксованою або з плаваючою комою. При цьому від’ємні числа повинні представлятися в прямому, оберненому або доповняльному кодах. Тому якщо А = 0,  , де
, де  тетради, то
тетради, то
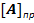 = 1,
= 1, 
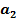 …
… 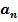 ;
;
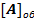 = 1,
= 1, 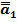
 …
… 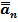 ;
;
 = 1,
= 1, 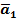
 …
…  ; (5.5)
; (5.5)
де 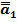 – доповнення до q — 1 у всіх тетрадах;
– доповнення до q — 1 у всіх тетрадах; 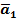 - доповнення до q — 1 у всіх тетрадах, за винятком молодшої, для якої це доповнення до q = 10.
- доповнення до q — 1 у всіх тетрадах, за винятком молодшої, для якої це доповнення до q = 10.
З правил перетворення (5.5) випливає, що
 +
+  = q – 1 (5.6)
= q – 1 (5.6)
Це означає, що для Д-кодів, для яких виконується умова (5.2), обернений код виходить простим інвертуванням набору тетрад.
Приклад 5.8 Знайти зворотній і додатковий коди в коді 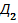 числа для
числа для  . Розв’язок. На підставі (7.5)
. Розв’язок. На підставі (7.5) 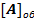 = 1.1110 1101 0010.
= 1.1110 1101 0010.
Використовуючи співвідношення  =
=  , знаходимо доповняльний код:
, знаходимо доповняльний код:  = 1.1110 1101 0011.
= 1.1110 1101 0011.
Додаток одиниці в молодшу тетраду при утворенні доповняльного коду в коді 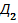 здійснюється за правилами додавання коду для цього. Відповідь:
здійснюється за правилами додавання коду для цього. Відповідь: 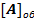 =1,111011010010
=1,111011010010 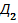 ,
,  = 1,1110 1101 0011
= 1,1110 1101 0011 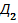 .
.
Приклад 5.9. Знайти обернений і доповняльний коди в коді Д4 для числа А=-0,4591=0,0111100011000100
Розв’язок. На підставі (5.5)
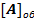 =1,1000 0111 0011 1011 ;
=1,1000 0111 0011 1011 ;
 = 1,1000 0111 0011 1100;
= 1,1000 0111 0011 1100;
Код Д1 відрізняється тим, що для нього не виконується умова (5.2). Ця особливість коду впливає на перетворення зворотнього або додаткового коду, так як інвертування набору тетрад означає отримання доповнення до 24 -1= 15. Отже, необхідно прибрати різницю. Один з використовуваних при цьому прийомів полягає в тому, що в усі цифрові тетради числа в коді Д1 добавляєтся +0110 і після цього проводиться інвертування набору. Отримане зображення являє собою обернений код числа.
Приклад 5.10. Отримати обернений код в коді Д1 для числа А=-0,256=
-0,0010 0101 0110 Д1
Розв’язок. Спочатку до всіх тетрад додається 0110:
0,0010 0101 0110
+ + +
 0110 0110 0110
0110 0110 0110
0,1000 1011 1100
Після інвертування цього набору отримуємо 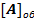 =1,0111 0100 0011 Д1 . Відповідь:
=1,0111 0100 0011 Д1 . Відповідь: 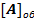 =1,0111 0100 0011 Д1.
=1,0111 0100 0011 Д1.
5.4 Виконання операцій додавання і віднімання чисел в Д-кодах
Всі арифметичні дії в Д-кодах виконуються над операндами за формальними правилами десяткової арифметики, сформульованим вище.
Виникаючі при цьому специфічні особливості доцільно розглянути на конкретних прикладах.
Приклад 5.11. Скласти в коді Д1 на суматорі доповняльного коду числа
А= - 0.1000 00010 0101 і В= 0.1001 0100 0110.
Розв’язок. Вихідні числа представляються в доповняльному коді і їх зображення складаються: 
 = 1. 0001 0111 0101
= 1. 0001 0111 0101
+

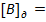 0. 1001 0100 0110
0. 1001 0100 0110
1. 1010 1011 1011
+
0110 0110 0110 поправки

 = 0.← 0001← 0010← 0001
= 0.← 0001← 0010← 0001
Відповідь: С=0,0001 0010 0001Д
Приклад 5.12. Скласти в коді Д1 на суматорі оберненого коду числа А= ̶0.0100 1000 0111 і В= ̶0.0010 0011 0110.
Розв’язок. Вихідні числа представляються у оберненому коді, і їх зображення складаються:
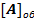 = 1. 0101 0001 0010
= 1. 0101 0001 0010
+
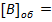 1. 0111 0110 0011
1. 0111 0110 0011
 + 0. 1100 0111 0110
+ 0. 1100 0111 0110
0110 0000 0000 поправки

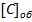 = 1.←0010 ← 0111 ← 0110
= 1.←0010 ← 0111 ← 0110
При корекції в коді Д1, ланцюги міжтетрадного перенесення в суматорах не блокуються. Відповідь отримуємо після перетворення результату з оберненого коду.
Відповідь: С=-0,0111 0010 0011Д.
Приклад 5.13. Скласти в коді Д2 на суматорі доповняльного коду числа А= ̶0.0000 1101 0011 1011 і В= ̶0.0000 1111 0010 1011.
Розв’язок. Якщо все робити за правилами, то [A]Д =1, 1111 0010 1100 0101. В останній тетраді отримана заборонена комбінація, що свідчить про необхідність корекції шляхом введення поправки 0110:
 0101
0101

Аналогічно для другого числа отримуємо в останній тетраді 1011. Отже,

 [А ]Д= 1. 1111 0010 1100 1011
[А ]Д= 1. 1111 0010 1100 1011
 [В]Д= 1. 1111 0000 1101 1011
[В]Д= 1. 1111 0000 1101 1011
1. ← 1110 ← 0011←1010 ← 0110
 0000 0000 1010 1010 поправки
0000 0000 1010 1010 поправки
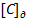 = 1. 1110 0011 0100 0000
= 1. 1110 0011 0100 0000
Відповідь: С=-0,0001 1100 1100 0000Д2.
Приклад 5.14. Скласти на суматорі оберненого коду (система Д2 ) числа А=0,1110 1011 0011Д2 і В=-0,1100 0100 1011Д2.
Розв’язок. Спочатку числа записуються в оберненому коді і їх зображення складаються:


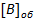 = 1. 0011 1011 0100
= 1. 0011 1011 0100

 = 0. 1110 1011 0011
= 0. 1110 1011 0011

 0. ← 0010 ← 0110← 1000
0. ← 0010 ← 0110← 1000
 0000 1010 0110 поправки
0000 1010 0110 поправки
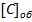 = 0. 0010 0000 1110
= 0. 0010 0000 1110
Відповідь: 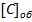 =0,0010 0000 1110Д2
=0,0010 0000 1110Д2
Пример 5.15. Скласти в коді Д4 на суматорі оберненого коду числа А= ̶0.1011 1100 0111 1001 і В=0.0011 1000 1001 1010.
Розв’язок. Спочатку числа записуються у оберненому коді і потім складаються зображення:


 = 1. 0100 0011 1000 0110
= 1. 0100 0011 1000 0110
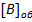 = 0. 0011 1000 1001 1010
= 0. 0011 1000 1001 1010

 1. 0111 1100 ←0010 ← 0000
1. 0111 1100 ←0010 ← 0000

 1101 1101 0011 0011 поправки
1101 1101 0011 0011 поправки
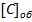 = 1. 0100 1001 0100 0011
= 1. 0100 1001 0100 0011
Розглянуті вище приклади виконання операцій додавання в Д-кодах дозволяють зробити ряд загальних зауважень; корекція результату може здійснюватися автоматично або програмним шляхом, або за допомогою апаратних засобів. Перший метод потребує розробки спеціального блоку управління, а другий - ускладнення схеми власне суматора. Це завдання розробник вирішує в конкретній постановці в залежності від вимог. На практиці частіше використовується схемний метод корекції.
По викладеним вище правилам реалізуються алгоритми складання (віднімання) чисел, представлених у формі з фіксованою комою на спеціальних десяткових суматорах.
Для десяткових чисел з плаваючою комою використовують ту саму методику, що і для двійкових чисел: порядки чисел перед складанням вирівнюються (меншому числу присвоюється порядок більшого числа) і по закінченні операції виробляється нормалізація результату. При цьому з боку молодших розрядів відводиться додаткова тетрада, використовувана при зрушеннях вправо.
Читайте також:
- Активні операції банків
- Активні операції банків з цінними паперами
- Активні операції комерційних банків
- Активні операції центральних банків.
- Алгебраїчні операції
- Аналітико-конструктивні операції
- Арифметичні дії над дійсними невід’ємними числами. Їхні властивості
- Арифметичні й логічні вирази в Excel
- Арифметичні оператори
- Арифметичні операції
- Арифметичні операції в різних системах числення
- Арифметичні операції над цілими числами
| <== попередня сторінка | | | наступна сторінка ==> |
| Множення чисел на двійковому суматорі оберненого коду | | | Тема 7. Елементарні функції алгебри логіки. Функціонально-повні системи логічних функцій |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |