
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Тема 7. Елементарні функції алгебри логіки. Функціонально-повні системи логічних функцій
7.1 Елементарні функції алгебри логіки.
7.2 Функціональна повнота системи функцій алгебри логіки і наборів логічних елементів.
7.1 Елементарні функції алгебри логіки.
Математичний апарат, який описує дії дискретних пристроїв, базується на алгебрі логіки, її ще називають по імені автора – англійського математика Джорджа Буля (1815 – 1864) булевою алгеброю. Практичне застосування алгебри логіки першим з найшов американський вчений Клод Шеннону 1938 р. при дослідженні електричних кіл з контактними вимикачами.
Для формального опису цифрових автоматів використовується апарат алгебри логіки. Логічною (булевою) змінною називається величина, яка може приймати тільки два значення 0і 1. Сукупність різних значень змінних називаються набором.
Основним предметом булевої алгебри є висловлювання – просте твердження, про яке можна стверджувати: істинне воно (позначають символом 1) або хибне (позначають символом 0). Прості висловлювання позначають буквами, наприклад X1, X 2, K Xm , які у цифровій техніці називають змінними (аргументами).
Уданий час головна задача алгебри логіки – аналіз, синтезі структурне моделювання будь-яких дискретних скінчених систем.
Змінну із скінченим числом значень (станів) називають перемикальною, а з двома значеннями – булевою.
Операція – це чітко визначена дія над одним або декількома операндами, яка створює новий об’єкт (результат).
У булевій операції операнди і результат набувають “ булевого значення 1” і “ булевого значення 0”.
Булеві функції можуть залежати від однієї, двох і в цілому n -змінних.
Булева функція n – аргументів може мати до N = 2n наборів. Оскільки функції приймають тільки два значення, загальне число булевих функцій n –
аргументів дорівнює 2n = 22n . Отже, функція одного аргумента може мати чотири значення: y = x; y = x; y =1 (константа 1); y =0 (константа 0).
Два аргументи надають 16 значень функції. Логічні функції двох змінних приведені в таблиці 7.1.
Основними булевими операціями є заперечення (операція НЕ, інверсія), диз’юнкція (операція АБО, логічне додавання, об’єднання) і кон’юнкція (операція І, логічне множення).
Таблиця 7.1
| Аргументи | Функція | Назва логічної функції | ||||
| X1 0 | ||||||
| X2 0 | ||||||
| F0=0 | Константа 0 | |||||
| F1=x1 ∧ x2 | Кон’юнкція, (операція І ) | |||||
F2=x1∧ 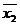
| Заперечення по x2 | |||||
| F3 =x1 | Повторення (тавтологія) x1 | |||||
F4= 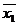 ∧ x2 ∧ x2
| Заперечення по x1 | |||||
| F5 =x2 | Повторення (тавтологія) x2 | |||||
| F6 =x1⊕x2 | Виключаюче АБО (додавання по модулю 2) | |||||
| F7=x1 ∨x2 | Диз’юнкція (операція АБО); | |||||
| F8 =x1↓x2 | Стрілка Пірса (операція АБО-НЕ) | |||||
| F9=x1~ x2 | Еквівалентність | |||||
F10 = 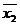
| Заперечення (інверсія) x2 | |||||
F11=x2→x1= 
| Імплікація від x2 до x1 | |||||
F12= 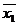
| Заперечення (інверсія x1 ) | |||||
F13=x1 →x2= 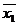 ∨ x2 ∨ x2
| Імплікація від x1 до x2 | |||||
F14=x1|x2= 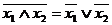
| Штрих Шеффера (операція І-НЕ) | |||||
| F15 = 1 | Константа 1 | |||||
Операції заперечення, диз’юнкції і кон’юнкції можна задати за допомогою таблиць істинності, у яких зліва подані значення операндів, а справа значення булевої функції.
7.2 Функціональна повнота системи функцій алгебри логіки і наборів логічних
елементів
Основна вимога, яка ставиться до набору логічних елементів, полягає в тому, щоб за допомогою цього набору можна було побудувати будь-яку логічну схему. З огляду на те, що функціонування елементів однозначно описується функціями алгебри логіки (ФАЛ), застосовуючи операцію суперпозиції, можна з деякої системи ФАЛ отримати будь-яку, скільки завгодно складну ФАЛ. Тоді ця деяка система ФАЛ буде називатися функціонально повною (ФПС ФАЛ).
Функціонально повним є такий набір ФАЛ, який містить хоча б одну функцію, яка:
не зберігає константу "0";
не зберігає константу "1";
не є монотонною;
не є самодвоїстою;
не є лінійною.
Якщо функція f на нульовому наборі змінних дорівнює 0, тобто f(0,0,...,0)=0, то ця
функція зберігає константу "0".
Якщо функція f на одиничному наборі змінних дорівнює 1, тобто f(1,1,...,1)=1, то ця
функція зберігає константу "1".
ФАЛ називається монотонною, якщо при будь-якому зростанні кількості "1" у
послідовності сусідніх (тобто таких, які відрізняються тільки в одному розряді) наборів
змінних (х0,х1,...,xn) значення функції не зменшується.
ФАЛ називається самодвоїстою, якщо на кожній парі протилежних наборів (x0,x1,...,xn) та (/x0,/x1,...,/xn) вона приймає протилежні значення, тобто, якщо виконується умова
f(x0,x1,...,xn) = /f(/x0,/x1,...,/xn),
де знаком "/" позначена операція інверсії.
ФАЛ називається лінійною, якщо її можна зобразити поліномом Жегалкіна без
добутків змінних
f(x0,x1,...,xn) = a0·x0 # a1·x1 # ... # an·xn,
де ai = (0, 1);
· - позначення операції І;
# - позначення операції "додавання за модулем 2".
Для того щоб записати функцію, яка задана таблично, у вигляді полінома Жегалкіна, досить записати цю функцію у вигляді суми за модулем 2 тих наборів аргументів, на яких функція дорівнює 1. Після цього потрібно всі змінні, які входять до отриманого виразу з інверсіями, замінити за допомогою співвідношення /х = х # 1, розкрити дужки і звести подібні члени за допомогою тотожності
х # х # ... # х = х, якщо кількість х непарна;
х # х # ... # х = 0, якщо кількість х парна.
У табл. 7.2 наведені функції двох змінних і позначкою * вказана їх належність
кожному з класів ФАЛ. У графі "Клас" позначено:
0 - зберігає константу "0";
1 - зберігає константу "1";
Л - лінійна;
М - монотонна;
С - самодвоїста.
Таблиця 7.2
| х0 | Назва ФАЛ | Вираз ФАЛ | Клас | ||||||||
| х1 | Л | М | С | ||||||||
| f0 | константа "0" | * | * | * | |||||||
| f1 | кон'юнкція, І | х0·х1 | * | * | * | ||||||
| f2 | заборона по х1 | х0·/х1 | * | ||||||||
| f3 | х0 | х0 | * | * | * | * | * | ||||
| f4 | заборона по х0 | /х0·х1 | * | ||||||||
| f5 | х1 | х1 | * | * | * | * | * | ||||
| f6 | сума за mod 2 | 0 х0·/х1 v /х0·х1 | * | * | |||||||
| f7 | диз'юнкція, АБО | х0 v х1 | * | * | * | ||||||
| f8 | АБО-НЕ (Пірса) | /(х0 v х1) | |||||||||
| f9 | рівнозначність | х0·х1 v /х0·/х1 | * | * | |||||||
| f10 | інверсія х1 | /х1 | * | * | |||||||
| f11 | імплікація звор. | х0 v /х1 | * | ||||||||
| f12 | інверсія х0 | /х0 | * | * | |||||||
| f13 | імплікація пряма | /х0 v х1 | * | ||||||||
| f14 | І-НЕ (Шефера) | /(х0·х1) | |||||||||
| f15 | константа "1" | * | * | * |
Таблиця 7.3
Таблиця 7.4
| a | b | c | f |
| a b c | f | a b c | f | a b c | f | a b c | f | a b c | f | a b c | f |
| 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | 0 0 0 | ||||||
| 0 0 1 | 0 0 1 | 0 1 0 | 0 1 0 | 1 0 0 | 1 0 0 | ||||||
| 0 1 1 | 1 0 1 | 0 1 1 | 1 1 0 | 1 0 1 | 1 1 0 | ||||||
| 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | 1 1 1 | ||||||
| а | б | в | г | д | е |
Таблиця 7.5
| abc | f | abc | f |
Приклад 7.1. Перевірити, чи створює функція трьох змінних, яка задана табл. 7.3,функціонально повну систему.
1) Оскільки на нульовому наборі f(0,0,0) = 1, то ця функція не зберігає константу "0".
2) Оскільки на одиничному наборі f(1,1,1) = 0, то ця функція не зберігає константу "1".
3) Послідовності сусідніх наборів подані в табл. 7.4 а, ..., е.
Оскільки на всіх шести послідовностях сусідніх наборів функція не є монотонною (а досить було б і на одному), то функція не є монотонною взагалі.
4) Пари протилежних наборів наведені в табл. 7.5.
Оскільки на кожній парі протилежних наборів функція приймає протилежні значення, то функція є самодвоїстою.
5) Для визначення лінійності функції подамо її у вигляді полінома Жегалкіна
f=/a/b/c#/ab/c#/abc #ab/c=(1#a)(1#b)(1#c) # (1#a)b(1#c) # (1#a)bc # ab(1#c) =
=(1#a)(1#b#c#bc) # b(1#a#c#ac) # (bc # abc) # (ab # abc) =
=(1#b#c#bc#a#ab#ac#abc)#(b#ab#bc#abc)#(bc#abc)#(ab#abc) =
= 1 # ( = 1)
# a # ( = a)
# b # b # ( = 0)
# c # ( = c)
# ab # ab # ab # ( = ab)
# ac # ( = ac)
# bc # bc # bc # ( = bc)
# abc # abc # abc # abc = ( = 0)
= 1 # a # c # ab # ac # bc.
Оскільки поліном містить добутки змінних, то функція не є лінійною. Отже, із п'яти необхідних для створення ФПС властивостей відсутня одна - несамодвоїстість, тому дана функція не утворює ФПС.
Читайте також:
- I. Органи і системи, що забезпечують функцію виділення
- I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
- II. Анатомічний склад лімфатичної системи
- IV. Розподіл нервової системи
- IV. Система зв’язків всередині центральної нервової системи
- IV. Філогенез кровоносної системи
- POS-системи
- T. Сутність, етіологія та патогенез порушень опорно-рухової системи
- V. Етичні правила психологічних досліджень
- VI. Філогенез нервової системи
- XV. Фінансові результати від первісного визнання та реалізації сільськогосподарської продукції та додаткових біологічних активів
- А) Заробітна плата її форми та системи.
| <== попередня сторінка | | | наступна сторінка ==> |
| Тема 5. Арифметичні операції в двійково-десяткових СЧ | | | Тема 8. Форми представлення функцій алгебри логіки |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |