
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ТЕМА 4. Моделі парної лінійної та нелінійної регресії
План
1. Модель парної лінійної регресії (загальний вигляд та класичні припущення, приклади).
2. Знаходження параметрів ПЛР методом МНК.
3. Економічні показники аналізу ПЛР.
4. Перевірка моделі ПЛР на адекватність статистичним даним.
5. Побудова довірчих інтервалів параметрів моделі ПЛР і теоретичних значень показника.
6. Знаходження прогнозного значення показника та його довірчого інтервалу. 7. Коефіцієнт еластичності.
8. Модель парної нелінійної регресії (види і приклади).
9. Методологія дослідження моделей ПНЛР.
9.1. Перевірка моделі ПНЛР на адекватність статистичним даним.
9.2. Побудова довірчих інтервалів параметрів моделі ПНЛР і теоретичних значень показника.
9.3. Прогноз показника та його довірчий інтервал.
9.4. Коефіцієнт еластичності.
10. Приклади застосування моделей ПНЛР у бізнесі та фінансах.
1. Модель парної лінійної регресії (загальний вигляд і класичні припущення, приклади). Зв'язок між різними явищами в економіці складний і різноманітний. На рівень розвитку одного показника можуть впливати багато факторів, причому рівень їхнього впливу різний. Ці закономірності потрібно враховувати під час планування, прогнозування та проведення економічного аналізу.
Для вивчення форми зв'язку між показником і факторами на основі статистичних даних використовується регресійний аналіз. Серед парних регресій найбільш поширеною, вивченою і простою в практиці моделювання є парна лінійна регресія.
Парною лінійною регресією  на
на 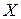 називається одностороння стохастична лінійна залежність між випадковими величинами показника
називається одностороння стохастична лінійна залежність між випадковими величинами показника  і фактора
і фактора 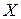 , які знаходяться в причинно-наслідкових відношеннях, причому
, які знаходяться в причинно-наслідкових відношеннях, причому
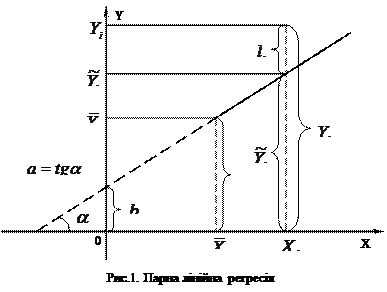 |
зміна фактора викликає зміну показника. Слід відрізняти стохастичну залежність від функціональної. При стохастичній залежності одному значенню фактора може відповідати декілька значень показника, тоді як при функціональній залежності одному значенню аргумента відповідає лише одне значення функції, тобто між аргументом і функцією існує взаємооднозначна відповідність.
Зв'язок між показником  і фактором
і фактором 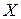 з урахуванням можливих відхилень запишемо у вигляді:
з урахуванням можливих відхилень запишемо у вигляді:
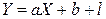 (1),
(1),
де 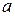 і
і 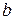 – невідомі параметри регресії,
– невідомі параметри регресії, 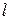 – випадкова змінна, що характеризує відхилення паралельно осі ОХ спостережуваних точок від лінії регресії.
– випадкова змінна, що характеризує відхилення паралельно осі ОХ спостережуваних точок від лінії регресії.
Таким чином, показник  зображується у вигляді систематичної складової
зображується у вигляді систематичної складової 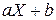 і випадкової величини
і випадкової величини 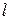 . Залежність
. Залежність
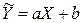 (2),
(2),
яка характеризує середнє значення показника  , для цього значення фактора
, для цього значення фактора 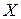 , називається регресією. Можемо сказати інакше, регресія характеризує тенденцію зміни показника, зумовлену впливом зміни фактора. Залежність
, називається регресією. Можемо сказати інакше, регресія характеризує тенденцію зміни показника, зумовлену впливом зміни фактора. Залежність 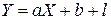 характеризує індивідуальне значення показника
характеризує індивідуальне значення показника  з урахуванням можливих відхилень від середніх значень.
з урахуванням можливих відхилень від середніх значень.
Справжні значення параметрів обчислити не можна, оскільки ми маємо обмежене число спостережень, тому здобуті розрахункові значення параметрів 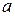 і
і 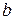 є статистичними оцінками справжніх параметрів
є статистичними оцінками справжніх параметрів 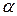 і
і 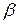 . Позначимо оцінки параметрів через
. Позначимо оцінки параметрів через 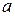 і
і 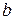 . Тоді рівняння парної регресії
. Тоді рівняння парної регресії 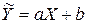 (рис.1) буде оцінкою моделі
(рис.1) буде оцінкою моделі 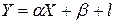 .
.
Розглянемо різницю 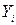 та
та 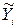 , (
, ( 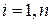 ), записану у такому вигляді:
), записану у такому вигляді:
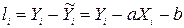 (3),
(3),
де 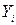 – фактичні, а
– фактичні, а 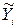 – розрахункові значення показника,
– розрахункові значення показника,
 – відхилення спостережуваної точки (
– відхилення спостережуваної точки ( 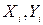 ) від точки (
) від точки ( 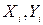 ).
).
На відхилення  накладаються такі припущення:
накладаються такі припущення:
1)  -випадкові величини;
-випадкові величини;
2) математичне сподівання  дорівнює нулю, тобто, М [
дорівнює нулю, тобто, М [  ]=0 та дисперсія
]=0 та дисперсія  стала величина, тобто,
стала величина, тобто, 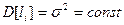 ,
, 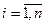 ;
;
3) випадкові величини  та
та 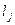 некорельовані між собою, якщо
некорельовані між собою, якщо 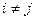 , тобто кореляційний момент (або коефіцієнт коваріації)
, тобто кореляційний момент (або коефіцієнт коваріації)  та
та 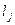 дорівнює нулю, якщо
дорівнює нулю, якщо 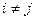 , К [
, К [  ,
, 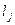 ] =0;
] =0;
4) випадкові величини  розподілені за нормальним законом розподілу.
розподілені за нормальним законом розподілу.
2. Знаходження параметрів ПЛР методом МНК. Для знаходження параметрів парної лінійної регресії використовують метод найменших квадратів, суть якого полягає в тому, що сума квадратів відхилень розрахункових значень показника від фактичних повинна прямувати до мінімума.
Запишемо функціонал методу:
Q ( 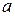 ,
, 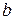 ) =
) = 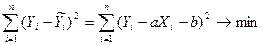 (4),
(4),
З необхідної умови існування мінімума функціонала (4) запишемо систему нормальних рівнянь у вигляді:
 (5).
(5).
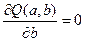
Спростивши вигляд системи (5), отримаємо формули для знаходження числових значень параметрів ПЛР. Параметр 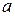 рівняння парної лінійної регресії
рівняння парної лінійної регресії 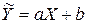 визначається за формулою:
визначається за формулою:
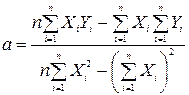 (6).
(6).
Параметр 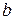 рівняння парної лінійної регресії
рівняння парної лінійної регресії 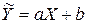 визначається за формулою:
визначається за формулою:
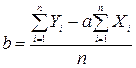 (7).
(7).
Використовуючи дослідні значення фактора і показника за формулами (6) і (7), знайдемо числові значення параметрів рівняння парної лінійної регресії.
У формулі (7) поділимо почленно вирази й отримаємо спрощену формулу для визначення параметра 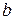 рівняння парної лінійної регресії:
рівняння парної лінійної регресії:
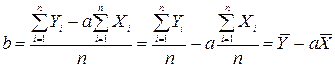 (8).
(8).
Звідси випливає, що лінія регресії проходить через точку, координати якої є середні значення показника  і фактора
і фактора 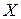 .
.
3. Економічні показники аналізу ПЛР.Для визначення тісноти та напрямку зв'язку між величинами 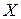 і
і  вводиться коефіцієнт кореляції, який визначається за формулою:
вводиться коефіцієнт кореляції, який визначається за формулою:
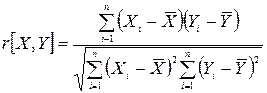 (9).
(9).
| |
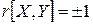 , то зв'язок між величинами функціональний., якщо
, то зв'язок між величинами функціональний., якщо 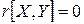 , то зв'язок відсутній.
, то зв'язок відсутній.
Опишемо залежність тісноти зв'язку між явищами від величини коефіцієнта кореляції 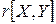 .
.
Якщо 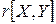 знаходиться в межах (-1; -0,7] та [0,7; 1), то зв'язок сильний, тобто зміна фактора призводить до сильної зміни показника.
знаходиться в межах (-1; -0,7] та [0,7; 1), то зв'язок сильний, тобто зміна фактора призводить до сильної зміни показника.
Якщо 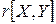 знаходиться в межах (-0,7; -0,5] та [0,5; 0,7), то зв'язок середній, тобто зміна фактора не сильно впливає на зміну показника.
знаходиться в межах (-0,7; -0,5] та [0,5; 0,7), то зв'язок середній, тобто зміна фактора не сильно впливає на зміну показника.
Якщо 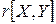 знаходиться в межах (-0,5; 0) та (0; 0,5), то зв'язок слабкий.
знаходиться в межах (-0,5; 0) та (0; 0,5), то зв'язок слабкий.
Якщо 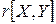 <0, то зв'язок між величинами обернений, тобто зі збільшенням значення фактора зменшується значення показника.
<0, то зв'язок між величинами обернений, тобто зі збільшенням значення фактора зменшується значення показника.
Якщо ж 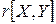 >0, то зв'язок між величинами прямий, тобто зі збільшенням значення фактора збільшується значення показника.
>0, то зв'язок між величинами прямий, тобто зі збільшенням значення фактора збільшується значення показника.
Вибірковий коефіцієнт кореляції, здобутий за вибірковими даними, є точковою оцінкою коефіцієнту кореляції і, в свою чергу, є випадковою величиною. Тому доцільно зробити перевірку гіпотези про відсутність кореляційного зв'язку. Для цього перевіряється нульова гіпотеза Н0: 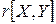 =0 і альтернативна гіпотеза Н1:
=0 і альтернативна гіпотеза Н1: 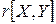 ¹0.
¹0.
Припускаємо, що двомірна випадкова величина розподілена за нормальним законом. Для вибірки обчислюється статистика Стьюдента:
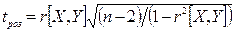 , (10),
, (10),
яка має розподіл Стьюдента з 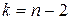 ступенями вільності. Для заданої ймовірності
ступенями вільності. Для заданої ймовірності 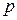 і
і 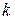 ступенів вільності знаходять табличне значення
ступенів вільності знаходять табличне значення 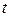 – статистики.
– статистики.
Якщо 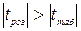 , то із заданою надійністю
, то із заданою надійністю 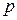 гіпотезу про відсутність кореляційного зв'язку між випадковими величинами
гіпотезу про відсутність кореляційного зв'язку між випадковими величинами 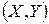 слід відкинути і прийняти альтернативну їй гіпотезу, про наявність кореляційної залежності між цими випадковими величинами з коефіцієнтом кореляції відмінним від нуля.
слід відкинути і прийняти альтернативну їй гіпотезу, про наявність кореляційної залежності між цими випадковими величинами з коефіцієнтом кореляції відмінним від нуля.
Для аналізу якості існуючої залежності між двома величинами за допомогою парної лінійної регресії часто використовують індекс кореляції, який вводиться через коефіцієнт детермінації. Для парної лінійної регресії коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції.
Коефіцієнт детермінації розраховується за формулою:
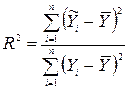 (11).
(11).
Для парної лінійної регресії коефіцієнт детермінації дорівнює квадрату коефіцієнта кореляції:
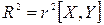 (12).
(12).
Коефіцієнт детермінації показує ступінь варіації показника  під впливом фактора
під впливом фактора 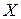 . Значення коефіцієнта детермінації знаходиться в межах від 0 до 1.
. Значення коефіцієнта детермінації знаходиться в межах від 0 до 1.
Якщо 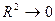 , то варіація фактора мало впливає на варіацію показника. Якщо
, то варіація фактора мало впливає на варіацію показника. Якщо 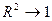 , то варіація показника сильно обумовлена варіацією фактора.
, то варіація показника сильно обумовлена варіацією фактора.
| |
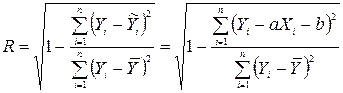 (13).
(13).
Індекс кореляції змінюється в межах від 0 до 1. Чим ближче спостережуване значення наближається до лінії регресії, тим ближче значення 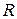 наближається до 1.
наближається до 1.
Надійні межі індексу кореляції визначаються через оцінку середньоквадратичного відхилення 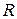 ,
, 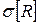 за формулами:
за формулами:
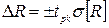 ,
, 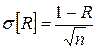 (14).
(14).
Тоді надійний інтервал індексу кореляції буде мати вигляд:
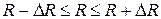 .
.
4. Перевірка моделі ПЛР на адекватність статистичним даним.Для визначення адекватності прийнятої економетричної моделі експериментальним даним скористаємося 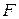 -критерієм Фішера, який полягає в наступному:
-критерієм Фішера, який полягає в наступному:
Розраховуємо значення критерію за формулою:
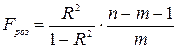 (15).
(15).
Знаходимо табличне значення 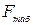 за заданою ймовірністю
за заданою ймовірністю 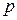 та числом ступенів вільності
та числом ступенів вільності 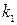 і
і  які визначаються за формулами:
які визначаються за формулами:
 ,
, 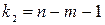 (16),
(16),
де 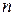 – кількість проведених спостережень;
– кількість проведених спостережень;
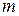 – кількість факторів, які мають суттєвий вплив на показник.
– кількість факторів, які мають суттєвий вплив на показник.
Якщо розрахункове значення критерію Фішера більше за табличне, тобто:
 ,
,
то прийнята економетрична модель вважається адекватною експериментальним даним і для неї справедливі всі закономірності функціонування і розвитку, що характерні для реального економічного явища.
У протилежному випадку побудована модель неадекватна експериментальним даним і неможе використовуватися для аналізу та прогнозування. У цьому випадку рекомендується збільшити кількість спостережень.
| |
Читайте також:
- CMM. Визначення моделі зрілості.
- ISO 15504.Структура еталонної моделі
- Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
| <== попередня сторінка | | | наступна сторінка ==> |
| ТЕМА 3. Допоміжний математичний матеріал | | | Побудова довірчих інтервалів параметрів моделі ПЛР і теоретичних значень показника. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |