Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ТЕМА 3. Допоміжний математичний матеріал

План

Матриці: поняття, види, операції, властивості, визначник.
Власні числа матриці.
Диференційне числення в матричній формі.

1. Матриці: поняття, види, операції, властивості, визначник.При розв’язанні економічних задач використовуються таблиці значень, системи регресій, які зручно записувати лаконічно, з використанням матричних позначень.

Матриці – це прямокутні таблиці елементів, розташовані у рядках і стовпцях.

Матриця [А] називається прямокутною матрицею порядку n на m, або nxm (n – число рядків, m – число стовпців).

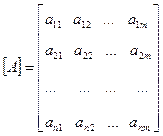
Матриця, в якій число рядків дорівнює числу стовпців, називається квадратною. Порядок квадратної матриці визначається одним числом – кількістю рядків (стовпців).

Матриця, яка складається з одного рядка елементів, називається вектором – рядком.

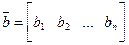
Матриця, яка складається з одного стовпця елементів, називається вектором – стовпцем.

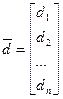
Квадратна матриця називається діагональною, якщо елементи, які не належать головній діагоналі, дорівнюють нулю.

Діагональна матриця, в якій кожен елемент головної діагоналі дорівнює одиниці, називається одиничною і позначається буквою [Е].

Одинична матриця має вигляд:

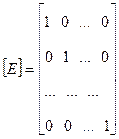
Матриця, в якої всі елементи дорівнюють нулю, називається нульовою.

Квадратна матриця [А] порядку n називається симетричною, якщо виконується умова 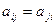для всіх елементів матриці.

Матриця [A] дорівнює матриці [B], якщо вони одинакових розмірів, наприклад, nxm, і мають однакові відповідні елементи:

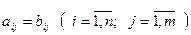Розглянемо дії над матрицями

1. Додавання матриць

Додавання матриць вводиться тільки для матриць одного порядку. Сумою двох матриць [A] і [B] порядку nxm називається матриця [C], яка має такий самий порядок mxn, як і матриці [А] і [В], причому кожен елемент матриці [C] дорівнює сумі відповідних елементів матриць [A] і [B]:

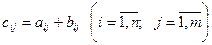
2. Множення числа на матрицю

Добутком числа 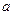на матрицю [A] порядку nxm називається матриця [B] порядку nxm, кожний елемент якої дорівнює добутку числа 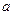на відповідний елемент матриці [A]:

= .

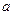
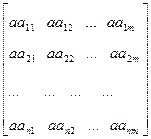Для додавання і множення матриць на число справедливі такі операції:

1) [A] + [B] = [B] + [A] – комутативний закон додавання матриць;

2) [A] + ([B] + [C]) = ([A] + [B]) + [C] – асоціативний закон додавання матриць;

3) 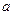(b[A]) = ( 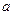b)[A] - асоціативний закон множення чисел на матрицю;

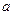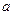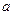4) ([A] + [B]) = [A] + [B] – дистрибутивний закон множення числа на суму матриць;

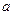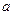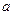5) ( + b)[A] = [A] + [B] - дистрибутивний закон множення cуми чисел на матрицю.

3. Добуток матриць

Добуток двох матриць вводиться лише для узгоджених матриць. Дві матриці [A] і [B] називаються узгодженими, якщо кількість стовпців першої матриці [A] дорівнює кількості рядків другої матриці [B].

Якщо матриці [A] порядку nxm і [B] порядку mxp узгоджені, то добутком цих матриць називається така матриця [С] порядку nxp, для якої елемент 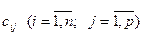дорівнює добутку кожного елемента 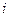-го рядка матриці [A] на 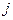-й стовпець матриці [B].

Операція множення матриць не комутативна:

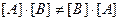Квадратну матрицю можна помножити саму на себе, тобто піднести до квадрата.

Для дій над матрицями справедливі такі властивості:

1) 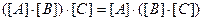- асоціативний закон множення матриць;

2) 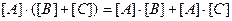- дистрибутивний закон множення матриці на суму матриць;

3) 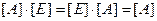- комутативний закон множення квадратної матриці [A] на одиничну матрицю [E] такого ж порядку.

4. Транспонування матриць

Матриця [A] 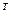називається транспонованою відносно матриці [A], якщо кожен стовпець матриці [A] 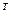є відповідним рядком матриці [A], тобто перший стовпець матриці [A] 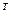є першим рядком матриці [A], відповідно другий стовпець матриці [A] 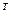є другим рядком матриці [A] тощо.

Для елементів транспонованих матриць виконується умова 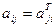. Якщо квадратна матриця [A] симетрична, то виконується умова .

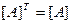Властивості транспонованих матриь:

1. ([A] ) ;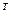

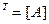2. ([A]+[B]) ;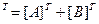

3. ([A] [B])

4. ([A] [B] [C]) .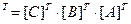

5. Обернена матриця

Ролзглянемо невироджену матрицю п-го порядку.

Квадратна матриця [A] називається невиродженою, якщо її визначник не дорівнює нулю, тобто det [A] 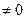, і виродженою або особливою, якщо її визначник дорівнює нулю, тобто det [A] = 0.

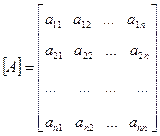Квадратна матриця [A] називається оберненою до квадратної матриці [A] того ж порядку, якщо їх добуток дорівнює одиничній матриці:

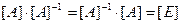6. Визначник матриці

Визначник матриці [A] – це число det [A], яке знаходиться за встановленим правилом.

Для матриці другого порядку визначник обчислюється за формулою:

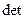[A] = = .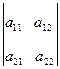

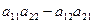Для матриці третього порядку визначник обчислюється за формулою:

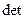[A] = =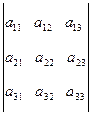

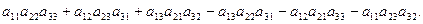
Отже, підсумовуючи сказане, визначник – це функція, яка кожній матриці, за виключенням вироджених, ставить у відповідність дійсне число.

Для обчислення визначників матриць вищих порядків зручно використовувати пакет електронних таблиць Excel.

2. Диференційне числення в матричній формі.Розглянемо деякі випадки диференційного числення в матричній формі, які використовуються в економетрії.

1. Нехай задані вектори

, .

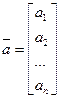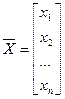Знайдемо частинну похідну за змінною 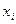від скалярного добутку ( ):

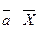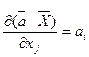звідки випливає, що похідна від скалярного добутку векторів ( 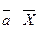) за одним із них дорівнює другому вектору:

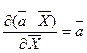2. Розглянемо добуток 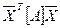, де [A] – квадратна симетрична матриця порядку п:

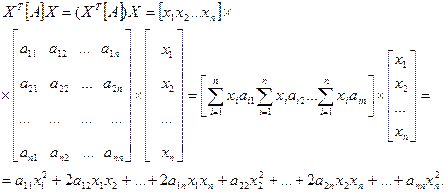Знайдемо частинні похідні за елементами вектора :

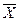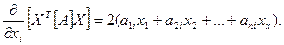
Це подвоєний добуток і-го рядка матриці [A] на вектор стовпець Х:

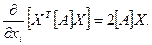
Враховуючи, що 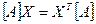, а також, що для симетричної матриці , отримаємо альтернативну формулу:

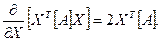
3. Розглянемо квадратичну форму 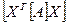як функцію елементів 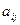матриці [A]. Знайдемо частинну похідну за елементом :

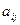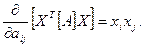
Всього таких похідних буде nxn. Звідси:

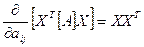4. Знайдемо другу частинну похідну за вектором Х:

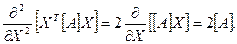Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
	\|	ТЕМА 4. Моделі парної лінійної та нелінійної регресії

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.