
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Побудова довірчих інтервалів параметрів моделі ПЛР і теоретичних значень показника.
Якщо припустити, що розкид спостережень відносно лінійної регресії розподілений за нормальним законом, то надійні межі для параметра 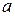 рівняння парної лінійної регресії
рівняння парної лінійної регресії 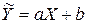 визначається за формулою:
визначається за формулою:
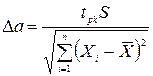 (17),
(17),
де 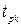 – табличне значення функції Стьюдента, яке визначається за даними значеннями ймовірності
– табличне значення функції Стьюдента, яке визначається за даними значеннями ймовірності 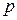 і числом ступенів вільності
і числом ступенів вільності 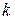 ;
;
 – незсувна і обгрунтована статистична оцінка дисперсії і визначається за формулою:
– незсувна і обгрунтована статистична оцінка дисперсії і визначається за формулою:
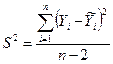 (18).
(18).
Тоді надійний інтервал параметра 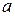 рівняння парної лінійної регресії
рівняння парної лінійної регресії 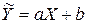 буде мати вигляд:
буде мати вигляд:
 .
.
У тих самих припущеннях надійні межі для параметра 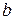 визначають за формулою:
визначають за формулою:
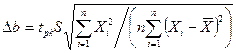 (19).
(19).
| |
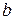 рівняння парної лінійної регресії
рівняння парної лінійної регресії 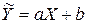 буде мати вигляд:
буде мати вигляд:
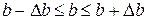 .
.
Надійні межі базисних середніх значень показника  визначаються за формулою:
визначаються за формулою:
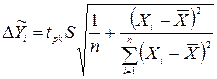 (20).
(20).
Сполучаючи неперервною лінією на графіку всі значення 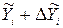 та відповідно
та відповідно 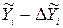 , отримаємо верхню та відповідно нижню межу надійної зони регресії. Частина площини, яка знаходиться між ними, називається надійною зоною парної лінійної регресії.
, отримаємо верхню та відповідно нижню межу надійної зони регресії. Частина площини, яка знаходиться між ними, називається надійною зоною парної лінійної регресії.
Зазначимо, що найкращі припущення із заданою надійністю потрібно очікувати в околі точки 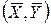 . Надійна зона збільшується при віддаленні
. Надійна зона збільшується при віддаленні 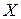 від значення
від значення 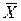 .
.
6. Знаходження прогнозного значення показника та його довірчого інтервалу. Прогнозуванням називається наукове передбачення ймовірнісних шляхів розвитку явищ і процесів для більш-менш віддаленого майбутнього.
Періодом упередження називається проміжок часу від моменту, для якого є останні статистичні дані про досліджуваний об'єкт, до моменту, до якого належить прогноз.
Прогнозування, яке грунтується на збереженні загальної тенденції розвитку явищ у часі, можна звести до добору аналітичних виразів типу 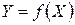 за даними за минуле й екстраполяції здобутих залежностей.
за даними за минуле й екстраполяції здобутих залежностей.
| |
Середнє прогнозне значення показника при значенні фактора відповідно до лінійної регресії визначається за формулою:
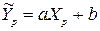 (21).
(21).
Знайдемо надійні межі прогнозу. Запишемо межі надійного інтервалу індивідуального прогнозованого значення
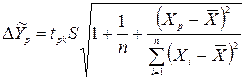 (22).
(22).
Тоді надійний інтервал прогнозу буде мати вигляд:
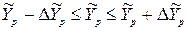 .
.
7. Коефіцієнт еластичності.В економічних задачах для оцінки впливу на показник будь-якого фактора часто використовують коефіцієнт еластичності. В загальній статистиці коефіцієнт еластичності отримують на основі статистичного ряду. Припустимо, що маємо статистичний ряд із базисними даними показника і фактора:

Х Х1 Х2 Х3 ……. Хn
Y Y1 Y2 Y3 ……. Yn
Коефіцієнт еластичності для значення фактора знаходять за формулою:
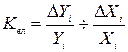 ,
,
де 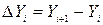 - абсолютне відхилення показника,
- абсолютне відхилення показника,
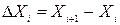 - абсолютне відхилення фактора.
- абсолютне відхилення фактора.
Якщо між фактором і показником знайдена стохастична залежність, то коефіцієнт еластичності для значення фактора 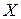 аналогічно можна знайти за формулою:
аналогічно можна знайти за формулою:
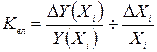 .
.
Якщо зробити граничний перехід при 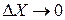 , то отримаємо формулу для точкової оцінки коефіцієнта еластичності:
, то отримаємо формулу для точкової оцінки коефіцієнта еластичності:
 (23).
(23).
Коефіцієнт еластичності показує, на скільки відсотків зміниться показник, якщо фактор зміниться на один відсоток.
Для парної лінійної регресії 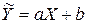 коефіцієнт еластичності знаходиться за формулою:
коефіцієнт еластичності знаходиться за формулою:
 (24).
(24).
За обчисленими значеннями коефіцієнта еластичності будуємо графік залежності коефіцієнта еластичності від числових значень фактора.
8. Модель парної нелінійної регресії (види і приклади). Найбільш поширеною, вивченою і простою в практиці моделювання є парна лінійна регресія. Проте не всі економічні процеси можна нею моделювати. Тому на практиці використовують складніші моделі з нелінійними залежностями між показником y і фактором x, які називаються парними нелінійними регресіями. Для таких регресій зберігається вся методологія досліджень, яку ми детально розглядали у випадку парної лінійної регресії.
Вивчення цієї теми має на меті навчити студента на основі фактичних статистичних даних будувати економічні моделі у формі парної нелінійної регресії і проводити їх повний економічний аналіз. Вивчення даної теми можливе з використанням електронних таблиць Excel.
Парною нелінійною регресією показника Y на фактор X називається нелінійна стохастична залежність між Y і X, які перебувають у причинно-наслідкових відношеннях.
Парна нелінійна регресія буває таких видів:
1) нелінійна за фактором, але лінійна за показником (або квазілінійна);
2) нелінійна і за фактором, і за показником.
Розглянемо приклади парних нелінійних регресій та обчислення їх параметрів:
1) 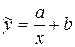 .
.
Заміною 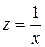 зведемо до виду
зведемо до виду 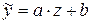 . Параметри будуть обчислюватися за формулами:
. Параметри будуть обчислюватися за формулами:
 ;
;
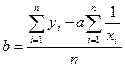 .
.
2) 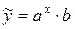 .
.
Прологарифмуємо вираз:
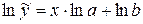 .
.
Заміною 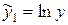 ,
, 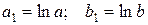 зведемо вираз до лінійного виду
зведемо вираз до лінійного виду 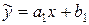 .
.
Параметри регресій будуть обчислюватися за формулами:
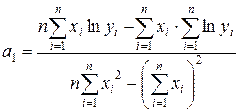 ;
; 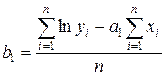 .
.
Остаточно, 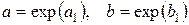 .
.
3) 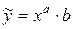
Прологарифмуємо вираз:
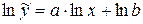 .
.
Заміною 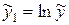 ,
, 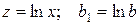 зведемо вираз до лінійного виду
зведемо вираз до лінійного виду 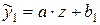 .
.
Параметри регресій будуть обчислюватися за формулами:
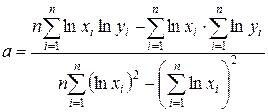
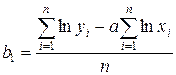 .
.
Остаточно 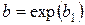 .
.
4) 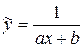 .
.
Заміною 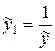 зведемо вираз парної нелінійної регресії до лінійного виду
зведемо вираз парної нелінійної регресії до лінійного виду 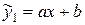 .
.
Параметри будуть обчислюватися за формулами:
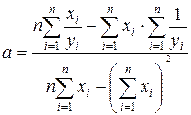 ;
;
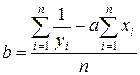 .
.
5) 
Заміною 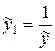 ;
;  зведемо вираз парної нелінійної регресії до лінійного виду
зведемо вираз парної нелінійної регресії до лінійного виду 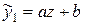 .
.
Параметри будуть обчислюватися за формулами:
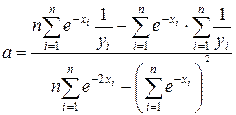 ;
;
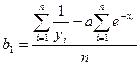 .
.
6)  .
.
Заміною 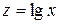 зведемо вираз квазілінійної регресії до лінійного виду
зведемо вираз квазілінійної регресії до лінійного виду 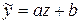 .
.
Параметри будуть обчислюватися за формулами:
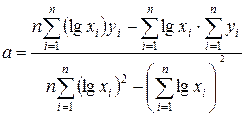 ;
; 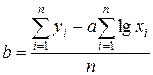 .
.
7) 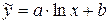
Заміною 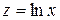 зведемо вираз квазілінійної регресії до лінійного виду
зведемо вираз квазілінійної регресії до лінійного виду 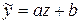 .
.
Параметри будуть обчислюватися за формулами:
 ;
;
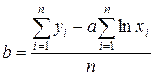 .
.
8) 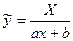 .
.
Заміною 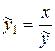 зведемо вираз парної нелінійної регресії до лінійного виду
зведемо вираз парної нелінійної регресії до лінійного виду 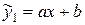 .
.
Параметри будуть обчислюватися за формулами:
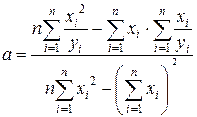 ;
;
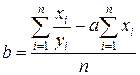 .
.
9) 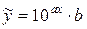 .
.
Прологарифмуємо вираз і отримаємо:
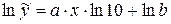 .
.
Заміною 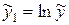 ;
; 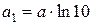 ;
; 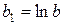 зведемо вираз до лінійного виду
зведемо вираз до лінійного виду  .
.
Параметри будуть обчислюватися за формулами:
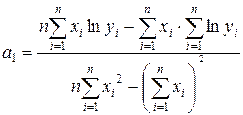 ;
;
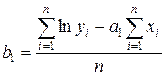 .
.
Остаточно,  ;
; 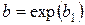 .
.
10) 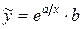 .
.
Прологарифмуємо вираз і отримаємо:
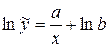 .
.
Заміною 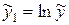 ;
; 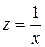 ;
; 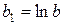 зведемо вираз до лінійного виду
зведемо вираз до лінійного виду 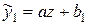 .
.
Параметри будуть обчислюватися за формулами:
 ;
;
 .
.
Остаточно 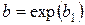 .
.
11) 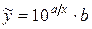 .
.
Прологарифмуємо вираз і отримаємо:
 .
.
Заміною 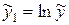 ;
; 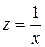 ;
; 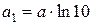 ;
; 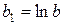 зведемо вираз до лінійного виду
зведемо вираз до лінійного виду 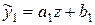 .
.
Параметри будуть обчислюватися за формулами:
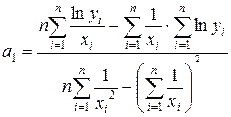 ;
;
 .
.
Остаточно,  ;
; 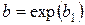 .
.
12) 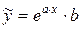 .
.
Прологарифмуємо вираз і отримаємо:
 .
.
Заміною 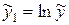 ;
; 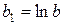 зведемо вираз парної нелінійної регресії до лінійного виду
зведемо вираз парної нелінійної регресії до лінійного виду 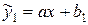 .
.
Параметри будуть обчислюватися за формулами:
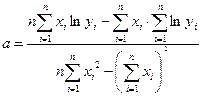 ;
;
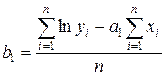 .
.
Остаточно, 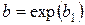 .
.
13) 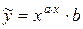 .
.
Прологарифмуємо вираз і отримаємо:
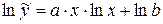 .
.
Заміною 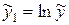 ;
; 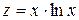
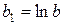 зведемо вираз до лінійного виду
зведемо вираз до лінійного виду 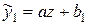 .
.
Параметри будуть обчислюватися за формулами:
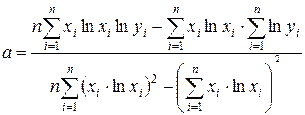 ;
;
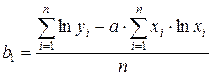 .
.
Остаточно, 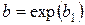 .
.
14) 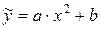
Заміною 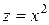 зведемо квазілінійну регресійну залежність до лінійного виду
зведемо квазілінійну регресійну залежність до лінійного виду 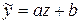 .
.
Параметри будуть обчислюватися за формулами:
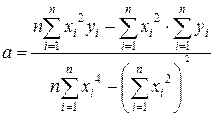 ;
;
 .
.
15) 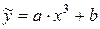
Заміною 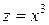 зведемо квазілінійну регресійну залежність до лінійного виду
зведемо квазілінійну регресійну залежність до лінійного виду 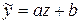 .
.
Параметри будуть обчислюватися за формулами:
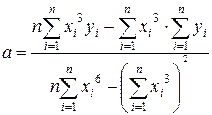 ;
;

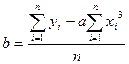 .
.
16) 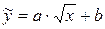
Заміною 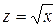 зведемо вираз квазілінійної регресійної залежності до лінійного виду
зведемо вираз квазілінійної регресійної залежності до лінійного виду 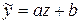 .
.
Параметри будуть обчислюватися за формулами:
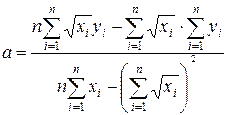 ;
;
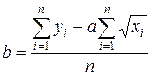 .
.
Читайте також:
- C. 3. Структурна побудова управління організаціями.
- CMM. Визначення моделі зрілості.
- I. Доповнення до параграфу про точкову оцінку параметрів розподілу
- ISO 15504.Структура еталонної моделі
- Абсолютна величина можливих значень
- Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
- Алгоритм реалізації моделі
| <== попередня сторінка | | | наступна сторінка ==> |
| ТЕМА 4. Моделі парної лінійної та нелінійної регресії | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |