• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Практичне заняття 3.

Тема заняття.Застосування похідної до доведення нерівностей.

1. Доведення умовних нерівностей з однією змінною.

1.1. Застосування достатньої умови зростання (спадання) функції до доведення умовних нерівностей з однією змінною.

1.2. Застосування достатньої умови існування екстремуму функції в точці до доведення умовних нерівностей з однією змінною.

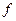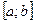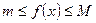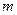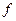1.3. Застосування правила знаходження найбільшого та найменшого значень функції на проміжку до доведення нерівностей виду , , де - найменше, - найбільше значення функції на .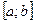

2. Доведення нерівностей з декількома змінними.

1. Доведення умовних нерівностей з однією змінною.

1.1. Застосування достатньої умови зростання (спадання) функції до доведення умовних нерівностей з однією змінною.

Теоретичний матеріал.

Умовні нерівності – це нерівності істинні на певному проміжку.

Достатня умова зростання (спадання) функції на інтервалі. Якщо в кожній точці інтервалу 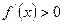( 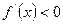), то функція зростає (спадає) на цьому інтервалі.

Якщо функція неперервна на проміжку 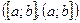і спадає (зростає) на інтервалі , то функція спадає (зростає) на проміжку .

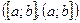Алгоритм доведення нерівностей.

1) Виходячи з умови нерівності підібрати допоміжну функцію, визначеному на вказаному в задачі проміжку.

2) Дослідити функцію на монотонність.

3) Визначивши характер монотонності записати відповідну йому нерівність за означенням зростаючої (спадної функції), або нерівність яка порівнює значення функції на проміжку з найбільшим (найменшим) значенням функції на цьому проміжку.

4) Проаналізувавши і перевіривши, якщо це потрібно, останню нерівність, зробити відповідний висновок про істинність заданої в умові задачі нерівності.

Достатня умова екстремуму. Якщо функція неперервна в точці і похідна змінює знак при переході через точку , то - точка екстремуму функції

Якщо знак змінюється з ”+” на ”-”, то - точка максимуму.

Якщо знак змінюється з ”-” на ”+”, то - точка мінімуму.

Знаходження найбільшого (найменшого) значення функції, неперервної на відрізку.

Якщо функція неперервна на відрізку і має на цьому відрізку скінченне число критичних точок, то вона набуває свого найбільшого і найменшого значення на цьому відрізку або в критичних точках, які належать цьому відрізку, або на кінцях відрізка.

Знаходження найбільшого (найменшого) значення функції, неперервної на інтервалі.

Якщо неперервна функція має на заданому інтервалі тільки одну точку екстремуму і це точка мінімуму (максимуму), то на заданому інтервалі функція набуває свого найменшого (найбільшого) значення у точці .

Приклад 1.Довести, що 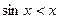для всіх .

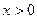Доведення.

1) Розглянемо функцію , .

2) . Отже, зростає на .

3) За означенням зростаючої функції якщ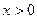о , то .

4) , .

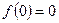Звідси .

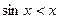
Нерівність доведено.

Приклад 2.Доведіть нерівність при .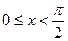

Доведення.

1) Розглянемо функцію .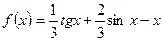

2) .

Знак похідної визначається знаком чисельника, оскільки .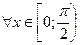

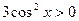2.1) Розглянемо допоміжну функцію , .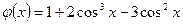

2.2) 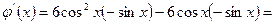на 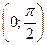. Отже, 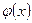зростає на .

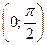В точці 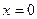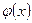неперервна, .

Тому, . Тобто (рівність можлива лише при ).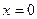

2.3) Звідси , . Отже, зростає на 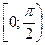, тобто . Оскільки 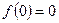, то .

3) Маємо 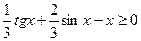. Звідси .

1.2. Застосування достатньої умови існування екстремуму функції в точці до доведення умовних нерівностей з однією змінною.

Приклад 3.Доведіть нерівність 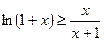, при .

Доведення.

1) Розглянемо функцію .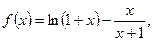

2) Дослідимо її на екстремум.

.

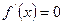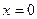при . Оскільки при переході через точку 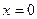похідна змінює знак з ”-” на ”+”, то за достатньою умовою екстремуму функції 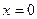- точка мінімуму.

.

Оскільки це єдина точка з інтервалу , то в ній функція досягає свого найменшого значення , , 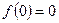тому .

3) . Звідс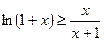и при .

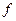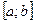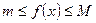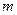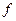1.3. Застосування правила знаходження найбільшого та найменшого значень функції на проміжку до доведення нерівностей виду , , де - найменше, - найбільше значення функції на .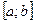

Приклад 4.Доведіть нерівність .

Доведення.

1) Нехай .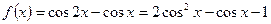

Введемо підстановку , 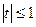. Маємо функцію , .

Функції і мають однакові області значень.

2) Знайдемо найбільше та найменше значення функції на проміжку .

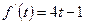. при .

Обчислимо значення функції в китичній точці та на кінцях відрізка .

Матимемо, , , .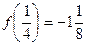

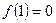Отже, , .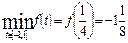

.

3) Ми одержали подвійну нерівність .

2. Доведення нерівностей з декількома змінними.

Теоретичний матеріал.

При доведенні нерівностей з декількома змінними використовують різні способи:

1) вводять допоміжну функцію, яку потім досліджують,

2) ділять нерівність на певний вираз, звівши цим самим її до нерівності з однією змінною, а потім діють за розглянутим у попередньому пункті алгоритмом,

3) вважають одну із букв змінною величиною, а значення решти букв фіксованими і при цьому діють також за вказаним алгоритмом.

Приклад 5.Відомо, що 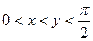. Доведіть, що .

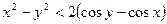Доведення.

Перенесемо доданки зі змінною 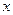в ліву сторону нерівності, а зі змінною 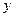у праву: .

1) Розглянемо допоміжну функцію .

2) Дослідимо її на монотонність:

.

Оскільки при (доведено у прикладі 1), то і зростає на .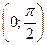

За означенням зростаючої функції якщ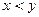о , то , тобто .

3) З останньої нерівності одержуємо 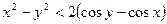, при .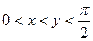

Приклад 6.Доведіть, що при , .

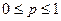
Доведення.

Поділивши обидві частини нерівності на , після певних перетворень приходимо до нерівності .

Нехай , тоді матимемо нерівність: , .

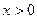1) Розглянемо допоміжну функцію , .

2) Дослідимо її на монотонність:

якщо 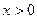, оскільки за умовою.

Отже, зростає на інтервалі . - неперервна в точці 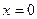, 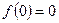. Тому коли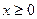 (рівність можлива лише при ).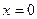

Отже, 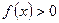, при .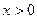

3) Маємо, . Зробивши обернену заміну та необхідні тотожні перетворення, приходимо до нерівності . Якщо , то .

Виходячи зі сказаного робимо висновок, що .

Приклад 7.Доведіть, що нерівність має місце для будь-яких додатних значень .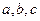

Доведення.

Вважатимемо, що .

1) Розглянемо функцію , , .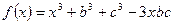

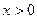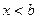2) Дослідимо її на монотонність: , то при 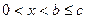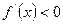. Оскільки неперервна в точці , то спадає на відрізку , звідси , тобто . (1)

3) Розглянемо другу функцію , , 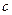- фіксоване число.

4) Дослідимо 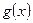на монотонність: . При . Оскільки 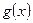неперервна в точці , то 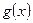спадає на відрізку , звідси 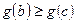, тобто 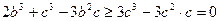. Отже,

. (2)

З (1) і (2) за властивістю транзитивності маємо: .

5) Отже, . Підставивши замість 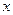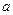, одержуємо нерівність яку слід було довести.

Читайте також:

1. II. Основна частина ЗАНЯТТЯ
2. III. Підсумок ЗАНЯТТЯ
3. IV ПІДСУМОК ЗАНЯТТЯ.
4. IV ПІДСУМОК ЗАНЯТТЯ.
5. IV. Підсумок ЗАНЯТТЯ
6. IV. Підсумок ЗАНЯТТЯ
7. IV. Підсумок ЗАНЯТТЯ
8. IV. Підсумок ЗАНЯТТЯ
9. IV. Підсумок ЗАНЯТТЯ
10. IV. Підсумок ЗАНЯТТЯ
11. IV. Підсумок ЗАНЯТТЯ
12. IV. Підсумок ЗАНЯТТЯ

Переглядів: 449